Если сила перпендикулярна оси, то её проекция на эту ось равна нулю.
Пример: Вычислить проекции силы 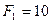 кН на координатные оси х и y (рис. 2.10), если заданная сила
кН на координатные оси х и y (рис. 2.10), если заданная сила  образует угол 30° с положительным направлением оси х и угол 60° с отрицательным направлением оси у.
образует угол 30° с положительным направлением оси х и угол 60° с отрицательным направлением оси у.
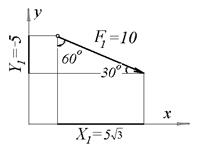
Рис.2.10
Используя приведенные выше определения, найдем:
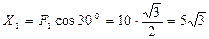 кН;
кН;
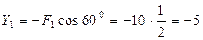 кН.
кН.
Процесс определения проекций силы на две взаимно перпендикулярные оси совпадает с разложением силы по этим осям. С другой стороны величина и направление силы могут быть найдены, если известны её проекции на две взаимно перпендикулярные оси.
Пусть известны проекции 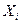 и
и 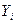 некоторой силы
некоторой силы 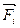 , приложенной к телу в точке А (рис.2.8) и требуется найти величину и направление силы
, приложенной к телу в точке А (рис.2.8) и требуется найти величину и направление силы 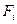 . Из концов проекций восстановим перпендикуляры к осям и продолжим их до взаимного пересечения в точках A,B,B1 и B2. Диагональ АВ полученного прямоугольника определяет искомую силу
. Из концов проекций восстановим перпендикуляры к осям и продолжим их до взаимного пересечения в точках A,B,B1 и B2. Диагональ АВ полученного прямоугольника определяет искомую силу 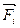 .
.
Если проекции силы имеют положительные знаки, то сила образует острые углы с положительными направлениями осей координат. Модуль силы 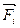 легко определить из треугольника АВВ1 по теореме Пифагора:
легко определить из треугольника АВВ1 по теореме Пифагора:
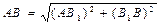 или
или 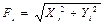 (2.15)
(2.15)
Направление силы 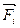 определяется по косинусам углов
определяется по косинусам углов 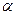 и
и 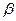 между этой силой и координатными осями. Из треугольников АВВ1 и АВВ2 следует:
между этой силой и координатными осями. Из треугольников АВВ1 и АВВ2 следует:
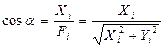 и
и 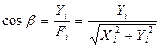 (2.16)
(2.16)
Дата добавления: 2018-11-26; просмотров: 1968;











