Равнодействующая двух сил, приложенных в одной точке. Параллелограмм сил.

Система сил, линии действия которых пересекаются в одной точ­ке, называется системой сходящихся сил.

Простейшую систему сходящихся сил образуют две силы, приложенные к телу в одной точке. Согласно третьей аксиоме статики их равнодействующая выражается диагональю параллелограмма, построен­ного на заданных силах и называемого параллелограммом сил. Прави­ло нахождения равнодействующей называется правилом параллелограм­ма. Существуют два способа определения величины и направления равнодействующей двух сил: графический и аналитический. Рассмот­рим последовательно каждый из них.

Пусть в точке А твердого тела приложены две силы и , линии действия которых образуют угол α. Вычертим в выбранном масштабе заданные силы (рис.2.1,а) и построим на них параллелограмм АВСD. Диагональ АС этого параллелограмма определяет равнодействую­щую 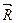заданных сил по величине и направлению. Модуль равнодействую­щей определяется путем измерения диагонали АС в масштабе сил, а её направление - путем измерения угла βмежду равнодействующей 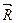. и силой , либо угла γ между равнодействующей 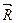иси­лой .

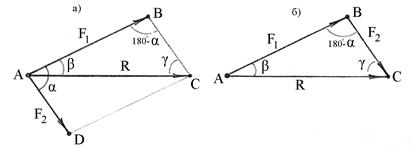
Рис.2.1

Рассмотрим треугольник ABC. Сторона АВ этого треугольника равна силе , сторона ВС геометрически равна силе , а сторо­на АС является равнодействующей двух заданных сил. Отсюда следует, что равнодействующая двух сил может быть определена по правилу треугольника сил. Для построения этого треугольника необходимо из конца В силы отложить вектор, геометрически равный силе , т.е. вектор той же длины, что и сила , параллельный ей и направленный в ту же сторону. Замыкающий вектор, проведенный из начала силы в конец силы является равнодействующей двух заданных сил (рис.2.1,б).

Следует обратить внимание на то обстоятельство, что стороны треугольника, представляющие заданные силы, всегда имеют одно направление (по ходу часовой стрелки или противоположно), в то время как равнодействующая имеет противоположное им направление, т.е. замыкает силовой треугольник.

Для определения равнодействующей двух сил аналитическим спо­собом следует построить силовой треугольник схематически, т.е. без соблюдения масштаба сил, и определить модуль и направление равнодействующей из решения силового треугольника.

Так, например, для определения модуля равнодействующей 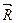двух сил и , представленных на рис.2.1,б, воспользуемся теоремой косинусов. Учитывая, что угол ABC силового треугольника равен 180°-α, запишем следующее выражение на основании теоремы косинусов:

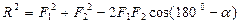, так как 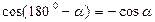, получим:

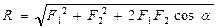(2.1)

По формуле (2.I) вычисляется модуль равнодействующей двух сил, линии действия которых образуют между собой произвольный угол α.

Для определения направления равнодействующей 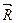по отноше­нию к заданным силам, т.е. для определения углов β и γ между линией действия равнодействующей 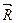и линиями действия заданных сил и , воспользуемся теоремой синусов:

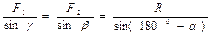
Учитывая, что 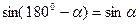, получим

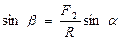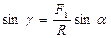и (2.2)

В некоторых частных случаях расположения заданных сил формулы (2.I) и (2.2), определяющие модуль и направление равнодействующей, мо­гут быть упрощены. Рассмотрим следующие частные случаи:

I. Силы и не равны по модулю и образуют прямой угол (рис.2.2,а)

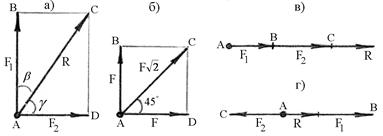
Рис. 2.2

В этом случае имеем: 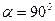, 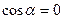и 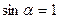. После подстановки этих значений в формулы (2.I) и (2.2), получим:

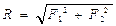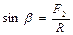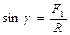, и (2.3)

2. Силы и равны по модулю и образуют прямой угол (рис.2.2,6).

Обозначим модуль сил символом 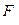и воспользуемся выражениями (2.3). В результате получим:

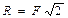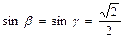, , (2.4)

Следовательно, равнодействующая двух равных и взаимно перпендикулярных сил равна модулю одной из сил, умноженному на 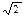и образует углы равные 45⁰ из каждой силой.

3. Силы и не равны по модулю и направлены вдоль общей прямой в одну сторону (рис.2.2,в). В этом случае:

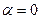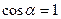, и 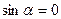, следовательно:

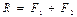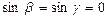, , т.е. 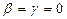(2.5)

Итак, равнодействующая двух сил, приложенных в одной точке и направленных вдоль общей прямой в одну сторону, равна сумме этих сил и направлена в ту же сторону, что и заданные силы.

4. Силы и направлены вдоль общей прямой в противопо­ложные стороны (рис.2.2,г). В этом случае угол 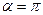, 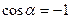и 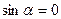. Тогда по формуле (2.I) находим:

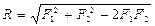(2.6)

Из выражения (2.6) вытекают, что равнодействующая зависит от соотношения модулей заданных сил. Возможны следующие три соотношения:

а) 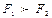, тогда 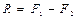(2.7)

б) 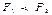, тогда 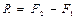(2.8)

в) 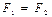, тогда 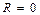(2.9)

Таким образом, равнодействующая двух сил, направленных вдоль общей прямой в противоположные стороны равна разности этих сил. Направление равнодействующей совпадает с направлением силы, имеющей больший модуль.

Равнодействующая двух равных и противоположно направленных сил равна нулю (аксиома I).

2.2. Разложение силы на две составляющие.

Задача сложения сил, рассмотренная в предыдущем параграфе, позволяет заменить действие системы сил на тело одной равнодейст­вующей. К такой замене часто прибегают в технической механике с целью упрощения решения практических задач.

Иногда возникает необходимость решения обратной задачи, сос­тоящей в разложении заданной силы на две составляющие. Такое разло­жение может быть выполнено по правилу параллелограмма, так как лю­бая сила может рассматриваться как равнодействующая двух сходящих­ся сил. Очевидно, что множество параллелограммов могут иметь одну и ту же диагональ. Следовательно, задача разложения силы на две составляющие имеет множество решений. Для получения конкретного, определенного разложения силы необходимо задать дополнительные ус­ловия, которые конкретизируют два параметра составляющих сил. Отсюда вытекает, что определенное разложение силы на две составля­ющие может быть получено:

а) если известны линии действия двух составляющих;

б) если заданы линия действия одной составля­ющей и модуль другой;

в) если известны модули двух составляющих;

г) если известны модуль и линия действия одной из состав­ляющих.

Рассмотрим последовательность разложения заданной силы при указанных условиях.

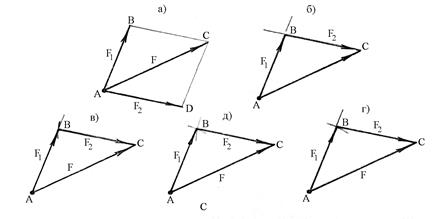
Рис.2.3

Пусть задана сила 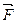и линии действия её составляющих и . В выбранном масштабе вычертим вектор 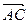геометрически равный силе 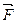(рис.2.3а). Из начала и конца этого вектора (точек А и С соответственно) проведем прямые линии, параллельно линиям действия сос­тавляющих сил и до взаимного их пересечения в точках В и D. В результате получим параллелограмм сил АВСD, стороны АВ и АD которого геометрически равны искомым силам и .

Решение этой же задачи можно выполнить по правилу силового треугольника. Для этого необходимо из начала заданной силы 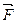(точки А) провести прямую параллельно линии действия одной составляющей, а из её конца (точки С) - прямую параллельно линии действия другой составляющей. В пересечении этих прямых получаем точку В (рис.2.3,6). Величины составляющих определяются измерением сторон АВ и ВС тре­угольника сил АВС в принятом масштабе, а их направления устанавли­ваются против направления заданной силы по обводу треугольника.

Если заданы линия действия одной составляющей и модуль другой, то разложение заданной силы 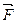осуществляется следующим образом: Из начала А силы 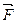(рис.2.3,в) проводим прямую параллельно заданной линии действия одной составляющей. Затем из конца С силы 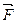как из центра, раствором циркуля равным модулю другой составляющей, проводим дугу окружности до пересечения с ранее проведенной прямой в точке В. Точки В и С соединяем и получаем силовой треугольник ABC. Величины и направления составляющих определяются так, как и в первом случае.

Разложение силы 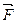на составляющие и , модули кото­рых известны, производится в такой последовательности:

- вычерчи­вается заданная сила 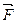в некотором масштабе

- из начала этой силы (из точки А) описывается дуга окружности, радиус которой равен модулю одной из составляющих, а из конца заданной силы (из точ­ки С) описывается вторая дуга окружности, радиус которой равен мо­дулю другой составляющей (рис.2.3,д). Точка пересечения этих дуг соединяется с началом и концом заданной силы. Полученный таким образом силовой треугольник ABC позволяет определить ве­личины и направления искомых составляющих и .

Возможен второй вариант разложения силы 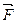на две составляю­щие, модули которых известны. Предлагаем учащимся установить этот вариант разложения силы в качестве упражнения.

Для нахождения составляющих и силы 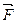по известным модулю и линии действия одной из них необходимо из начала силы 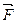(из точки А) провести прямую, параллельно линии действия заданной сос­тавляющей и отложить на ней отрезок АВ численно равный модулю этой составляющей. Если соединить точку В с концом заданной силы, то образуется силовой треугольник ABC (рис.2.3,г), сторона ВС которого определяет вторую искомую составляющую по величине и направлению.