Теоремы о сложении двух параллельных сил.
Теорема I. Равнодействующая двух параллельных сил, направленных в одну сторону, равна их сумме, направлена в ту же сторону, параллельна им и приложена в точке, которая делит расстояние между заданными силами на части, обратно пропорциональные их модулям.
Для доказательства этой теоремы рассмотрим две параллельные силы  и
и 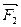 , приложенные соответственно в точках А и В твердого тела и направленные в одну сторону (рис.3.1). Соединим точки приложения заданных сил и вдоль этой прямой приложим в точках А и В соответственно силы
, приложенные соответственно в точках А и В твердого тела и направленные в одну сторону (рис.3.1). Соединим точки приложения заданных сил и вдоль этой прямой приложим в точках А и В соответственно силы 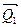 и
и 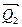 равные по модулю и противоположные по направлению. Приложение таких сил не нарушает характера действия заданных сил на твердое тело. Пользуясь правилом геометрического сложения сил, найдем равнодействующие
равные по модулю и противоположные по направлению. Приложение таких сил не нарушает характера действия заданных сил на твердое тело. Пользуясь правилом геометрического сложения сил, найдем равнодействующие 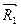 и
и 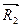 сил, приложенных в точках А и В.
сил, приложенных в точках А и В.
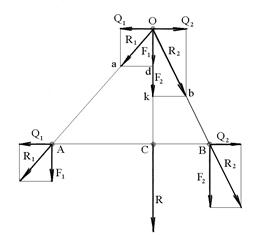
Рис.3.1
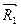 =
=  +
+ 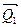 и
и 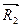 =
= 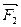 +
+ 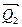 .
.
Из рисунка 3.1 видно, что линии действия сил 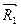 и
и 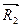 пересекаются в точке О.
пересекаются в точке О.
Перенесем эти силы в точку О и разложим их на исходные составляющие  ,
, 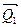 и
и 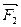 ,
, 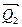 . Составляющие
. Составляющие 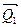 и
и 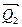 равные по модулю и направленные вдоль горизонтальной прямой в противоположные стороны, взаимно уравновешиваются, а составляющие
равные по модулю и направленные вдоль горизонтальной прямой в противоположные стороны, взаимно уравновешиваются, а составляющие  и
и 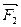 действуют вдоль общей вертикальной прямой в одном направлении. Равнодействующая таких сил равна их алгебраической сумме и направлена вдоль линии их действия в ту же сторону, т.е:
действуют вдоль общей вертикальной прямой в одном направлении. Равнодействующая таких сил равна их алгебраической сумме и направлена вдоль линии их действия в ту же сторону, т.е:
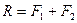 (3.1)
(3.1)
Перенесем равнодействующую 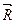 в точку С, расположенную на прямой АВ и рассмотрим подобие образовавшихся треугольников:
в точку С, расположенную на прямой АВ и рассмотрим подобие образовавшихся треугольников:
Треугольник АОС подобен треугольнику аОd, а треугольник ОВС подобен треугольнику Оbk. Составим отношения их сторон:
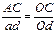 и
и 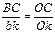
Откуда 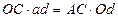 и
и 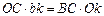 , но
, но 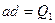 , а
, а 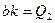 , следовательно, левые части последних двух равенств одинаковы. Приравнивая правые части этих равенств, получаем:
, следовательно, левые части последних двух равенств одинаковы. Приравнивая правые части этих равенств, получаем:
 , где
, где 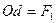 , а
, а 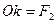 . Тогда:
. Тогда:
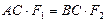 , откуда
, откуда 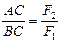 (3.2)
(3.2)
Таким образом, точка приложения равнодействующей делит расстояние АВ между точками приложения заданных сил на отрезки АС и ВС обратно пропорциональные модулям этих сил.
Теорема 2. Равнодействующая двух параллельных, не равных по модулю и противоположно направленных сил, равна их разности, направлена параллельно этим силам в сторону большей из них и приложена на продолжении прямой, соединяющей точки приложения заданных сил в точке, расстояния которой от точек приложения заданных сил обратно пропорциональны их модулям.
Пусть в точках А и В некоторого твердого тела приложены две параллельные силы  и
и 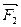 , направленные в противоположные стороны. Положим, что
, направленные в противоположные стороны. Положим, что 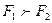 (рис.3.2).
(рис.3.2). 
Разложим силу  на две параллельные ей составляющие
на две параллельные ей составляющие 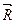 и
и 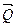 , направленные в одну сторону и приложенные в точках С и В соответственно. (Точка С взята на продолжении отрезка ВА, но её положение пока неизвестно). Модуль составляющей
, направленные в одну сторону и приложенные в точках С и В соответственно. (Точка С взята на продолжении отрезка ВА, но её положение пока неизвестно). Модуль составляющей 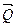 принимаем равным модулю заданной силы
принимаем равным модулю заданной силы 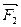 , тогда модуль силы
, тогда модуль силы 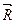 , приложенной в точке С определится разностью
, приложенной в точке С определится разностью 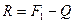 , или
, или
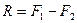 (3.3)
(3.3)
Силы 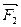 и
и 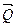 взаимно уравновешиваются, так как они равны по модулю, приложены в одной точке и направлены вдоль общей прямой в противоположные стороны. Следовательно, сила
взаимно уравновешиваются, так как они равны по модулю, приложены в одной точке и направлены вдоль общей прямой в противоположные стороны. Следовательно, сила 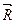 является равнодействующей двух заданных сил
является равнодействующей двух заданных сил  и
и 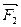 . Модуль равнодействующей
. Модуль равнодействующей 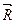 определяется по формуле (3.3), а точка её приложения находится на продолжении отрезка ВА со стороны большей силы.
определяется по формуле (3.3), а точка её приложения находится на продолжении отрезка ВА со стороны большей силы.
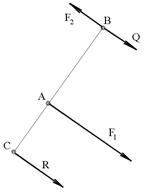
Рис.3.2
Принимая во внимание, что сила  является равнодействующей двух параллельных и направленных в одну сторону сил
является равнодействующей двух параллельных и направленных в одну сторону сил 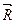 и
и 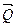 , на основании пропорции (3.2) можем записать:
, на основании пропорции (3.2) можем записать:
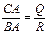 , или
, или 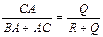 , но
, но
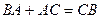 ,
, 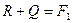 ,
, 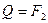 , следовательно:
, следовательно:
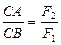 (3.4)
(3.4)
Таким образом, расстояния от точки приложения равнодействующей до точек приложения заданных сил обратно пропорциональны модулям этих сил.
Дата добавления: 2018-11-26; просмотров: 2434;











