Уравнения равновесия плоской системы сходящихся сил.
Рассмотрим систему сил  ,
, 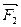 ,
, 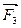 …
… 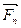 , приложенных к телу в точке А (рис.2.11). Построим многоугольник сил ABC...К, замыкающая сторона которого определяет равнодействующую заданных сил по модулю и направлению, т.е. вектор
, приложенных к телу в точке А (рис.2.11). Построим многоугольник сил ABC...К, замыкающая сторона которого определяет равнодействующую заданных сил по модулю и направлению, т.е. вектор 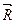 . Проведем две взаимно перпендикулярные оси х и у . Опустим перпендикуляры к этим осям из всех вершин многоугольника сил (рис.2.11). Отрезки осей, заключенные между проведенными перпендикулярами, являются проекциями заданных сил и их равнодействующей на соответствующие координатные оси.
. Проведем две взаимно перпендикулярные оси х и у . Опустим перпендикуляры к этим осям из всех вершин многоугольника сил (рис.2.11). Отрезки осей, заключенные между проведенными перпендикулярами, являются проекциями заданных сил и их равнодействующей на соответствующие координатные оси.
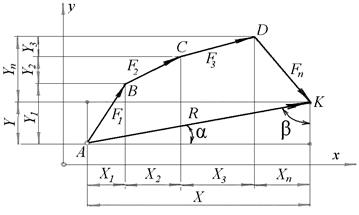
Рис.2.11
Из рис.2.11 следует:
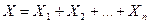 или
или 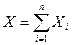 (2.17)
(2.17)
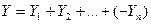 или
или 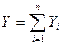 (2.18)
(2.18)
В выражениях (2.17) и (2.18) проекции сил могут быть положительными, отрицательными или равными нулю в зависимости от величин углов между заданными силами и координатными осями.
Итак, проекция равнодействующей системы сходящихся сил на любую координатную ось равна алгебраической сумме проекций всех заданных сил на ту же ось.
Модуль и направление равнодействующей определяются через её проекции X и Y по формулам, полученным в предыдущем параграфе для одной силы:
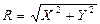 ;
; 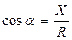 ;
; 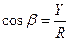 (2.19)
(2.19)
Если система сходящихся сил находится в равновесии, то модуль её равнодействующей 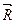 равен нулю: R=0. Это равенство возможно только в том случае, когда каждое из слагаемых подкоренного выражения (2.19) одновременно равно нулю, т.е.
равен нулю: R=0. Это равенство возможно только в том случае, когда каждое из слагаемых подкоренного выражения (2.19) одновременно равно нулю, т.е.
X = 0 и Y = 0.
После подстановки этих значений в выражения (2.17 и 2.18) получим аналитические условия равновесия системы сходящихся сил:
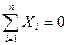 ;
; 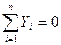 (2.20)
(2.20)
Таким образом, для равновесия плоской системы сходящихся сил необходимо и достаточно, чтобы алгебраические суммы проекций всех сил на любые две взаимно перпендикулярные оси одновременно были равными нулю.
Уравнения равновесия вытекают из условий (2.20), если левые их части расписать как суммы проекций всех сил, действующих на тело в одной точке, или сил, линии действия которых пересекаются в одной точке. Эти уравнения имеют вид:
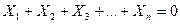 (2.21)
(2.21)
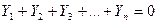 (2.22)
(2.22)
Уравнения равновесия позволяют определить модуль и направление одной неизвестной силы заданной системы, либо величины двух сил, направления которых заданы. В следующем параграфе рассматриваются примеры, решение которых осуществляется с использованием уравнений равновесия.
2.7 Типовые задачи и методика их решения.
Основные задачи статики твердого тела, нагруженного плоской системой сходящихся сил, можно разделить на две группы:
1. Задачи на равновесие тел под действием трех сил;
2. Задачи на равновесие тел под действием произвольного числа сил, линии действия которых пересекаются в одной точке.
Решение задач первой группы сводится к разложению заданной силы на две составляющие по заданным направлениям и может быть получено графическим (геометрическим), или аналитическим приемами. Для этого необходимо:
а) установить и показать на чертеже линии действия всех сил, приложенных к твердому телу;
б) построить силовой треугольник в выбранном масштабе сил при графическом решении задачи, или схематически, без соблюдения масштаба, при аналитическом решении задачи;
в) определить направления искомых сил так, чтобы стрелки всех сторон силового треугольника были направлены в одном порядке (при обходе контура треугольника, стрелки всех его сторон должны быть направлены по ходу часовой стрелки или противоположно);
г) определить модули искомых сил путем измерения соответствующих сторон силового треугольника в принятом масштабе, либо путем решения этого треугольника по теореме синусов.
Пример 2.1. Определить натяжение Т нити АС и усилие N в стержне АВ, вызванные действием груза G= 10 кН (рис.2.12,а).
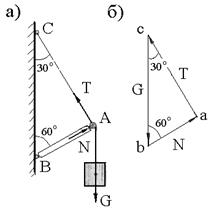
Рис.2.12
Решение данного примера выполним двумя приемами: графическим и аналитическим.
Графический прием. Задаемся масштабом сил 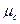 =0,25 кН/мм и откладываем по вертикали отрезок cb, длина которого равна 40 мм cb = G:
=0,25 кН/мм и откладываем по вертикали отрезок cb, длина которого равна 40 мм cb = G: 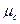 = 10 : 0,25 = 40 мм. Полученный вектор
= 10 : 0,25 = 40 мм. Полученный вектор 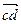 геометрически равен действующей силе
геометрически равен действующей силе 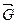 . Так как натяжение нити
. Так как натяжение нити 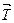 и усилие
и усилие 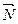 в стержне АВ направлены вдоль их геометрических осей, то для построения силового треугольника достаточно провести из точки с прямую параллельно нити АС, а из точки b - прямую параллельно стержню АВ. Построенный силовой треугольник аbс позволяет определить величины и направления искомых сил. Измерив стороны: ас и bа силового треугольника в принятом масштабе, получаем:
в стержне АВ направлены вдоль их геометрических осей, то для построения силового треугольника достаточно провести из точки с прямую параллельно нити АС, а из точки b - прямую параллельно стержню АВ. Построенный силовой треугольник аbс позволяет определить величины и направления искомых сил. Измерив стороны: ас и bа силового треугольника в принятом масштабе, получаем:
Т = 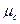 ∙ас = 0,25∙34,5 = 8,6 кН ; N=
∙ас = 0,25∙34,5 = 8,6 кН ; N= 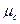 ∙bа = 0,25∙20 = 5 кН.
∙bа = 0,25∙20 = 5 кН.
Направления искомых сил находим в соответствии с условием равновесия системы трех сил. Используя это условие и учитывая, что заданная сила 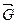 направлена вниз, устанавливаем направления искомых сил (рис.2.12,б).
направлена вниз, устанавливаем направления искомых сил (рис.2.12,б).
Аналитический прием. Вычертим схематически силовой треугольник сbа (рис.2.12,б) так, чтобы его стороны были параллельны заданной силе G. и искомым силам 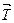 и
и 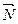 . В полученном треугольнике известна сторона cb = G, = 10 кH и известны величины всех углов. Поэтому модули искомых усилий
. В полученном треугольнике известна сторона cb = G, = 10 кH и известны величины всех углов. Поэтому модули искомых усилий 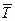 и
и 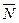 ,соответственно равные сторонам ас и bа силового треугольника, легко определяются по теореме синусов:
,соответственно равные сторонам ас и bа силового треугольника, легко определяются по теореме синусов:
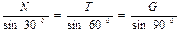 , откуда находим:
, откуда находим:
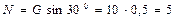 кН,
кН,
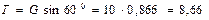 кН.
кН.
Направления искомых сил определяются таким же образом, как и при графическом приеме решения задачи.
Пример 2.2. Груз G = 25 кН подвешен в точке А при помощи двух тросов, образующих между собой угол 120° (рис.2.13,а). Требуется определить модули натяжений 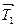 и
и 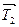 тросов.
тросов.
Решение с использованием графического приема. Заданная сила 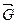 и искомые натяжения
и искомые натяжения 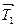 и
и 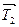 , направленные вдоль геометрических осей тросов, взаимно уравновешиваются. Для построения силового треугольника выбираем масштаб сил
, направленные вдоль геометрических осей тросов, взаимно уравновешиваются. Для построения силового треугольника выбираем масштаб сил 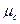 = I кН/мм и откладываем отрезок od = 25 мм, параллельный заданной силе
= I кН/мм и откладываем отрезок od = 25 мм, параллельный заданной силе  (рис.2.13,б).
(рис.2.13,б).
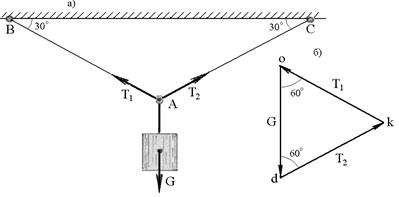
Рис.2.13
Из точек о и d проводим прямые, параллельные искомым силам и продолжаем их до взаимного пересечения в точке k. Стороны dk и kо полученного треугольника сил геометрически равны неизвестным натяжениям тросов. Из рис.25,б следует, что построенный силовой треугольник является равносторонним. Поэтому
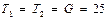 кН.
кН.
Направления этих сил показаны на рис.2.13,а и 2.13,б. Они устанавливаются на основании геометрического условия равновесия системы сходящихся сил.
Аналитический прием решения. Строим схематически треугольник сил odk рис.2.13,б). Устанавливаем величины углов этого треугольника и на основании теоремы синусов находим:
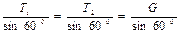 , откуда имеем
, откуда имеем 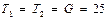 кН.
кН.
Пример 2.3. Балка на двух шарнирных опорах загружена силой F = 30 кн (рис.2.14,а). Требуется определить реакции опор балки.
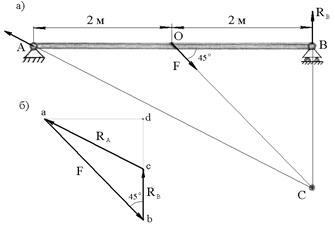
Рис.2.14
Графический прием решения. Балка АВ находится в равновесии под действием трех сил: заданной силы 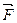 и неизвестных реакций опор
и неизвестных реакций опор 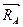 и
и 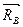 . Так как опора В горизонтально подвижная, то её реакция
. Так как опора В горизонтально подвижная, то её реакция 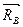 действует вертикально вверх. Продолжим линии действия сил
действует вертикально вверх. Продолжим линии действия сил 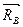 и
и 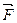 до пересечения их в точке С. Согласно теореме о трех силах, линия действия реакции
до пересечения их в точке С. Согласно теореме о трех силах, линия действия реакции 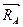 проходит через полученную точку С (рис.2.14,а).
проходит через полученную точку С (рис.2.14,а).
Выбираем масштаб сил 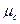 = I кН/мм и строим силовой треугольник аbс (рис.276), стороны ас и bс которого геометрически равны искомым реакциям опор. Измерим указанные стороны треугольника в принятом масштабе, получаем:
= I кН/мм и строим силовой треугольник аbс (рис.276), стороны ас и bс которого геометрически равны искомым реакциям опор. Измерим указанные стороны треугольника в принятом масштабе, получаем:
RA = 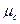 ∙23,7 = 23,7 кН ; RВ =
∙23,7 = 23,7 кН ; RВ = 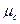 ∙10,6 = 10,6 кН .
∙10,6 = 10,6 кН .
Направления реакций опор устанавливаются так, чтобы треугольник сил был замкнут (рис.2.14,б).
Аналитический прием решения. Строим схематически силовой треугольник аbс и устанавливаем величины углов между его сторонами: 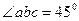 ;
; 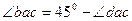 ,
,
но 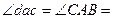 26°36/ (т.к.
26°36/ (т.к. 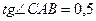 ). Тогда
). Тогда
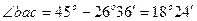 и
и 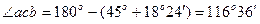
Воспользуемся теоремой синусов:
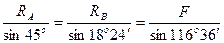 , откуда
, откуда
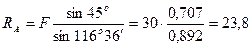 кН;
кН;
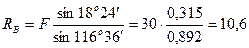 кН.
кН.
Решение задач второй группы сводится к определению реакций связей загруженного тела и, как правило, выполняется аналитическим способом при использовании условий равновесия. При этом решение задачи рекомендуется осуществлять в такой последовательности:
а) установить и показать на чертеже все силы, действующие на
тело, равновесие которого изучается;
б) выбрать рациональные направления координатных осей и записать два условия равновесия плоской системы сходящихся сил;
в) составить уравнения равновесия и из их решения найти значения неизвестных сил, т.е. реакций связей рассматриваемого тела.
Пример 2.4. Шар, вес которого равен 60 Н, подвешен с помощью гибкой нити АВ и опирается на гладкую наклонную плоскость в точке С. Требуется определить модули натяжения нити Т и реакции наклонной плоскости T , если шар загружен горизонтальной силой F = 10 Н, линия действия которой проходит через центр шара (рис.2.15,а).
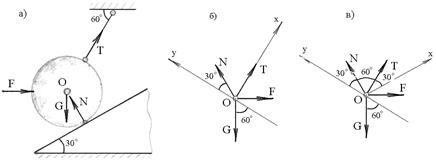
Рис.2.15
Решение. Рассматриваемый шар находится в равновесии под действием четырех сил, показанных на рис.2.15а. Так как линии действия всех сил пересекаются в центре О шара, то вместо шара можно рассматривать равновесие точки О под действием тех же сил (рис.2.15,б).
Выбираем оси проекций так, чтобы одна из них была перпендикулярна к одному из определяемых усилий, например ось y перпендикулярна силе 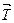 (рис.2.15,б), и записываем условия равновесия:
(рис.2.15,б), и записываем условия равновесия:
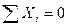 и
и 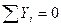
Составляем уравнения равновесия, суммируя проекции всех сил на выбранные координатные оси хи у:
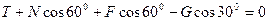 (2.23)
(2.23)
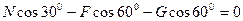 (2.24)
(2.24)
Из уравнения (2.24) находим реакцию наклонной плоскости:
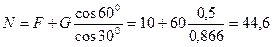 Н.
Н.
Натяжение нити Т определяем из уравнения (2.23):
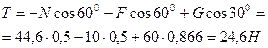
В результате получены положительные значения модулей сил 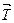 и
и 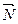 . Это означает, что предварительно выбранные их направления верны. Если при решении уравнений будет получено отрицательное значение некоторой реакции, то её истинное направление противоположно предварительно выбранному направлению, показанному на чертеже. В таком случае следует исправить направление реакции, а её модуль считать положительным.
. Это означает, что предварительно выбранные их направления верны. Если при решении уравнений будет получено отрицательное значение некоторой реакции, то её истинное направление противоположно предварительно выбранному направлению, показанному на чертеже. В таком случае следует исправить направление реакции, а её модуль считать положительным.
Примечание: Плоская система сходящихся сил находится в равновесии, если одновременно равны нулю алгебраические суммы проекций всех сил на любые две координатные оси. Это означает, что при решении задач не обязательно выбирать систему взаимно перпендикулярных осей проекций. Рациональнее выбрать оси проекций так, чтобы каждая из них была перпендикулярна одному из определяемых неизвестных усилий. В этом случае каждое уравнение равновесия будет содержать только одну неизвестную и исключается необходимость совместного решения системы алгебраических уравнений.
Вернемся к решению примера 4. Направим ось х - перпендикулярно неизвестной силе 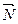 , а ось у- перпендикулярно силе
, а ось у- перпендикулярно силе 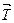 (рис.27,в). Тогда уравнение (2.23) не изменится и его решение позволяет найти модуль силы
(рис.27,в). Тогда уравнение (2.23) не изменится и его решение позволяет найти модуль силы 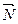 (
( 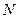 = 44,6 Н) , а вместо уравнения (2.24) получим:
= 44,6 Н) , а вместо уравнения (2.24) получим:
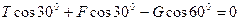 , откуда
, откуда
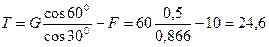 Н,
Н,
что совпадает с полученным ранее значением силы 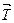 .
.
Вопросы для самоконтроля полученных знаний.
1) Какими способами можно определить равнодействующую двух сил, приложенных в одной точке тела?
2) Объясните сущность графического способа определения равнодействующей двух сил, приложенных в одной точке тела.
3) Как определяется величина равнодействующей двух сил, приложенных в одной точке тела, при использовании аналитического способа?
4) Как определяется направление равнодействующей двух сил, приложенных в одной точке тела, при использовании аналитического способа?
5) Чему равна равнодействующая двух равных по модулю сил, приложенных в одной точке тела, если их линии действия образуют прямой угол? Чему равны в этом случае углы между равнодействующей и заданными силами?
6) Чему равна равнодействующая двух сил, направленных вдоль общей прямой линии в одну сторону?
7) Чему равна равнодействующая двух сил, направленных вдоль общей прямой линии в разные стороны?
8) Как осуществляется разложение силы на две составляющие, если известны линии действия этих составляющих?
9) Как осуществляется разложение силы на две составляющие, если известна линия действия одной составляющей и модуль другой составляющей?
10) Как осуществляется разложение силы на две составляющие, если известны модули этих составляющих?
11) Как осуществляется разложение силы на две составляющие, если известны модуль и линия действия одной их составляющих?
12) Что такое система сходящихся сил на плоскости?
13) Чему равна равнодействующая плоской системы сходящихся сил? Приведите пример геометрического сложения трех сил, приложенных в одной точке тела.
14) В каком случае система сходящихся сил находится в равновесии?
15) Что такое проекция силы на ось? Как она определяется?
16) Может ли проекция силы на ось быть равной нулю? Если может, то, в каком случае?
17) Может ли проекция силы на ось иметь отрицательный знак? Если может, то, в каком случае?
18) Как осуществляется разложение силы по координатным осям?
19) Как определить величину и направление силы, если известны её проекции на две взаимно перпендикулярные оси координат? Приведите формулы определения модуля равнодействующей и углов между линией её действия и координатными осями.
20) Запишите условия равновесия плоской системы сходящихся сил.
21) Как составить уравнения равновесия плоской системы сходящихся сил?
22) Что можно определить из уравнений равновесия?
ГЛАВА III
Дата добавления: 2018-11-26; просмотров: 2899;











