Теорема о трех силах.

Теорема: Если под действием трех не параллельных сил твердое тело находится в равновесии, то линии действия этих сил пересекаются в одной точке.

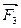Положим, что некоторое твердое тело (рис.2.6) находится в равновесии под действием трех сил , и , приложенных соответ­ственно в точках А, В и С.

Продолжим линии действия сил и 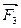до взаимного их пере­сечения в точке О и перенесем в эту точку указанные силы. Найдем равнодействующую 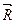сил и 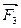по правилу параллелограмма. После замены действия сил и 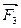их равнодействующей 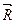,тело будет находиться в равновесии под действием двух сил и 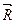, что возможно лишь в том случае, когда эти силы равны по модулю и дей­ствуют вдоль общей прямой в противоположные стороны. Следовательно, линия действия третьей силы также проходит через точку О, что и требовалось доказать.

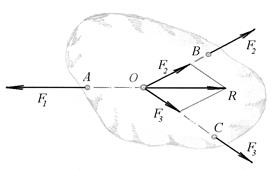
Рис.2.6

Необходимо иметь в виду, что обратное утверждение не справедливо. Если линии действия трех сил пересекаются в одной точке, то это не является признаком или условием их равновесия.

Проекция силы на ось. Разложение силы по

Координатным осям.

Проекцией заданной силы 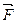на произвольную ось называется отрезок этой оси, взятый со знаком плюс пли минус и заключенный между двумя перпендикулярами, проведенными к оси через начало и конец силы.

Рассмотрим силу 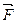, образующую с горизонтальной осью xугол α и найдем её проекцию на эту ось (рис.2.7).

Через начало А, и конец В заданной си­лы проведем перпендикуляры к оси xи обозначим точки их пересече­ния с осью через a и b. Согласно приведенному выше определению отрезок ab является проекцией силы 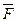на ось x. Обозначим её символом X , т.е. ab = X.

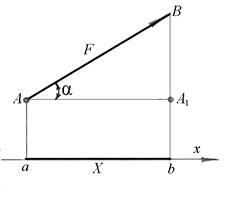
Рис.2.7

Из начала силы 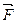проведем прямую АА₁ параллельно оси x. В результате получим прямоугольный треу­гольник ABA₁, гипотенуза которого равна заданной силе 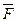, а катет АА₁ равен проекции этой силы на ось x, т.е. АА₁ = X. Из треуголь­ника ABA₁ следует:

АА₁= AB∙cosα , или

X = 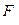cosα (2.11)

Угол α всегда измеряется от положительного направления оси к положительному направлению силы.

Таким образом, проекция силы на ось равна произведению модуля силы на косинус угла, заключенного между положительными направле­ниями силы и оси.

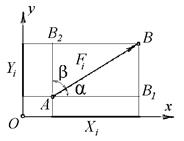
Рис.2.8

Проекция силы на ось обозначается прописной буквой соответст­вующей обозначению оси и имеет индекс силы. Например, проекция си­лы 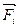на ось х обозначается буквой 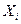, а её проекция на ось y буквой 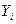(рис.2.8)

Если сила 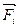образует с положительными направлениями коорди­натных осей х и

y углы, соответственно равные 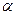и 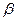= 90° - 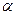то проекции этой силы на указанные оси определятся выражениями:

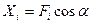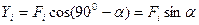; (2.12)

Проекция силы на ось имеет положительный знак в том случае, когда положительное направление силы образует острый угол с поло­жительным направлением оси.

Если же угол между положительным направлением силы и положительным направлением оси больше 90°, то проекция силы на ось имеет отрицательный знак.

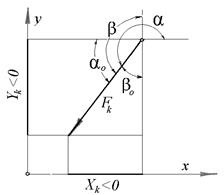
Рис.2.9

На рис.2.9 показана сила 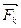, которая образует тупые углы 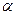и 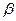с координатными осями х и y.Поэтому её проекции на указанные оси имеют отрицательные знаки:

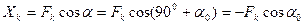(2.13)

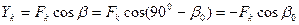(2.14)

Здесь 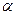₀ и 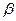₀- острые углы между линией действия силы и коорди­натными осями.

Отсюда вытекает, что проекция силы на любую ось всегда может быть получена умножением модуля силы на косинус остро­го угла между силой и осью. При этом проекция принимается положи­тельной, если положительные направления силы и оси образуют острый угол и отрицательной, если указанные направления образуют тупой угол.