Равнодействующая системы сходящихся сил.

Положим, что в точке А заданного тела действуют силы , , 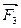… 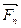, расположенные в одной плоскости (рис.2.4,а), совмещен­ной с плоскостью чертежа. Для нахождения равнодействующей этих сил воспользуемся правилом силового треугольника.

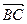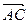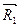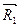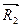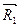Из конца силы (из точки В) отложим вектор , геометрически равный силе и нача­ло силы (точку А) соединим с точкой С. Полученный вектор является равнодействующей сил и , т.е. = + . Аналогично находим равнодействующую сил и 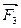, т.е. 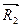= 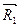+ 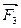= + + 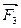, затем равнодействующую 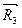= 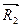+ 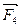= + + + 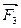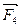и т.д.

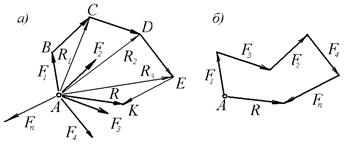
Рис.2.4

В результате последовательного сложения сил, которое называет­ся геометрическим сложением, получаем силовой многоугольник АВСDЕ...К, стороны которого геометрически равны заданным силам. Замыкающий вектор 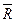, проведенный из начала первой силы в конец вектора ЕК, геометрически равного последней силе, является равнодей­ствующей системы заданных сходящихся сил или их геометрической суммой:

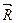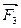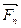= + + +…+ (2.10)

Из приведенного построения легко установить, что для получения равнодействующей системы сил нет необходимости определять промежуточные силы 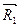, ,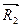... Достаточно вычертить в принятом масштабе силу в конце силы , затем силу 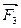в конце и т.д. до последней силы. Замыкающий вектор, проведенный из начала первой силы в конец последней, определяет равнодействующую 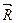заданной системы сил. Направление равнодействующей всегда противоположно общему направлению сторон многоугольника, которые параллельны за­данным силам.

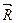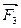Необходимо иметь в виду, что равнодействующая системы схо­дящихся сил не зависит от порядка построения силового многоуголь­ника, т.е. от порядка расположения его сторон. При построении мно­гоугольника не обязательно откладывать силу в конце силы . Можно отложить силу или силу 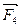в конце силы , затем в любом порядке последовательно вычерчивать остальные силы. На рис.2.4,б показан второй вариант геометрического сложения системы заданных сходящихся сил. Многоугольники сил, пос­троенные на рис.2.4,а и 2.4,б отличаются по форме, но их замыкающие стороны полностью совпадают по величине и направлению.

Итак, равнодействующая плоской системы сходящихся сил равна их геометрической сумме, т.е. определяется замыкающей стороной много­угольника, построенного на заданных силах.

Если к заданной системе сил , , 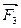… 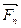присоединить силу 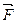, равную по модулю и противоположно направленную их равнодействующей 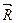(рис.2.5,а), то силовой многоугольник, построенный из некоторой точки О плоскости замкнется в этой точке (рис.2.5,б), т.е. равнодействующая новой системы сил окажется равной нулю.

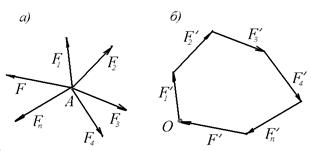
Рис.2.5

Система сил, равнодействующая которых равна нулю, не приводит к изменению первоначального состояния загруженного тела и носит название уравно­вешенной системы сил.

Для равновесия плоской системы сходящихся сил необходимо и достаточно, чтобы многоугольник, построенный на этих силах, был замкнут. Это условие является геометрическим условием равновесия системы сходящихся сил.