Закон классической физики

Известно, что в конце 19 века было объявлено, что законы классической физики успешно работают только в макромире, а в микромире работают другие – квантовые законы. Эта точка зрения была господствующей в течение всего ХХ века. И вот теперь, когда мы на базе законов классической физики выявили модели фотона, электрона, протона, нейтрона и принципы формирования ядер, атомов и молекул, то возникает вопрос: а не ошиблись ли физики прошлых поколений, похоронив возможности классической физики решать задачи микромира? Чтобы ответить на этот вопрос, давайте внимательно проанализируем истоки недоверия к классической физике при поиске приемлемого варианта интерпретации экспериментальной информации об излучении абсолютно черного тела (рис. 119).

Все началось с установления закона излучения абсолютно черного тела (рис. 119). Вывод математической модели этого закона, выполненный Максом Планком в начале ХХ века, базировался на понятиях и представлениях, которые, как считалось, противоречат законам классической физики.

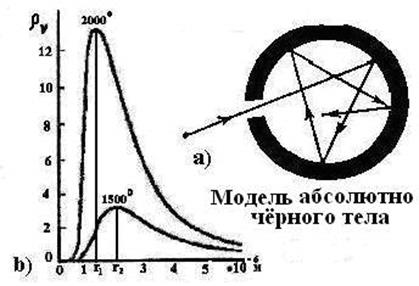
Рис. 119. а) графическая модель абсолютно черного тела;

b) – зависимость плотности излучения абсолютно чёрного тела от длины волны, излучаемых фотонов

Планк ввел в математическую модель закона излучения абсолютно черного тела константу 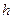с размерностью механического действия, что явно противоречило представлениям о волновой природе электромагнитного излучения. Тем не менее, его математическая модель достаточно точно описывала экспериментальные зависимости этого излучения. Введенная им константа указывала на то, что излучение идет не непрерывно, а порциями. Это противоречило закону излучения Релея - Джинса, который базировался на представлениях о волновой природе электромагнитного излучения, но описывал экспериментальные зависимости лишь в диапазоне низких частот (236), то есть больших длин волн излучения (рис. 119).

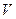Прежде всего, приведем формулу Релея - Джинса, которая удовлетворительно описывает экспериментальную закономерность низкочастотного диапазона излучения (рис. 119). Основываясь на волновых представлениях об электромагнитном излучении, они установили, что энергия , заключенная в объёме абсолютно черного тела, определяется зависимостью

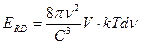, (236)

где 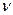- частота излучения; 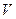- объём полости абсолютно черного тела (рис. 119); 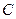- скорость света; 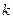- постоянная Больцмана; 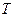- абсолютная температура излучения.

Разделив левую и правую части соотношения (236) на объём 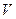, получим объёмную плотность 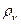электромагнитного излучения

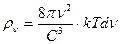. (237)

Вывод этой формулы базируется на представлении о существовании в замкнутой полости абсолютно черного тела (рис. 119, b) целого числа стоячих волн электромагнитного излучения с частотой .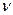

Чтобы получить математическую модель, которая описывала бы весь спектр электромагнитного излучения абсолютно черного тела, Макс Планк постулировал, что излучение идет не непрерывно, а порциями так, что энергия 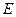каждой излученной порции оказывается равной 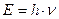, и формула для расчета плотности 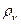электромагнитного излучения абсолютно черного тела оказалась такой (рис. 119)

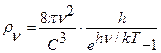. (238)

Величина 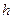- константа с механической размерностью действия. Причем смысл этого действия в то время был совершенно неясен. Тем не менее, математическая модель (238), полученная Планком, достаточно точно описывала экспериментальные закономерности излучения абсолютно черного тела (рис. 119).

Как видно, выражение 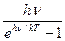в формуле (238) играет роль некоторого существенного дополнения к формуле (237) Релея - Джинса, суть которого сводится к тому, что 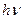- энергия одного излученного фотона.

Поскольку в математической модели закона излучения абсолютно черного тела (238) присутствует математическая модель закона излучения Релея - Джинса (236), то получается, что планковский закон излучения абсолютно черного тела базируется на исключающих друг друга волновых и корпускулярных представлениях о природе излучения.

Несовместимость непрерывного волнового процесса излучения с парциальным процессом явилась веским основанием для признания кризиса классической физики. С этого момента физики начали полагать, что сфера действия законов классической физики ограничена макромиром. В микромире, считают они, работают другие, квантовые законы, поэтому физика, описывающая микромир, должна называться квантовой физикой. Следует отметить, что Макс Планк пытался разобраться со смесью таких физических представлений и вернуть их на классический путь развития, но ему не удалось решить эту задачу.

Спустя почти сто лет нам приходится констатировать, что граница между законами классической и квантовой физики до сих пор не установлена. По-прежнему испытываются значительные трудности при решении многих задач микромира и многие из них считаются не разрешимыми в рамках сложившихся понятий и представлений, поэтому мы вынуждены возвратиться к попытке Макса Планка выполнить вывод математической модели закона излучения абсолютно черного тела на основе классических представлений.

Конечно, чтобы глубже понять физический смысл планковского дополнения надо иметь представление о магнитной структуре фотона, так как в этой структуре скрыт физический смысл самой постоянной Планка 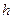. Поскольку произведение 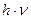описывает энергии фотонов всей шкалы фотонных излучений, то в размерности постоянной Планка и скрыта магнитная структура фотона. Нами уже установлено, что фотон имеет такую вращающуюся магнитную структуру, центр масс которой описывает длину волны 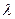, равную его радиусу . В результате математическое выражение константы Планка принимает вид

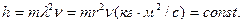(239)

Как видно, константа Планка имеет явную механическую размерность момента импульса. Хорошо известно, что постоянством момента импульса управляет закон сохранения момента импульса и сразу становится ясной причина постоянства постоянной Планка.

Прежде всего, понятие «закон сохранения момента импульса» является понятием классической физики, а точнее - классической механики. Он гласит, что если сумма моментов внешних сил, действующих на вращающееся тело, равна нулю, то момент импульса, действующий на такое тело остаётся постоянным по величине и направлению.

Конечно, фотон не является твердым телом, которое только вращалось бы без перемещения в пространстве, но он имеет массу 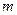и у нас есть все основания полагать, что роль массы у фотона выполняет вращающаяся относительно оси магнитная субстанция, которая вращается и перемещается в пространстве со скоростью света.

Из математической модели (239) постоянной Планка следует, что магнитная модель фотона должна быть такой, чтобы одновременное изменение массы 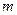, радиуса и частоты 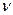вращающихся магнитных полей фотона оставляло бы их произведение, отраженное в математическом выражении постоянной Планка (239), постоянным.

Например, с увеличением массы (энергии) фотона уменьшается длина его волны.Опишем повторно, как это изменение реализуется постоянной Планка (239) в модели фотона (рис. 15 и 16).

Поскольку постоянством константы Планка управляет закон сохранения момента импульса 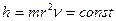, то с увеличением массы 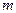фотона растет плотность его магнитных полей (рис. 15 и 16) и за счет этого увеличиваются магнитные силы 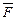, сжимающие фотон, которые все время уравновешиваются центробежными силами инерции, действующими на центры масс этих полей. Это приводит к уменьшению радиуса фотона, который всегда равен длине его волны 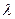. Но поскольку радиус в выражении постоянной Планка возводится в квадрат, то для сохранения постоянства постоянной Планка (239) частота 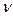колебаний фотона должна при этом увеличиться. В силу этого незначительное изменение массы фотона автоматически изменяет его радиус и частоту так, что момент импульса (постоянная Планка) остается постоянным.

Таким образом, фотоны всех частот, сохраняя свою магнитную структуру, меняют массу, частоту и радиус так, чтобы 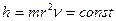. То есть принципом этого изменения управляет закон сохранения момента импульса.

Если задаться вопросом: почему фотоны всех частот движутся в вакууме с одинаковой скоростью? То получается следующий ответ. Потому что изменением массы 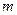фотона и его радиуса управляет закон локализации фотонов 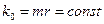таким образом, что при увеличении массы 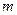фотона его радиус уменьшается и наоборот.

Тогда для сохранения постоянства константы Планка при уменьшении радиуса частота 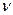должна пропорционально увеличиваться. В результате их произведение 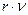остаётся постоянным и равным 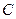. При этом скорость центра масс 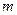фотона (рис. 20, а) изменяется в интервале длины волны таким образом, что её средняя величина остаётся постоянной и равной 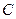и не принимает нулевых значений (рис. 20, а).

Таким образом, постоянством константы 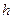Планка управляет один из самых фундаментальных законов классической физики (а точнее - классической механики) - закон сохранения момента импульса. Это - чистый классический механический закон, а не какое - то мистическое кантовое действие, как считалось до сих пор. Поэтому появление постоянной Планка в математической модели закона излучения абсолютно черного тела не даёт никаких оснований утверждать о неспособности классической физики описывать процесс излучения этого тела. Наоборот, самый фундаментальный закон классической физики - закон сохранения момента импульса как раз и участвует в описании этого процесса.

Таким образом, планковский закон излучения абсолютно черного тела является законом классической физики и нет никакой нужды вводить понятие «Квантовая физика». Существует и классический вывод формулы (239) Планка. Он базируется на корпускулярных представлениях о структуре фотонов. Представляем этот вывод.

Так как излучение абсолютно черного тела представляет собой совокупность фотонов, каждый из которых имеет только кинетическую энергию 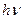, то мы должны ввести в математическую модель закона максвелловского распределения кинетическую энергию 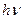фотона и тепловую энергию 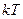совокупности излученных фотонов

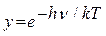. (240)

Далее, мы должны учесть, что фотоны излучаются электронами атомов при их энергетических переходах. Каждый электрон может совершать серию переходов между энергетическими уровнями , излучая при этом фотоны разной энергии. Поэтому полное распределение объёмной плотности энергий излученных фотонов будет состоять из суммы распределений, учитывающих энергии фотонов всех энергетических уровней. С учетом изложенного, закон Максвелла, учитывающий распределения энергий фотонов всех энергетических уровней 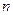атома, запишется так

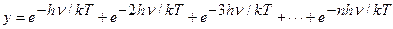, (241)

где 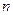- главное квантовое число, определяющее номер энергетического уровня электрона в атоме.

Известно, что сумма ряда (241) равна

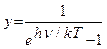. (242 )

Умножая правую часть формулы (242) на константу Планка 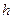и на коэффициент из формулы (236) Релея – Джинса, мы получим результат, описывающий закономерность изменения плотности фотонов в полости чёрного тела (рис. 119, a) от частоты фотонов или их длины волны (рис. 119, b)

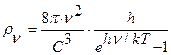. (243)

Это и есть закон излучения абсолютно черного тела (243), полученный Максом Планком в 1901г. Выражение (243) незначительно отличается от выражения (242) коэффициентом, который, как считалось до сих пор, учитывает число степеней свободы электромагнитного излучения абсолютно черного тела. По мнению Э.В. Шпольского его величина зависит от характера волн электромагнитного излучения и может изменяться от до . Однако, в рамках изложенных представлений переменный коэффициент

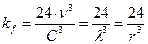(244)

характеризует плотность фотонов в полости абсолютно черного тела. Более точное значение постоянной составляющей 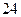этого коэффициента можно определить экспериментально.

Таким образом, мы вывели закон излучения абсолютно черного тела (243), основываясь на чистых классических представлениях и понятиях, и видим полное отсутствие оснований полагать, что этот закон противоречит классической физике. Наоборот, он является следствием законов этой физики. Все составляющие математической модели планковского закона (238) излучения абсолютно черного тела приобрели давно присущий им четкий классический физический смысл.

Обратим особое внимание на то, что в спектре абсолютно чёрного тела присутствуют фотоны (рис. 15, 16 и 119) разных радиусов 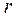, а максимумы температур (2000 и 1500 град. С, рис. 119) формирует совокупность фотонов с определёнными радиусами, величины которых достаточно точно определяет формула Вина

. (245)

Например, максимум температуры 2000 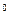С формирует совокупность фотонов с радиусами

. (246)

Это - невидимые фотоны инфракрасного диапазона и у нас сразу возникает возражение. Опыт подсказывает нам, что температуру 2000 С формируют видимые фотоны светового диапазона. Такая точка зрения - яркий пример ошибочности наших интуитивных представлений. Поясним её суть на следующем примере.

Солнечный морозный зимний день с температурой минус 30 град. Цельсия с хрустящим снегом под ногами. Обилие солнечного света формирует у нас иллюзию максимального количества световых фотонов, окружающих нас, и мы готовы уверенно констатировать, что находимся в среде фотонов со средней длиной волны (точнее теперь со средним радиусом) светового фотона 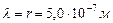(табл. 2). Но закон Вина (245) поправляет нас, доказывая, что мы находимся в среде фотонов, максимальная совокупность которых имеет радиусы (длины волн), равные (табл. 2).

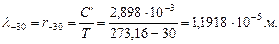(247)

Как видите, наша интуитивная ошибка более двух порядков. В яркий солнечный зимний день при морозе минус 30 градусов мы находимся в среде с максимальным количеством не световых, а инфракрасных фотонов с длинами волн (или радиусами) .

Попутно отметим, что длины волн (радиусы) фотонов изменяются в интервале 16 порядков (рис. 15, 16). Самые большие радиусы ( 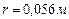) имеют фотоны реликтового диапазона (табл. 2), формирующие минимально возможную температуру вблизи абсолютного нуля, а самые маленькие ( 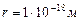) - гамма фотоны (табл. 2) вообще не формируют никакую температуру. Формированием структуры фотонов и их поведением управляют 7 констант.

Представленная информация убеждает нас в справедливости формулы Вина (245) и мы можем найти радиусы фотонов, совокупность которых формирует второй максимум температуры 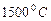(рис. 119, b) в полости чёрного тела (рис. 119, а).

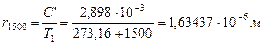. (248)

Как видно (247 и 248), с увеличением температуры радиусы фотонов, совокупность которых формирует температуру, уменьшаются. Это значит, что температуру вблизи абсолютного нуля формируют фотоны, имеющие самые большие радиусы, и мы сейчас убедимся в этом (рис. 120).

Рис. 120: а) фото мизерной части Вселенной; b) зависимость плотности излучения Вселенной от длины волны: теоретическая – тонкая линия; экспериментальная – жирная линия

Считалось, что формула Вина (245) справедлива только для замкнутых систем (рис. 119, а). Однако, мы сейчас увидим, что она идеально описывает не только излучение абсолютно черного тела (рис. 119, а), как замкнутой системы, но и Вселенной – абсолютно незамкнутой системы (рис. 120, а).

Теоретическая зависимость плотности излучения Вселенной (рис. 120, b – тонкая линия) подобна зависимости плотности излучения абсолютно черного тела (рис. 119, а) описываемого формулой Планка (243).

Максимум излучения Вселенной зафиксирован экспериментально при температуре 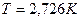(рис. 120, b, точка А) и имеет длину волны . Формула Вина (245) даёт такой же результат

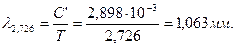(249)

Это яркое доказательство того, что закон Вина справедлив не только для замкнутых систем, таких, как абсолютно чёрное тело (рис. 119, а), но для абсолютно незамкнутых, таких, как Вселенная (рис. 120, a).

Чтобы найти источник максимума излучения Вселенной (рис. 120, b, точки А и 3), обратим внимание на то, что наблюдаемая нами Вселенная состоит из 73 процентов водорода, 24 процентов гелия и 3 процентов более тяжелых элементов. Это значит, что спектр Вселенной (рис. 120, b) формируют фотоны, излучаемые в основном рождающимися атомами водорода. Известно также, что рождение атомов водорода сопровождается процессом сближения электрона с протоном, в результате которого электрон излучает фотоны.

Совпадение теоретической величины длины волны (рис. 120, b, точка 3) с её экспериментальным значением 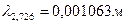(рис. 120, b, точка А), доказывает корректность использования формулы Вина (245) для анализа спектра излучения Вселенной.

Фотоны с длиной волны 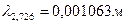обладают энергией

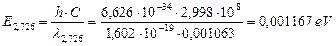(250)

Энергия 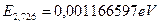соответствует энергии связи электрона с протоном в момент пребывания его на 108 энергетическом уровне. Она равна энергии фотона, излучённого электроном в момент установления контакта с протоном и начала формирования атома водорода.

Процесс сближения электрона с протоном ступенчатый. Он протекает при их совместном переходе из среды с высокой температурой в среду с меньшей температурой или, проще говоря, при удалении от звезд. Сближение электрона с протоном идёт ступенчато. Количество пропускаемых ступеней в этом переходе зависит от градиента температуры среды, в которой движется родившийся атом водорода. Чем больше градиент температуры, тем больше ступеней может пропустить электрон, сближаясь с протоном.

Естественно, что после формирования атомов водорода наступает фаза формирования молекул водорода, которая также должна иметь максимум излучения. Известно, что атомарный водород переходит в молекулярный в интервале температур .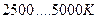

Радиусы фотонов, излучаемых электронами атомов водорода при формировании его молекулы, будут изменяться в интервале:

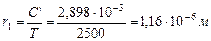; (251)

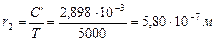, (252)

cоответствующем интервалу длин волн фотонов, форирующих максимум в зоне точки С (рис. 120, b).

Таким образом, у нас есть основания полагать, что максимум излучения Вселенной, соответствующий точке С (рис. 120), формируется фотонами, излучаемыми электронами при синтезе атомов и молекул водорода.

Однако на этом не заканчиваются процессы фазовых переходов водорода. Его молекулы, удаляясь от звезд, проходят зону последовательного понижения температуры, минимальная величина которой равна Т=2,726 К. Из этого следует, что молекулы водорода проходят зону температур, при которой они сжижаются. Она известна и равна 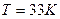. Поэтому есть основания полагать, что должен существовать ещё один максимум излучения Вселенной, соответствующий этой температуре. Длина волны фотонов, формирующих этот максимум, равна

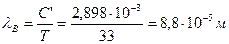. (253)

Этот результат почти полностью совпадает с максимумом в точке 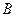на рис. 120 и доказывает, что спектр излучения Вселенной формируется процессами синтеза атомов и молекул водорода, а также - сжижения молекул водорода. Эти процессы идут непрерывно и не имеют никакого отношения к выдуманному Большому взрыву.

Как видно (246 - 253), формула Вина (245) справедлива не только для замкнутых систем, каким является полость абсолютно чёрного тела (рис. 119, а), но и для незамкнутых, подобных Вселенной.