Теорема 1 (Критерий Люка).

В группе U_p , p – простое число, существуют порождающие элементы.

Доказательство:

Действительно, пусть δ₁, δ₂, … , δ_r – все различные показатели, которым по модулю p принадлежат числа 1,2,…,p—1 (то есть порядки этих чисел в U_p). Пусть τ=НОК(δ₁,δ₂,… ,δ_r), и τ= 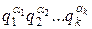- каноническое разложение. Каждый множитель 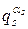этого разложения делит хотя бы одно из чисел δ₁,…,δ_r. Поэтому можем представить одно из таких чисел как δ_j=a 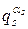. Пусть ξ_j – одно из чисел ряда 1, 2, … , p—1: O_p(ξ_j)=δ_j.

Тогда, согласно Лемме 1, O_p(η)= 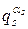, где η= .

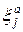Согласно Лемме 2, O_p(g)=τ= 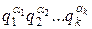, где g=η₁η₂…η_k.

Поэтому, согласно Теореме 3, п.1, τ\(p—1).

Но поскольку числа δ₁, δ₂, … , δ_r делят τ, то любое из чисел ряда 1, 2, … , p—1 является решением сравнения x^τ≡1(mod p), согласно Теореме 2, п.1.

Пользуясь Теоремой 1, §4, п.4, получаем p—1≤τ. Но τ как порядок элемента g не может быть больше, чем p—1, поэтому p—1=τ, а значит g – первообразный корень, или порождающий элемент группы U_p .

□

6.3. Первообразные корни по модулям p^α, 2p^α.

Теорема (о существовании первообразного корня по модулю p^α)

Пусть g – первообразный корень по модулю p, тогда существуют такое число t, что u= 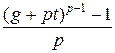не делится на p, и тогда g+pt – первообразный корень по модулю p^α α>1.

Замечание

Число u, заданное условием, является целым в силу теоремы Ферма. Действительно, поскольку g 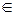U_p, то (g,p)=1 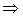(g+pt,p)=1 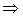по теореме Ферма, (g+pt)^p—1≡1(mod p) 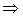p\((g+pt)^p—1 –1).

Доказательство:

Имеем:

g^p—1=1+pT₀

(g+pt)^p—1=1+p(T₀—g^p—2t+pT)=1+pu *

где если t пробегает Z_p, то и u пробегает Z_p (полную систему вычетов по модулю р). Поэтому существует такое t 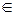Z_p, для которого u не делится на p. При таком t из (*) получаем:

(g+pt)^p(p—1)=(1+pu)^p=1+p²u₂

………………………… **

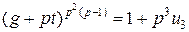
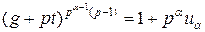
где все u_i, i=2,3,…α—1 не делятся на р.

Пусть 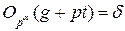. Тогда (g+pt)^δ≡1(mod p^α), откуда g^δ≡1(mod p) 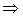(р—1)\δ , и δ\φ(р^α)=р^α—1(р—1) . Тогда δ имеет вид δ=р^r—1(р—1), где 1≤ r ≤ α.

Но (*) и (**) показывают, что сравнение 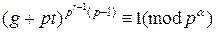верно при r = α и неверно при r < α, то согласно Теореме 3 п.1., δ=р^α—1(р—1) =φ(р^α), и (g+pt) – первообразный корень по модулю р^α.

□

Теорема 2.

Пусть g – первообразный корень по модулю р^α, α≥1. Нечетное g₀ из чисел g, g+р^α будет первообразным корнем по модулю 2р^α .

Доказательство:

Заметим, что g+р^α будет являться первообразным корнем по модулю р^α, а также φ(р^α)=φ(2р^α)=с. Нетрудно проверить, что сравнения g₀^r≡1(mod р^α) и g₀^r≡1(mod 2р^α) могут выполняться лишь одновременно. Первое сравнение выполняется при r=c и не выполняется при r<c (так как g₀ – первообразный корень по модулю р^α), следовательно второе сравнение верно при r=c и неверно при r<c. Значит g₀ – первообразный корень по модулю 2р^α.

□

Доказанные теоремы вкупе с теоремой о существовании первообразных корней по модулю p позволяют сделать следующий

Вывод: Существуют первообразные корни по модулям р^α, 2р^α для всех α. Если известен первообразный корень по модулю р, то, пользуясь Теоремами 1 и 2 настоящего пункта, можно найти первообразный корень по модулям р^α, 2р^α.

Пример.

p=71, наименьший первообразный корень по модулю 71 есть 7.

Найти первообразный корень по модулю 71^α и 2·71^α для всех α.

Согласно Теореме 1, нужно найти такое t, чтобы (g+pt)^p—1—1 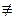0(modp²).

Будем перебирать t:

t=0. g+pt=g=7.

7⁷⁰—1 mod 5041 = (7¹⁰)⁷ –1 mod 5041 = 2814⁷—1 mod 5041 =

= (2814²)³ ·2814—1 mod 5041 = 4226²·4226·2814—1 mod 5041=

= 3854·4226·2814 –1 mod 5041 = 1562 ≠ 0.

Итак, 7 – первообразный корень по модулю 71^α для всех α.

Поскольку 7 – нечетное число, то, согласно Теореме 2, 7 - первообразный корень по модулю 2·71^α для всех α.

Вообще говоря, нам повезло, первое же испытанное число t подошло. В другом случае, возможно, пришлось бы перебирать несколько t, прежде чем отыскали бы первообразный корень.

Разумеется, мы не отыскали все первообразные корни по данному модулю. Алгоритмы нахождения их весьма трудоемки, особенно тогда, когда требуется найти все или несколько первообразных корней.