Криптосистема Гольдвассер-Микали.

Параметры системы: n=pq – число Блюма, z – случайное число из .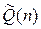

Открытый ключ для шифрования – пара (n,z), секретный ключ для расшифрования – пара (p,q).

Пусть x₁, x₂, … , x_m – последовательность бит открытого текста. Бит шифрованного текста вычисляем по биту открытого текста как 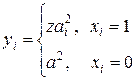, где a_i – случайное число из Z_n.

В итоге шифрования получается последовательность не бит, а чисел, причем y_i является псевдоквадратом по модулю n, если x_i =1, и квадратом, если x_i=0.

Адресату, обладающему секретным ключом, отправляется последовательность чисел шифртекста y₁, y₂, …, y_m , после чего параметр z может быть уничтожен.

Адресат осуществляет расшифрование следующим образом:

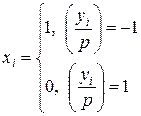, i=1,2,…,m.

Условная стойкость криптосистемы Гольдвассер-Микали основана на предположительной сложности алгоритма распознавания квадратов и псевдоквадратов по модулю Блюма без знания разложения модуля на простые сомножители.

Данная криптосистема имеет существенный недостаток – размер шифртекста значительно превышает размер открытого текста, ведь каждый бит последнего при шифровании преобразуется в число такой же размерности, как n.