Нахождение первообразных корней по простому модулю.
В настоящем пункте будем рассматривать число n, причем n—1= 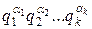 * - каноническое разложение на простые сомножители.
* - каноническое разложение на простые сомножители.
Теорема
On(a)=n—1 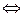 1) an—1≡1(mod n);
1) an—1≡1(mod n);
2) 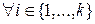 ,
, 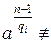 1(mod n).
1(mod n).
Доказательство:
Пусть On(a)=n—1. Тогда (1) выполняется в силу определения порядка элемента в группе. Кроме того, 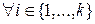 , 1 ≤
, 1 ≤ 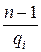 < n—1= On(a), откуда в силу определения порядка элемента, выполняется (2).
< n—1= On(a), откуда в силу определения порядка элемента, выполняется (2).
Пусть теперь выполнены (1) и (2). Покажем, что On(a)=n—1.
В силу (1), On(a)\(n—1). В силу (2), On(a) не делит 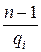
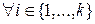 . Значит, On(a)=n—1.
. Значит, On(a)=n—1.
□
Результатами только что доказанной теоремы можно пользоваться для нахождения порождающего элемента группы Up, причем проверять стоит только второй пункт, так как первый для простого модуля выполняется автоматически согласно теореме Ферма. Кроме того, можно вывести правило: если a1, a2 не являются порождающими элементами группы Up, то a1a2 также не является порождающим элементом Up. Отсюда делаем вывод о том, что наименьший порождающий элемент группы Up – простое число.
Пример
p=71. p—1=70=2·5·7.
Для того чтобы a являлся порождающим элементом, необходимо и достаточно, чтобы выполнялись условия: a10 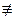 1(mod n), a14
1(mod n), a14 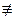 1(mod n), a35
1(mod n), a35 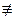 1(mod n).
1(mod n).
Будем испытывать числа из U71. Вместо ab mod 71 для краткости будем писать ab.
2: 210 =30, 214 =54, 235=1. 2 не является порождающим элементом.
3: 310 =48, 314 =54, 335=1. 3 не является порождающим элементом.
5: 510 = 1. 5 не является порождающим элементом.
7: 710 =45, 714 =54, 735=70. 7 – порождающий элемент.
Итак, наименьший порождающий элемент группы U71 (или первообразный корень по модулю 71) есть 7.
Дата добавления: 2018-11-26; просмотров: 1261;











