Система сравнений первой степени. Китайская теорема об остатках.
Рассмотрим систему сравнений
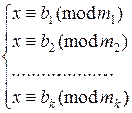 *
*
От системы сравнений вида aix ≡ bi (mod mi) можно перейти к данной способом, указанным в п.1.
Китайская теорема об остатках (I век до н.э. Сунь-Цзе)
Пусть m1,…, mk – попарно простые числа 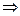 система сравнений (*) имеет единственное решение x0 ≡
система сравнений (*) имеет единственное решение x0 ≡ 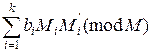 **,
**,
где M= 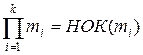 , Mi=
, Mi= 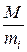 ,
, 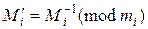 .
.
Доказательство:
Т.к. ms\Mj 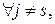
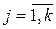
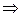
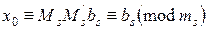
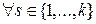
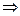 система (*) равносильна системе
система (*) равносильна системе
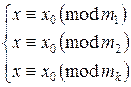 ***
***
т.е. системам (*) и (***) удовлетворяют одни и те же значения x. Системе (***) (в силу свойств 12 и 13 сравнений) удовлетворяют те и только те значения, которые заданы теоремой (т.е. x0).
□
Следствие.
Если в системе ** 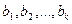 независимо друг от друга пробегают полные системы вычетов по модулям
независимо друг от друга пробегают полные системы вычетов по модулям 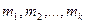 соответственно, то
соответственно, то 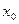 пробегает полную систему вычетов по модулю M.
пробегает полную систему вычетов по модулю M.
Доказательство: в силу свойства 13 сравнений, x0 пробегает ровно M не сравнимых по модулю M значений.
□
Пример
Решить систему сравнений:
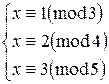
| mi | |||
| Mi | |||
|
Вычислим параметры, необходимые для нахождения решения. Составим таблицу
Согласно китайской теореме об остатках, решением будет являться
x0≡1∙20∙2+2∙15∙3+4∙12∙3(mod 60)≡40+90+144(mod 60)≡34(mod 60).
Ответ: x≡34(mod 60).
Проверка:
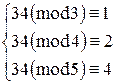
Решение верно.
Дата добавления: 2018-11-26; просмотров: 1180;











