Приведенная система вычетов

Согласно свойству сравнений №15, числа одного и того же класса по модулю m имеют с модулем m один и тот же НОД. Особенно важны классы, для которых он равен 1.

Взяв от каждого из таких классов по одному числу, получим приведенную систему вычетов по модулю m. Обычно ее выделяют из системы наименьших неотрицательных вычетов по модулю m.

Приведенная система наименьших неотрицательных вычетов по модулю m обозначается U_m.

Количество чисел в приведенной системе вычетов по модулю m, очевидно, равно φ(m).

Пример:

Приведенная система вычетов по модулю 15 есть {1; 2; 4; 7; 8; 11; 13; 14}. Заметим, что φ(15)=(5–1)∙(3–1)= 8 и действительно, в приведенной системе вычетов по модулю 15 ровно 8 элементов.

Утверждение 1

Любые φ(m) чисел, попарно несравнимых по модулю m и взаимно простых с m, образуют приведенную систему вычетов.

(Доказательство очевидно как в утверждении 1 пункт 2)

Утверждение 2

Если (a, m) = 1, x пробегает приведенную систему вычетов по модулю m, то ax тоже пробегает приведенную систему вычетов по модулю m . (Доказательство очевидно как в утверждении 2 пункт 2).

Обратный элемент.

Говорят, что элемент b называется обратным к a по модулю m, если a∙b≡1(mod m), и пишут b ≡ a^–1 (mod m).

Вообще, классическая теория чисел не нуждается в таком понятии как обратный элемент, в чем можно убедиться, ознакомившись, например, с [5]. Однако криптология использует системы вычетов как в теоретико-числовом, так и в алгебраическом аспекте, а потому, для удобства изложения алгебраических основ криптологии, мы вводим понятие обратного элемента.

Возникает вопрос – для всех ли элементов по данному модулю m существует обратный (по умножению), и если для каких-то элементов обратный существует, как его найти?

Для ответа на этот вопрос воспользуемся расширенным алгоритмом Евклида. Рассмотрим сначала взаимно простые число a и модуль m. Тогда, очевидно, (a,m)=1. Расширенный алгоритм Евклида позволяет получить числа x и y, такие, что ax+my=(a,m), или, что то же самое, ax+my=1. Из последнего выражения получаем сравнение ax+my≡1(mod m). Поскольку my≡0(mod m), то ax≡1(mod m), а значит полученное с помощью расширенного алгоритма Евклида число x как раз и есть искомый обратный элемент к числу a по модулю m.

Пример.

a=5, m=7. Требуется найти a^-1mod m.

Воспользуемся расширенным алгоритмом Евклида.

7=5∙1+2

5=2∙2+1

2=1∙2

Обратный ход:

1=5–2∙2=5–(7–5∙1)∙2=5∙3–7∙2.

x=3, y=–2.

5^-1≡3(mod 7)

Проверка: 5∙3=15. 15≡1(mod 7).

Действительно, 3 является обратным элементом к 5 по модулю 7.

Итак, конструктивным образом убедились в том, что для чисел, взаимно простых с модулем, существует обратный по этому модулю. А существуют ли обратные элементы для чисел, не являющихся с модулем взаимно простыми?

Пусть (a,m)=d≠1. Тогда a и m представимы в виде a=d∙a₁, m=d∙m₁. Допустим, что для a существует обратный элемент по модулю m, то есть 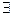b: a∙b≡1(modm). Тогда a∙b= m∙k +1. Или, что то же самое, d∙a₁∙b= d∙m₁∙k +1. Но тогда по теореме 2 из §1 п.1, в силу того, что и левая часть данного уравнения, и первое слагаемое в правой части делятся на d, то d\1, а это не так, поскольку d≠1. Пришли к противоречию, следовательно предположение о существовании обратного элемента неверно.

Итак, мы только что доказали