Непараметрическая идентификация линейных стохастических систем. Уравнение Винера

В приведённых в гл. 2 методах предполагалось, что наблюдаемые выходные переменные полностью определяются наблюдаемыми входными воздействиями. В действительности же в подавляющем большинстве случаев выходные переменные определяются также ненаблюдаемыми и неуправляемыми воздействиями (шумами).

Чтобы получить действительные характеристики объекта, нужно исключить из выходного сигнала составляющие, определяемые шумом, оставив только реакцию на входное воздействие, - отфильтровать выходной сигнал. С другой стороны, в условиях нормальной эксплуатации шумы вызывают отклонение выходных переменных от заданных значений. Стремясь поддержать эти переменные ближе к заданным значениям, автоматические устройства или операторы воздействуют на управляющие органы, то есть на выходные переменные. Следовательно, и в режиме нормальной эксплуатации имеют место изменения входных и выходных воздействий, вследствие чего, проведя статистическую обработку записей этих переменных, можно получить ИПФ или частотную характеристику объекта.

Чтобы получить уравнения связи между статистическими характеристиками входа и выхода для стационарных эргодических случайных сигналов, пользуются их корреляционными функциями или спектральными плоскостями. Выражение взаимной корреляционной функции сигналов x(t), y(t) записывается в виде

. (5.1)

Если в этой формуле участвует одна переменная, т.е. подынтегральное выражение имеет вид 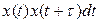, и полученное выражение называется автокорреляционной функцией сигнала.

Структурная схема исследуемого объекта может быть представлена в виде, приведённом на рис. 3.1. Все ненаблюдаемые помехи, воздействующие на различные части объекта, приведены к выходу объекта и представлены в виде аддитивного шума.

Используя уравнение (2.2), можно записать значение выходного сигнала для схемы, приведённой на рис. 3.1, в виде

.

Рис. 3.1. Структурная схема модели Объекта с аддитивным шумом

,

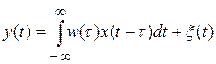ω(τ) – импульсная переходная (весовая) функция (ИПФ) объекта, т.е. сигналы y(t) на выходе объекта, если входной сигнал x(t) представляет собой дельта-функцию δ(t) вида

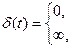
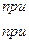
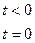
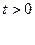
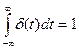
Если входной сигнал x(t)=0 при t<0, то

.

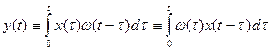Умножив это выражение на 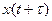, проинтегрировав левую и правую части по 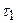в пределах от – T до T и перейдя к пределу при 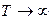, получим выражение

.

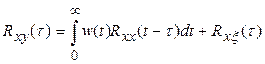Поскольку 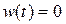при t<0, то, если сигналы 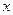и 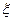не коррелированы, так что 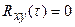, это выражение преобразуется к виду

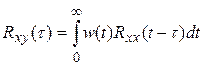(5.2)

Это интегральное уравнение, справедливое для линейных систем, носит название уравнения Винера-Хопфа.

В дискретной форме уравнение (5.2) записывается в виде

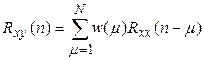(5.2а)

Поскольку при эксперименте получаются только оценки корреляционных функций, значение искомой ИПФ 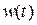так же оказывается приближенным. Структура уравнения такова, что небольшие ошибки в корреляционных функциях приводят к существенным ошибкам при оценке координат ИПФ. Поэтому обычно используют сглаживание решения.

Методы решения уравнения Винера-Хопфа рассмотрены в [4, 11, 18].

Уравнение (5.2) можно решать так же в частотной области. Выполнив преобразование Фурье над уравнением (5.2), получим выражение

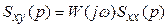(5.3)

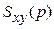где и 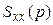- взаимная спектральная плотность сигналов x и y и спектральная плотность сигнала x соответственно (преобразование Фурье от соответствующих корреляционных функций); 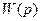- частотная характеристика, 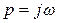. Авто и взаимная спектральная плотности

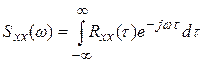
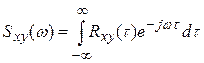
Непосредственное решение этого уравнения (5.3) относительно неизвестной 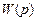может привести к физически нереализуемому результату. Поэтому вначале необходимо провести факторизацию выражений спектральных плоскостей. Физически реализуемое решение находится из выражения

,

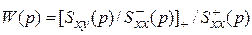где 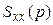представлено в виде 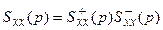, причём 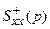содержит все нули и полюсы в левой полуплоскости, а 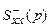- в правой.