Идентификация динамических объектов

Оператор F0 таких объектов имеет память. В этом случае выход Y в момент времени t отражает не только, точнее не столько состоя ние входа X в этот момент, сколько его значения в предыдущие моменты времени. Объект как бы запоминает возмущение X(t) и реагирует на него лишь через определенный промежуток времени. Поэтому динамические объекты часто называют инерционными.

Здесь будем рассматривать идентификацию непрерывной модели линейного детерминированного стационарного объекта. Эта модель для одномерного случая представляет собой обыкновенное дифференциальное уравнение вида

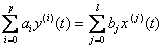(5.107)

где 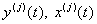- j-я производная функций y и x, т.е. , .

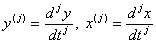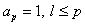Модель определяется p + l + 1 параметрами

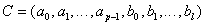. (5.108)

Структурными параметрами модели (5.107) являются числа p и l, которые должны быть выбраны в процессе структурной идентификации. Модель (5.107) часто удобно записать в виде системы дифференциальных уравнений первого порядка (в форме Коши), обозначив y1(t) = y(t):

(5.109)

Естественно обобщить эту модель, приведя ее к виду:

(5.110)

Если модель (5.107) сводится к виду (5.110), то последняя в общем виде не сводится к виду (5.107). Поэтому модель ( 5.110) следует считать наиболее общей формой непрерывной параметрической модели динамического детерминированного линейного стационарного объекта. Эту модель удобно записывать в векторной форме:

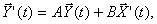(5.111)

где 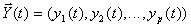- вектор состояния,

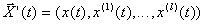- вектор возмущения,

A,B - матрицы коэффициентов модели, причем A = (aqi) - квадратная матрица (p´p), B = (bqj) - прямоугольная матрица (p´(l+1)).

Таким образом, идентифицируемыми параметрами модели (5.111) являются элементы матрицы A и B, т.е. p(p+l+1) параметров модели, которые и образуют две матрицы неизвестных параметров С = (A, B).

Исходной информацией для идентификации в этом случае являются реализации x(t), y(t) в промежутке 0 £ t £ T, характеризующие состояния входа и выхода идентифицируемого объекта

< x(t), y(t) > (0 £ t £ T ). (5.112)

Распространим сказанное на многомерный случай, когда число входов n>1, а число выходов m=1, т.е. вектор входа имеет вид:

.

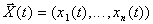В силу линейности вектор состояния 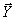образуется как сумма векторов:

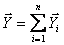(5.113)

где вектор

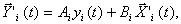(5.114)

отражает влияние i-го входа.

Здесь 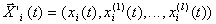- вектор возмущения i-го входа; Ai, Bi - матрицы влияния i-го входа.

Теперь, подставляя (5.113) и (5.114) в (5.111), можно записать уравнение для линейной динамической модели со многими входами

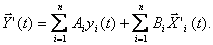(5.115)

Эта модель имеет np(p+l+1) идентифицируемых параметров. При этом информация о работе объекта, необходимая для идентификации, имеет вид:

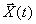< , y(t) > (0 £ t £ T ).

Случай n>1 и m>1 сводится к m-кратному повторению предыдущего.

Идентификация параметров модели. Исходной информацией для построения процедуры идентификации является вид идентифицируемой модели (5.107) и наблюдения (5.112). Необходимо определить p+l+1 параметров

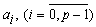и .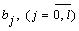

В общем случае, т.е. при произвольных значениях параметров ai и bj, при подстановке реализаций (5.112) в уравнение модели (5.107) равенство в (5.107) выполняться не будет. Естественно подобрать параметры ai и bj такими, чтобы равенство (5.107) было восстановлено или хотя бы правая и левая части выражения (5.107) отличались друг от друга наименьшим образом. Чтобы выполнять это условие, необходимо построить функцию невязки правой и левой частей этого уравнения и минимизировать ее с помощью вариации параметров ai и bj. Сформулируем требования, которым должна удовлетворять эта функция невязки:

1) она не должна принимать отрицательных значений;

2) ее минимум должен соответствовать решению поставленной задачи;

3) этот минимум должен быть равен нулю в случае совпадения структуры модели и объекта.

Этим условиям удовлетворяет невязка в виде среднего квадрата разности правой и левой части уравнения модели (5.107) при подстановке туда функций x(t), y(t) - наблюдений объекта, т.е.

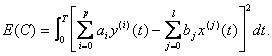(5.116)

Минимизируя это выражение по параметрам ai и bj, которые образуют вектор (2.108), определим искомые параметры. Такая задача минимизации формулируется в виде

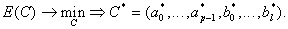(5.117)

Результат минимизации С* и дает значения идентифицируемых параметров, для которых при совпадении структуры объекта и модели E(C*) = 0.

Для решения задачи (5.117) воспользуемся тем, что функция E(C) имеет простую структуру относительно идентифицируемых параметров — это квадратичная форма.

Задача минимизации гладких функций (а квадратичная форма — гладкая функция) сводится к решению системы уравнений, которая образуется в результате приравнивания нулю частных производных:

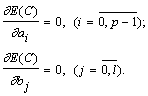
После очевидных преобразований получим следующую систему линейных алгебраических уравнений:

(5.118)

где, напомним, ap = 1 и

(5.119)

где 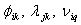- коэффициенты системы уравнений (5.118).

Таким образом, задача идентификации линейной динамической стационарной системы сведена к решению системы линейных алгебраических уравнений, что осуществляется стандартными вычислительными методами.

Однако для вычисления выражений (5.119) необходимо знать производные входного x(t) и выходного y(t) сигналов объекта. Их можно получить двумя способами:

1) численное дифференцирование - связан с локальной (точечной) оценкой производных

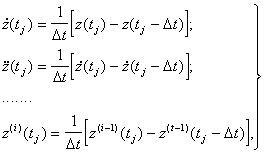(5.120)

где Dt - интервал, характеризующий базу оценок.

Но этот способ обладает двумя недостатками.

Во-первых, точность оценки производных очень быстро падает с ростом порядка производной. Практически удовлетворительно не удается оценить производные выше второго порядка.

Во-вторых, для оценки i-й производной при t= 0 необходимо иметь значения функции при t<0, т.е. z(-Dt), z(-2Dt),...,z(-iDt). Так как этих значений нет в измерениях, то приходится для (5.119) брать пределы интегрирования не [0,T], а [iDt,T], где i - наибольший порядок производной подынтегральной функции.

2) в ряде случаев целесообразно использовать разложение z(t) в ряд по системе заданных в аналитическом виде функций. Тогда полученную аналитическую зависимость, аппроксимирующую z(t), можно дифференцировать нужное число раз.

Все вышеизложенное относилось к простейшей модели (5.107). Если же объект описывается обобщенной моделью (5.111), то функция невязки будет не одна. Количество их будет равно p по числу уравнений (5.110). Для k-ой невязки получаем из k-го уравнения модели (5.110):

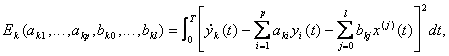(5.121)

где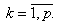

Дифференцируя эти невязки по коэффициентам a и b и приравнивая производные нулю, получаем систему линейных уравнений, откуда определяются идентифицируемые параметры объекта:

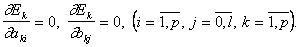(5.122)

Теперь рассмотрим условия применимости рассмотренного метода идентификации. Как было показано, он сводится к решению системы линейных алгебраических уравнений (5.118) или аналогичной ей системы, получающейся из (5.122). Однозначность решения задачи идентификации требует однозначности решения системы (5.118). А это выполняется только в случае, если ее определить

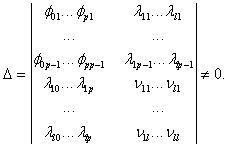(5.123)

Это и есть условие однозначности решения задачи идентификации. Если оно не выполняется, то следует либо взять другую реализацию входа и выхода объекта <x(t), y(t)>, либо уменьшить количество идентифицируемых параметров, т.е. уменьшить числа p и l, тем самым понизить порядок модели.

Обе из указанных мер могут привести к выполнению условия (5.123). Если же, несмотря на предпринятые меры, это условие по-прежнему не выполняется, то следует снова обратиться к одной из них и т.д. до тех пор, пока не выполнится условие (5.123). При этом следует помнить, что если первая мера (новая реализация) не всегда приводит к цели, то вторая (понижение порядка модели) при последовательном применении всегда приводит к выполнению условия (5.123).

Аналогично формулируется условие однозначности для обобщенной модели. Здесь определитель системы (5.122) будет более высокого порядка.