Выбор существенных переменных модели объекта
Для определения структуры модели сложного объекта прежде всего необходимо выяснить, какие входы объекта будут включены в его модель. Для этого прежде всего выявляют всех возможных входов и из них выделяют наиболее существенные. Существенным является тот вход, который наибольшим образом оказывает влияние на выход объекта.
Для этого следует проранжировать выбираемые входы (факторы). В этом случае выбор наиболее существенных факторов очевиден - они должны быть расположены в начале ранжированного ряда.
Поэтому первым этапом задачи идентификации объекта следует считать задачу ранжирования его входов. Так как модели объекта еще нет, то ранжирование можно сделать, например, методом экспертных оценок.
Метод экспертных оценок. Для этого прежде всего определяются все входы объекта. При их выборе принимают во внимание следующее. Входы должны непосредственно воздействовать на объект , не зависеть от других переменных, измеряться и управляться. Исходя из этих соображений составляется ряд входов. Широкому кругу специалистов предлагается расположить эти факторы в порядке убывания степени их влияния на выбранную выходную величину объекта, т.е. проранжировать факторы.
При обработке результатов экспертного опроса весьма эффективным является метод ранговой корреляции. Сущность этого метода заключается в следующем.
Пусть m экспертов ранжируют n факторов. Каждому фактору каждый эксперт присваивает ранг - целое число от 1 до n, приписывая ранг 1 наиболее важному фактору, ранг 2 - следующему по важности и т.д. На основании этих данных составляется матрица рангов
 , (6.1)
, (6.1)
где 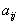 - ранг i-го фактора (
- ранг i-го фактора ( 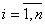 ), определенного j-м экспертом (
), определенного j-м экспертом ( 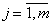 ), номера строк соответствуют номерам экспертов, а номера столбцов - номерам ранжируемых факторов. Это означает, что j-я строка представляет собой мнение j-го эксперта, а i-й столбец - мнение всех экспертов по поводу i-го фактора.
), номера строк соответствуют номерам экспертов, а номера столбцов - номерам ранжируемых факторов. Это означает, что j-я строка представляет собой мнение j-го эксперта, а i-й столбец - мнение всех экспертов по поводу i-го фактора.
При назначении рангов экспертами нужно соблюдать следующие условия:
1. Сумма рангов, назначенных всем факторам, должны быть одинакова для каждого эксперта и равна:
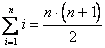 .
.
Это означает, что сумма элементов любой строки матрицы (6.1) должна быть равна:
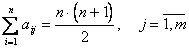 .
.
2. Если эксперт какие-то q факторов считает одинаковыми, то приписывает им один ранг. Этот ранг равен среднему из q целых рангов, которые получены при условии, что эксперту удалось их проранжировать. Например, равноценность двух факторов 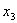 ,
, 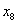 (q=2), стоящих на шестом месте в ранжированном ряду, приводит к тому, что их ранги равны: (6+7)/2=6.5. Как видно, в этом случае ранги могут быть дробными. Отметим, что дробные ранги кратны 1/2.
(q=2), стоящих на шестом месте в ранжированном ряду, приводит к тому, что их ранги равны: (6+7)/2=6.5. Как видно, в этом случае ранги могут быть дробными. Отметим, что дробные ранги кратны 1/2.
На базе данных матрицы (6.1) вычисляем:
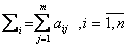 ; (6.2)
; (6.2)
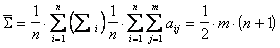 ; (6.3)
; (6.3)
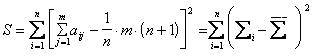 , (6.4)
, (6.4)
где 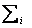 - сумма рангов i-го фактора
- сумма рангов i-го фактора 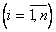 ;
;
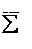 - среднее значение всех рангов;
- среднее значение всех рангов;
S - сумма квадратов отклонений частных рангов от среднего.
Очевидно, максимальное значение S принимает тогда, когда эксперты одинаково проранжируют все факторы и отклонение суммарных рангов от среднего значения будет m(1-n)/2, m(3-n)/2, ... . Сумма квадратов членов этого ряда определяется выражением
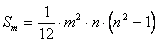 . (6.5)
. (6.5)
Степень согласованности мнений экспертов характеризует коэффициент конкордации (согласованности) W
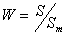 . (6.6)
. (6.6)
Коэффициент конкордации меняется от нуля (отсутствие какого-либо согласия в мнениях экспертов) до единицы (полное согласие). Статистическую значимость коэффициента W определяют в зависимости от числа факторов. При 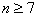 используют
используют 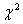 - критерий Пирсона:
- критерий Пирсона:
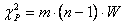 . (6.7)
. (6.7)
Расчетные значение 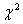 сравнивают с табличным при выбранном уровне значимости
сравнивают с табличным при выбранном уровне значимости 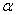 и числе степеней свободы
и числе степеней свободы 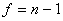 . Гипотеза о наличии согласия между специалистами принимается в том случае если
. Гипотеза о наличии согласия между специалистами принимается в том случае если 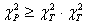 определяется из таблицы распределения Пирсона.
определяется из таблицы распределения Пирсона.
В случае 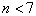 пользуются F-критерием Фишера, расчетное значение которого определяют по формуле:
пользуются F-критерием Фишера, расчетное значение которого определяют по формуле:
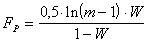 . (6.8)
. (6.8)
с числом степеней свободы 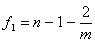 и
и 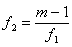 .
.
Мнение специалистов считается согласованным, если расчетное значение критерия Фишера больше или равно табличному 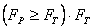 находится из таблицы распределения Фишера.
находится из таблицы распределения Фишера.
Далее оценивают степень влияния каждого фактора на выбранную выходную величину. Для этого используют ряд показателей, но наиболее часто - сумму рангов данного фактора. Чем меньше эта величина, тем сильнее влияет фактор на выходную величину.
Расположим теперь входы в порядке возрастания суммы их рангов: 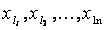 , где индекс
, где индекс 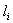 равен номеру фактора с соответствующей суммой рангов (
равен номеру фактора с соответствующей суммой рангов ( 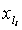 -фактор с минимальной суммой рангов). Здесь на первом месте стоит самый существенный вход (его номер
-фактор с минимальной суммой рангов). Здесь на первом месте стоит самый существенный вход (его номер 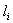 ), а далее следуют остальные в порядке уменьшения их влияния на выход.
), а далее следуют остальные в порядке уменьшения их влияния на выход.
Для анализа результатов ранжирования используют диаграмму рангов (рис. 3.1). Наиболее благоприятным видом диаграммы является возрастание рангов по параболе. В этом случае легко разделить факторы на группы и по К-критерию Линка-Уэллеса отсеять несущественные.

Рис. 3.1
Расчетная величина К-критерия определяется по формуле
 , (6.9)
, (6.9)
где 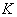 - число факторов, включаемых в группу;
- число факторов, включаемых в группу;
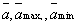 - среднее значение суммы рангов фактора (средние ранги), максимальное и минимальное значения
- среднее значение суммы рангов фактора (средние ранги), максимальное и минимальное значения 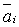 в группе;
в группе;
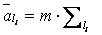
Если значение 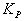 меньше табличного (табл. 3.1) при выбранном уровне значимости
меньше табличного (табл. 3.1) при выбранном уровне значимости 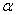 , числе сравниваемых средних К и числа специалистов m, то сравниваем средние ранги
, числе сравниваемых средних К и числа специалистов m, то сравниваем средние ранги 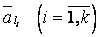 не различаются между собой.
не различаются между собой.
Можно рекомендовать следующий порядок анализа результатов ранжирования. Ориентируясь на вид диаграммы рангов факторы разбивают на отдельные группы. Вычисляют 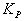 для первой (наиболее значимой) группы факторов. С помощью К-критерия проверяют, различаются ли между собой средние ранги факторов, включенных в эту группу, т.е. образуют ли они в действительности единую группу. Если это подтверждается, тогда объединяют факторы первой и второй (соседней) групп и с помощью К-критерия проверяют эти две группы как единую. Если эти две группы не образуют единую группу, то в первую группу включают не все факторы второй группы, а только один (или несколько) соседний с первой группой фактор и т.д.
для первой (наиболее значимой) группы факторов. С помощью К-критерия проверяют, различаются ли между собой средние ранги факторов, включенных в эту группу, т.е. образуют ли они в действительности единую группу. Если это подтверждается, тогда объединяют факторы первой и второй (соседней) групп и с помощью К-критерия проверяют эти две группы как единую. Если эти две группы не образуют единую группу, то в первую группу включают не все факторы второй группы, а только один (или несколько) соседний с первой группой фактор и т.д.
Факторы, образующие единую группу включаются в программу исследований. Остальные факторы могут быть отброшены, как не оказывающие существенного влияния на выходную величину объекта.
Метод ранжирования факторов удобно применять при разработке модели объекта, которого еще не существует, т.е. на стадии создания. Если же имеются предварительные экспериментальные данные, полученные на объекте, то отсеивающий эксперимент можно выполнить методом корреляционного анализа.
Корреляционный анализ. Этот метод используют для установления статистической связи между переменными объекта. Суть его заключается в определении коэффициентов парной корреляции 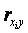 между каждым входом
между каждым входом 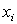 и выходом y объекта по имеющимся экспериментальным данным.
и выходом y объекта по имеющимся экспериментальным данным.
Коэффициент парной корреляции является мерой тесноты линейной статистической связи между двумя случайными величинами. В общем случае его величина изменяется от 0 до 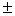 1. Если
1. Если 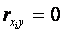 , то связь между
, то связь между 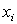 и y отсутствует или она нелинейна. Если
и y отсутствует или она нелинейна. Если  , то связь является линейной, функциональной. При нелинейной зависимости между случайными величинами для анализа меры тесноты их связи используют индекс корреляции.
, то связь является линейной, функциональной. При нелинейной зависимости между случайными величинами для анализа меры тесноты их связи используют индекс корреляции.
В процессе отсеивающего эксперимента из рассмотрения исключаются факторы, у которых с выбранной выходной величиной объекта коэффициент корреляции близок к нулю.
Коэффициент парной корреляции между входом 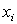 и выходом y объекта определяется по формуле
и выходом y объекта определяется по формуле
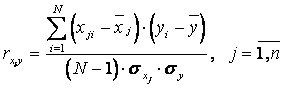 , (6.10)
, (6.10)
где N - число измерений, i - номер опыта, 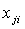 - значение j-го входа в i-м опыте;
- значение j-го входа в i-м опыте;
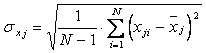 ;
; 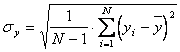 ;
;
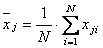 ;
; 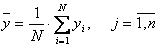 .
.
При наличии высокой корреляции у двух входов 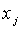 и
и 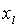
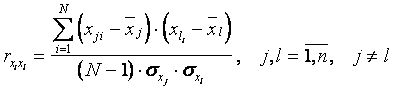 , (6.11)
, (6.11)
любой из них также можно исключить из рассмотрения, так как они однозначно влияют на выходную величину объекта. Исключается, как правило, тот фактор, который труднее определить экспериментально.
После расчета коэффициентов парной корреляции необходимо установить их статистическую значимость, т.е. проверить гипотезу об отличии вычисленного значения коэффициента от нуля. Для этого из табл. 3.2 при выбранном уровне значимости 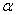 и числе степеней свободы f=N-2 находят критическое значение коэффициента корреляции
и числе степеней свободы f=N-2 находят критическое значение коэффициента корреляции 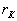 . Линейная связь считается статически значимой, если
. Линейная связь считается статически значимой, если 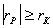 .
.
Таблица 3.1.
Критические значения К-критерия при 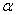 =0,05
=0,05
| Число экспер-тов | Число факторов в группе К | ||||||||||||||||
| m | |||||||||||||||||
| 3.43 | 2.35 | 1.74 | 1.39 | 1.15 | 0.39 | 0.87 | 0.77 | 0.70 | 0.63 | 0.58 | |||||||
| 1.90 | 1.44 | 1.14 | 0.94 | 0.80 | 0.70 | 0.62 | 0.56 | 0.51 | 0.47 | 0.43 | |||||||
| 1.62 | 1.25 | 1.01 | 0.84 | 0.72 | 0.63 | 0.57 | 0.51 | 0.47 | 0.43 | 0.40 | |||||||
| 1.53 | 1.19 | 0.96 | 0.81 | 0.70 | 0.61 | 0.55 | 0.50 | 0.45 | 0.42 | 0.39 | |||||||
| 1.50 | 1.17 | 0.95 | 0.80 | 0.69 | 0.61 | 0.55 | 0.49 | 0.45 | 0.42 | 0.39 | |||||||
| 1.49 | 1.17 | 0.95 | 0.80 | 0.69 | 0.61 | 0.55 | 0.50 | 0.45 | 0.42 | 0.39 | |||||||
| 1.49 | 1.18 | 0.96 | 0.81 | 0.70 | 0.62 | 0.55 | 0.50 | 0.46 | 0.42 | 0.39 | |||||||
| 1.50 | 1.19 | 0.97 | 0.82 | 0.71 | 0.62 | 0.56 | 0.51 | 0.47 | 0.43 | 0.40 | |||||||
| 1.52 | 1.20 | 0.98 | 0.83 | 0.72 | 0.63 | 0.57 | 0.52 | 0.47 | 0.44 | 0.41 | |||||||
| 1.54 | 1.22 | 0.99 | 0.84 | 0.73 | 0.64 | 0.58 | 0.52 | 0.48 | 0.44 | 0.41 | |||||||
| 1.56 | 1.23 | 1.01 | 0.85 | 0.74 | 0.65 | 0.58 | 0.53 | 0.49 | 0.45 | 0.42 | |||||||
| 1.58 | 1.25 | 1.02 | 0.86 | 0.75 | 0.66 | 0.59 | 0.54 | 0.49 | 0.46 | 0.42 | |||||||
| 1.60 | 1.26 | 1.03 | 0.87 | 0.76 | 0.67 | 0.60 | 0.55 | 0.50 | 0.46 | 0.43 | |||||||
| 1.62 | 1.28 | 1.05 | 0.89 | 0.77 | 0.68 | 0.61 | 0.55 | 0.51 | 0.47 | 0.44 | |||||||
| 1.72 | 1.36 | 1.12 | 0.95 | 0.82 | 0.73 | 0.65 | 0.59 | 0.54 | 0.50 | 0.47 | |||||||
| 2.23 | 1.77 | 1.45 | 1.22 | 1.06 | 0.94 | 0.85 | 0.77 | 0.71 | 0.65 | 0.61 | |||||||
Таблица 3.2
Критические значения коэффициента корреляции 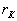 при
при 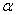 =0.05
=0.05
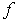
| 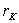
| 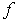
| 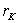
| 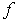
| 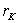
| 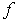
| 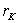
|
| 0.997 | 0.602 | 0.456 | 0.287 | ||||
| 0.950 | 0.576 | 0.444 | 0.273 | ||||
| 0.878 | 0.553 | 0.433 | 0.250 | ||||
| 0.811 | 0.532 | 0.423 | 0.232 | ||||
| 0.754 | 0.514 | 0.381 | 0.217 | ||||
| 0.707 | 0.497 | 0.349 | 0.205 | ||||
| 0.666 | 0.482 | 0.325 | 0.195 | ||||
| 0.632 | 0.468 | 0.304 |
6.2. Оптимальное планирование эксперимента
Главные цели планирования эксперимента заключается в достижении его максимальной точности и минимальной стоимости. Однако достижение максимальной точности требует увеличения числа опытов, что приводит к повышению стоимости эксперимента. Поэтому возникает задача оптимизации в постановке эксперимента.
Методически опыты могут быть поставлены двояко. Традиционный метод постановки опытов состоит в изменении одного какого-либо фактора при сохранении всех других факторов, влияющих на процесс, постоянными. Этот метод постановки опытов известен под названием метода однофакторного эксперимента. При такой методике взаимное влияние факторов учесть невозможно.
Оптимальное планирование эксперимента предполагает одновременное изменение всех факторов, влияющих на процесс, что позволяет сразу установить силу взаимодействия факторов и сократить общее число опытов. Такой метод постановки опытов называется методом многофакторного планирования эксперимента. В результате исследований получают не сечения статических характеристик объекта, как это имеет место в классическом однофакторном методе, а функциональную зависимость выхода объекта от всех факторов 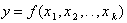 , что очень существенно.
, что очень существенно.
Теория планирования эксперимента и ее приложения в настоящее время развились в самостоятельное научное направление. Попытаемся здесь весьма кратко изложить сущность метода планированного факторного эксперимента применительно к построению модели статики объекта исследования.
|
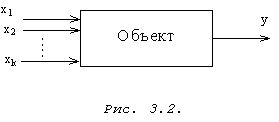
Сущность метода заключается в следующем. Объект исследования рассматривается как “черный ящик” (рис. 3.2). Его входы называют факторами, а выходы — откликами. Целью исследования является построение модели статики объекта, то есть функцию отклика
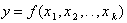 . (6.12)
. (6.12)
Координатное пространство с координатами 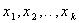 называют факторным пространством, а геометрическое изображение функции отклика в факторном пространстве — поверхностью отклика.
называют факторным пространством, а геометрическое изображение функции отклика в факторном пространстве — поверхностью отклика.
В процессе эксперимента каждый фактор может принимать одно из нескольких фиксированных значений. Эти значения называются уровнями. Сочетание определенных уровней всех факторов определяет одно из возможных состояний объекта. Множество возможных сочетаний уровней факторов определяет множество состояний данного объекта и, следовательно, число возможных различных опытов, равное
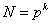 , (6.13)
, (6.13)
где 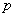 — число уровней факторов;
— число уровней факторов;
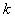 — число факторов.
— число факторов.
Для уменьшения размерности факторного пространства и упрощения модели объекта уменьшают число факторов путем отсеивания малосущественных.
Факторы должны быть управляемыми, независимыми и совместимыми. Это означает, что факторы не должны быть функциями других факторов, должна существовать возможность установления фактора на выбранных уровнях независимо от уровня других факторов, а все комбинации уровней факторов должны давать осуществимые и безопасные для объекта режимы.
Перед началом эксперимента необходимо выбрать его план, то есть определить какие сочетания уровней факторов следует реализовать и в каком порядке. Это очень важный этап в рассматриваемом методе, поскольку этим по сути ограничивается класс регрессионных моделей, среди которых отыскивается модель объекта. Следовательно, требуется задать общий вид отыскиваемой модели: линейная, нелинейная с эффектами взаимодействия, квадратичная и т.п.
Математическая модель чаще всего представляется в виде полинома — отрезка ряда Тейлора, в который разлагается неизвестная функция (6.12):
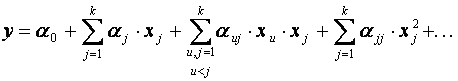 , (6.14)
, (6.14)
где 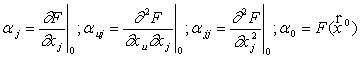 ;
;
индекс 0 означает, что производные вычисляются в точке  .
.
Поскольку в реальном объекте всегда существуют неуправляемые и неконтролируемые переменные, изменение величины 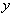 носит случайный характер. Поэтому при обработке экспериментальных данных получаются так называемые выборочные коэффициенты регрессии
носит случайный характер. Поэтому при обработке экспериментальных данных получаются так называемые выборочные коэффициенты регрессии 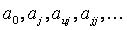 , являющиеся оценками теоретических коэффициентов
, являющиеся оценками теоретических коэффициентов 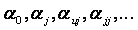 . Уравнение регрессии, полученное на основании опыта, запишется следующим образом:
. Уравнение регрессии, полученное на основании опыта, запишется следующим образом:
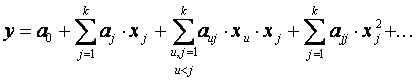 (6.15)
(6.15)
Коэффициент 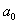 называют свободным членом уравнения регрессии, коэффициенты
называют свободным членом уравнения регрессии, коэффициенты 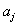 — линейными эффектами,
— линейными эффектами, 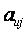 — эффектами парного взаимодействия,
— эффектами парного взаимодействия, 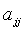 — квадратичными эффектами.
— квадратичными эффектами.
Дата добавления: 2016-06-22; просмотров: 2285;











