Нормирование переменных модели

В процессе эксперимента осуществляются различные комбинации уровней факторов. Эти факторы, как правило, имеют различную физическую природу и размерность. Для упрощения записи и обработки результатов уровни факторов нормируются.

Середине области определения выходной переменной объекта соответствует некоторая комбинация уровней факторов. Эти уровни факторов принимаются как основные (исходные, нулевые, начальные).

Построение плана эксперимента сводится к выбору интервала варьирования факторами 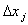, то есть к выбору экспериментальных точек, симметричных относительно основного уровня.

Чаще всего эксперименты проводятся только на двух уровнях факторов. Такие эксперименты называются экспериментами типа 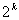. При таком эксперименте уровни факторов представляют собой границы исследуемой области по данному фактору 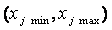. Тогда для любого фактора имеем

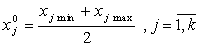; (6.16)

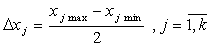. (6.17)

Точка с координатами 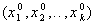называется центром плана (основным уровнем); 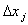— интервал варьирования по оси 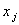. Величина 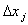своя для каждого фактора. Прибавление 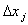к основному уровню дает верхний, а вычитание — нижний уровень фактора.

От системы координат 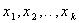перейдем к новой безразмерной системе координат 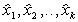путем следующего линейного преобразования координат

, (6.18)

где 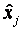— нормированное значение j- го фактора;

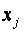— натуральное значение j- го фактора ;

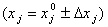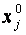— натуральное значение основного уровня.

В нормированном виде для всех факторов верхний уровень равен +1, нижний уровень равен 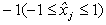, координаты центра плана равны нулю и совпадают с началом координат.

Нормирование переменных существенно упрощает планирование эксперимента, обработку его результатов, построение модели объекта с безразмерными переменными, упрощение модели и проверку ее адекватности. После построения модели с нормированными факторами 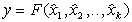и оценки ее адекватности от этой модели переходят к модели с натуральными факторами 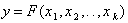, используя нормирующие соотношения (6.18.).

Планирование полного факторного эксперимента

При планировании по схеме полного факторного эксперимента (ПФЭ) реализуются все возможные сочетания уровней факторов. Необходимое количество опытов 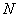при ПФЭ определяется по формуле (6.13).

Если эксперименты проводятся только на двух уровнях факторов и при этом в процессе эксперимента осуществляется все возможные комбинации из 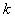факторов, то постановка опытов по такому плану называется ПФЭ типа .

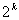ПФЭ типа 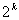широко используется благодаря таким их положительным особенностям, как симметричность относительно центра эксперимента, независимость численных значений коэффициентов уравнения регрессии, полученного экспериментально, от изменения порядка регрессионного полинома, принятого для описания объекта (ортогональность), одинаковая точность модели на равных расстояниях от центра в различных направлениях (ротатабельность). ПФЭ обычно используется при небольших числах факторов .

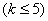С помощью ПФЭ типа 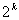может быть получено адекватная модель объекта только в том случае, если в нее не входят степени факторов, то есть этот эксперимент позволяет определить оценки коэффициентов уравнения регрессии только при линейных членах и взаимодействиях:

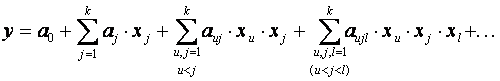(6.19)

Взаимодействие факторов имеет место тогда, когда эффект одного фактора зависит от уровня, на котором находится другой фактор, то есть статическая характеристика объекта нелинейна.

Условия эксперимента описывают с помощью специальной таблицы — матрицы планирования, в которой каждая строка соответствует условиям одного опыта. Для проведения опытов исходные данные по всем факторам желательно свести в таблицу (табл. 3.3). Рассмотрим план ПФЭ 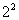. Число опытов .

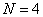Матрица плана ПФЭ типа 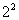приведена в табл. 3.4, в которой введен столбец фиктивной переменной 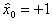для вычисления свободного члена 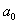. Для сокращения записи обычно опускают единицы в матрице планирования. В первом опыте оба фактора находятся на верхнем уровне, во втором фактор 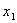— на нижнем, а фактор 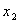— на верхнем и т.д.

Таблица 3.3					Таблица 3.4
Исходные данные					Матрица плана ПФЭ 22
Значения факторов	X1	X2	.....	Xk		Номер опыта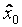
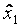
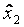
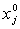
							+1	+1	+1
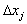
							+1	-1	+1
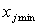
							+1	+1	-1
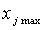
							+1	-1	-1

В случае 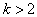при построении матрицы плана ПФЭ типа 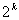руководствуются следующим. При любом числе факторов 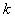необходимо дважды повторить матрицу планирования для случая 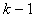сначала при значении 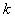-го фактора на верхнем уровне, а затем на нижнем. В табл. 3.5 показано последовательное достраивание матрицы ПФЭ при увеличении 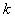от 2 до 4. Для простоты записи плана единицы опущены, а оставлены только знаки.

Таблица 3.5

Матрица плана ПФЭ 22, 23, 24

		План		№ опыта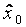
					+	+	+	+	+
					+	—	+	+	+
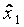
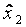
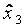
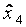
		22			+	+	—	+	+
					+	—	—	+	+
	23				+	+	+	—	+
					+	—	+	—	+
					+	+	—	—	+
					+	—	—	—	+
24					+	+	+	+	—
					+	—	+	+	—
					+	+	—	+	—
					+	—	—	+	—
					+	+	+	—	—
					+	—	+	—	—
					+	+	—	—	—
					+	—	—	—	—

Матрица плана ПФЭ типа 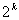обладает следующими свойствами:

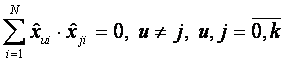; (6.20)

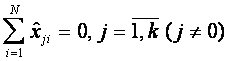; (6.21)

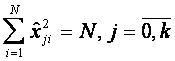, (6.22)

где 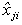— нормированное значение j-го фактора в i-ом опыте.

Свойство (3.20) называется свойством ортогональности матрицы планирования. Это свойство резко уменьшает трудности, связанные с расчетом коэффициентов модели.