Особенности фиксации и обработки результатов моделирования

При проведении имитационного эксперимента необходимо предусмотреть меры по организации эффективной обработки и представления его результатов. В результате эксперимента с моделью системы на ЭВМ вырабатывается информация о состояниях исследуемой системы. Эта информация является исходным материалом для определения оценок искомых характеристик. К качеству оценок, полученных в результате статистической обработки результатов моделирования, предъявляются следующие требования: оценки должны быть несмещенными, состоятельными и эффективными. Возможность получить при моделировании на ЭВМ большие выборки позволяет количественно оценить характеристики системы с учетом этих требований.

При моделировании сложных систем осуществляется многократная реализация на ЭВМ моделирующего алгоритма для получения статистически устойчивых оценок искомых характеристик. При этом накапливается значительный объем статистической информации, для хранения которой требуется большой объем памяти ЭВМ. С целью экономии памяти ЭВМ необходимо производить фиксацию результатов моделирования и их статистическую обработку непосредственно в процессе моделирования с получением текущих оценок для искомых характеристик, используя рекуррентные алгоритмы обработки. то есть без запоминания промежуточных результатов.

Если при моделировании процесса функционирования конкретной системы учитываются случайные факторы, то и среди результатов моделирования присутствуют случайные величины. В такой ситуации в качестве оценок для искомых характеристик рассчитывают средние значения, дисперсии, корреляционные моменты и другие вероятностные характеристики соответствующих случайных величин. При выборе способа фиксации и обработки результатов моделирования необходимо стремиться к использованию минимального объема памяти ЭВМ.

Для иллюстрации рациональной организации вычислительных процессов при моделировании систем на ЭВМ рассмотрим простейшие случаи определения оценок искомых характеристик систем.

Пусть в качестве искомой величины фигурирует вероятность некоторого события A. Предположим, что в результате воспроизведения N реализаций процесса имело место m случаев наступления события A. Тогда в качестве оценки 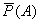для искомой вероятности 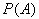можно использовать относительную частоту наступления события A

.

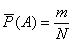Для оценки вероятности достаточно накапливать в памяти ЭВМ лишь числа m и N при обработке результатов моделирования.

Аналогично при обработке результатов моделирования можно подойти к оценке вероятностей возможных значений случайной величины, то есть закона распределения. Область возможных значений случайной величины z разбивается на n интервалов. Накапливается количество попаданий случайной величины в эти интервалы. Оценка для вероятности попадания случайной величины в интервал с номером k служит величина

.

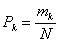Таким образом, для оценки 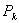достаточно фиксировать n значений 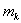, то есть для обработки результатов моделирования требуется n ячеек памяти ЭВМ.

Для оценки среднего значения случайной величины z достаточно накапливать сумму возможных значения случайной величины 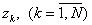, которые она принимает при различных реализациях. Тогда среднее значение

.

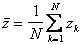В качестве оценки дисперсии случайной величины z при обработке результатов моделирования можно использовать

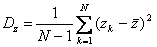. (4.55)

Непосредственное вычисление дисперсии по этой формуле не рационально, так как среднее значение 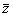изменяется в процессе накопления значений 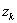. Это приводит к необходимости запоминания всех N значений, что нежелательно. Несложные преобразования (1.55) приводят к более удобной для рациональной организации вычислительного процесса формуле

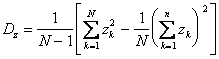. (4.56)

Тогда для вычисления дисперсии достаточно накапливать две суммы: значений 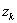и их квадратов .

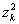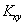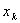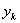
В случае оценки корреляционного момента для случайных величин X и Y с возможными значениями , 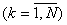используется выражение

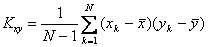. (4.57)

Это выражение можно преобразовать к более удобному виду

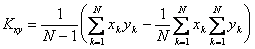, (4.58)

требующему для вычисления 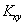накопления трех сумм.

Если при моделировании системы искомыми характеристиками являются математическое ожидание и корреляционная функция случайного процесса 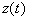, то для нахождения оценок этих величин интервал моделирования 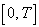разбивают на отрезки с постоянным шагом 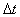и накапливают значения процесса 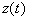для фиксированных моментов времени .

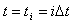При обработке результатов моделирования оценки для математического ожидания и корреляционной функции можно вычислить по формулам:

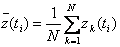; (4.59)

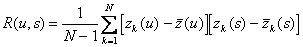. (4.60)

где u и s пробегают все значения.

Для уменьшения затрат машинных ресурсов на хранение промежуточных результатов формулу (1.60) целесообразно преобразовать по аналогии с (1.58) и привести к следующему виду:

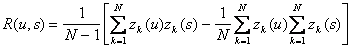. (4.61)

Следует отметить особенности фиксации и обработки результатов моделирования, связанные с оценкой характеристик стационарных случайных процессов, обладающих эргодическим свойством. Пусть рассматривается процесс, для которого верны упомянутые предположения. Тогда поступают в соответствии с правилом: “среднее по времени равно среднему по множеству”. Это означает, что для оценки искомых характеристик выбирается одна достаточно продолжительная реализация процесса, для которой целесообразно фиксировать результаты моделирования. Как известно, в рассматриваемом случае математическое ожидание и корреляционная функция процесса выражаются формулами:

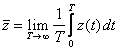; (4.62)

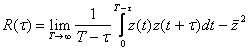. (4.63)

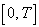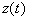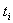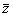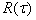На практике при моделировании на ЭВМ системы интервал оказывается ограниченным и, кроме того, значения удается определить только для конечного набора моментов времени . Поэтому для получения оценок и можно использовать приближенные формулы:

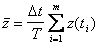; (4.63)

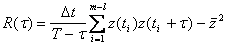, (4.64)

где ; ; , .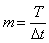

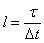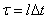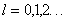Исходя из соотношений (4.63) и (4.64) можно установить целесообразный порядок фиксации и накапливания результатов моделирования.

Мы затронули только простейшие случаи эффективной организации вычислительного процесса для оценок искомых характеристик при моделировании на ЭВМ. Особенности фиксации и статистической обработки результатов моделирования систем на ЭВМ более подробно изложены в источниках [ ] и [ ].