Этапы и принципы моделирования объектов и систем на ЭВМ

Моделирование с использованием ЭВМ (имитационное моделирование) является эффективным средством исследования сложных объектов и систем.

Разработка имитационной модели реальных объектов на ЭВМ и ее исследование осуществляется поэтапно в определенной последовательности. Традиционно такой процесс включает следующие этапы:

1) определение цели и постановка задачи исследования;

2) формализация объекта (системы) с целью построения его математической модели;

3) построение математической модели объекта;

4) разработка и составление моделирующего алгоритма;

5) построение машинной (имитационной) модели объекта (перевод математической модели объекта и моделирующего алгоритма в моделирующую программу и перенесение ее на машинные носители);

6) планирование имитационных экспериментов;

7) имитационные эксперименты с моделью объекта;

8) обработка и анализ результатов имитационных экспериментов;

9) документирование и практическое использование результатов моделирования.

Структурная схема имитационного моделирования изображена на рис. 4.13. В этой схеме этапы построения модели и проведения имитационных экспериментов разделены. Это обусловлено тем, что машинная модель при планировании и проведении эксперимента рассматривается как черный ящик.

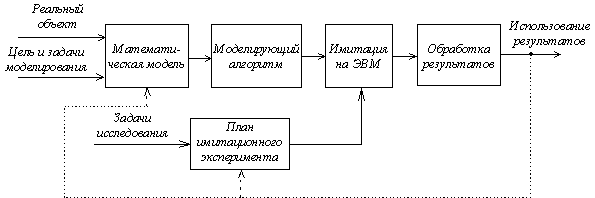
Рис. 4.13

Результаты имитационных экспериментов могут влиять на вид модели объекта и, следовательно, на структуру моделирующего алгоритма. Например, если в процессе эксперимента выяснится, что выходные результаты слабо зависят от того или иного параметра, то это может послужить причиной упрощения модели (исключение данного параметра и соответствующее уменьшение размерности модели) и изменения моделирующего алгоритма.

В зависимости от степени формализации исследуемой системы различают:

- моделирование с применением численных методов;

- вероятностное (статистическое) моделирование с использованием специальных алгоритмических языков программирования.

Моделирование с применением численных методов осуществляют в тех случаях, когда систему удается описать достаточно строгими математическими соотношениями. Его недостаток заключается в том, что структура моделирующего алгоритма и структура информации определяются численным методом, а не структурой и свойствами исследуемого процесса. Изменение требований к режиму моделирования, корректировка модели объекта, повышение требований к точности результатов могут привести к замене численного метода, а следовательно, к замене алгоритма.

Применение метода статистического моделирования делает моделирующий алгоритм по структуре близким к алгоритму функционирования реального объекта. Изменение условий моделирования не приводит к существенным изменениям алгоритма, который может просто дополняться новыми блоками или проигрываться большее число раз на ЭВМ.

Традиционная схема статистического моделирования включает три блока: блок имитации случайных процессов, действующих на систему; блок программы функционирования системы; блок статистической обработки результатов моделирования.

Статистические имитационные модели являются программным воспроизведением структуры реальной системы и тех элементарных действий, которые выполняют ее отдельные элементы. Недостаток статистического метода — необходимость большого количества машинного времени для его реализации.

Моделирующий алгоритм. Для моделирования процесса на ЭВМ необходимо преобразовать его математическую модель в специальный моделирующий алгоритм. Он представляет собой последовательность некоторых операций, выполняемых ЭВМ.

Запись алгоритма для моделирования сложного процесса сразу в виде программы, как правило, представляет значительные трудности. Кроме того, эта запись оказывается весьма неудобной. В самом деле, нагромождение всевозможных деталей, связанных с организацией вычислительной процедуры, делает ее мало обозримой и затрудняет ориентировку в структуре моделирующего алгоритма. Заметим, что построение моделирующего алгоритма является таким этапом исследования процесса, когда уже решены все принципиальные вопросы создания математического аппарата для исследования. Программирование задачи и решение ее на машине относятся скорее к технической части работы. Поэтому желательно сделать запись алгоритма независимой от типа ЭВМ и языка программирования.

Как правило, моделирующие алгоритмы представляются в графической форме или в виде операторной схемы. Графической формой представления моделирующих алгоритмов являются структурные схемы.

Вся совокупность операторов, составляющих моделирующий алгоритм, может быть разделена на три группы: основные, вспомогательные и служебные операторы. Основные и вспомогательные операторы составляют главную часть моделирующего алгоритма.

Основные операторы реализуют соотношения математической модели, описывающие процессы функционирования реальных элементов системы. В отличие от них вспомогательные операторы не предназначены для имитации реального процесса. Они производят вычисление тех параметров и характеристик, которые необходимы для работы основных операторов.

Служебные операторы не связаны с соотношениями математической модели, а обеспечивают взаимодействие основных и вспомогательных операторов при моделировании процесса в автоматическом режиме, синхронизацию работы моделирующего алгоритма, фиксацию результатов и их обработку.

Каждый из рассмотренных операторов должен иметь достаточно ясный, наглядный физический смысл, связанный с природой моделируемого объекта. При этом он должен быть представим последовательностью операций.

Операторы обозначают заглавными буквами с индексами, указывающими номер оператора. Применяется сквозная нумерация операторов, входящих в алгоритм.

Для изображения операторных схем алгоритмов удобно пользоваться операторами следующих типов:

1. Вычислительные операторы ( 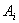). Они описывают сколь угодно сложную вычислительную процедуру и должны удовлетворять следующим требованиям:

— управление от операторов после выполнения предусмотренных им операций должно передаваться только одному оператору независимо от результатов;

— все исходные данные. получаемые от других операторов алгоритма, к моменту начала их работы должны быть известны.

2. Операторы формирования реализаций случайных процессов ( 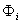). Они предназначены для имитации различных случайных факторов ( случайных событий, величин, векторов, функций ), сопровождающих исследуемый процесс. Исходным материалом для формирования реализаций случайных объектов на ЭВМ служат случайные числа, равномерно распределенные в интервале (0,1). Преобразование этих чисел в реализации случайных объектов с заданными свойствами осуществляет оператор .

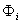3. Операторы формирования неслучайных величин ( 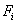). При моделировании сложных систем приходится формировать не только реализации случайных процессов, но и различные константы и неслучайные функции. Сущность операций при этом принципиально не отличается от сущности обычных вычислительных операций, выполняемых оператором 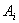. Однако, операторы 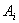, как правило, являются вспомогательными, а 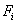— основными. Поэтому выделение операторов 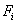в отдельный класс имеет смысл, поскольку они имитируют работу некоторых узлов сложных систем ( чаще всего некоторого вычислительного и управляющего устройства системы ).

4. Счетчики( 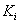). Они относятся к классу служебных операторов по назначению и к арифметическим — по выполняемым функциям. Предназначены для подсчета количества различных объектов, обладающих заданными свойствами ( количества циклов производственного процесса, количества деталей после определенной стадии обработки, количества бракованных изделий и т.д. ). Результаты, выдаваемые счетчиками, часто являются исходными данными для логических служебных операторов, обеспечивающих синхронизацию моделирующего алгоритма. Содержимое счетчиков при моделировании может использоваться для получения вероятностных оценок исследуемых величин.

5. Логические операторы ( 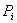). Предназначены для проверки справедливости заданных условий и выработки признаков, обозначающих результат проверки. После реализации логического оператора управление передается одному из двух операторов алгоритма в зависимости от результата проверки.

6. Оператор окончания вычислений (Я). Часто с оператором Я совмещают некоторые другие операции ( выдачу результатов, переход к другому варианту задачи и т.д. ).

При более детальном рассмотрении операторов моделирующего алгоритма могут быть выделены и другие типы операторов, обладающие некоторыми общими функциональными свойствами.

Раскроем смысловое содержание операторов, используя примеры:

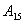— арифметический ( вычислительный ) оператор № 15;

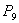— логический оператор № 9;

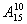— оператор 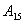после выполнения своей операции передает управление оператору с номером 10;

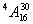— оператор 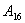получает управление от оператора № 4, выполняет операцию и передает управление оператору № 30;

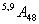— оператору 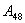управление передается от операторов № 5 и № 9;

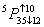— оператор 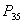передает управление оператору № 10, если условие выполнено, или же оператору № 12, если оно не выполнено, получает управление от оператора № 5.

Если данный оператор получает управление от предшествующего оператора, или передает управление оператору, следующему непосредственно за ним, то верхний индекс опускается, например 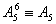; ; 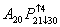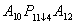. Индекс сохраняется, если последующий оператор получает управление не только от предшествующего ему оператора, но и от другого ( то же и при передаче управления ), например ; ; .

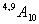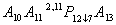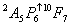В качестве примера построения моделирующего алгоритма рассмотрим простейший вычислительный процесс табулирования функции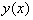

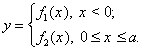(4.54)

Для того, чтобы показать структуру моделирующего алгоритма, соответствующего математической модели (1.54), рассмотрим следующие операторы:

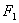— формирование очередного значения независимой переменной 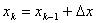( 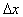— шаг табуляции ), подстановка ;

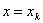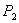— проверка условия ;

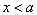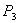— проверка условия ;

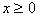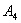— вычисление ;

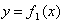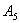— вычисление ;

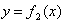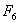— формирование таблицы значений , 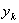и переход к следующему шагу вычислений;

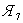— конец вычислений и выдача результатов.

Имея необходимый набор операторов, можно записать операторную схему моделирующего алгоритма в следующем виде:

.

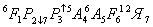На рис. 4.14 представлена структурная схема этого алгоритма, позволяющая получить наглядное представление о его работе.

На различных этапах моделирования составляются укрупненные и детальные структурные схемы моделирования, а также схемы программ.

Укрупненная схема моделирующего алгоритма задает общий порядок действий при моделировании системы без каких-либо уточняющих деталей, показывает, что необходимо выполнить на очередном шаге моделирования. Детальная схема моделирующего алгоритма содержит уточнения, отсутствующие в обобщенной схеме, и показывает не только, что следует выполнить на очередном шаге моделирования системы, но и как это выполнить.

Структурная схема программы отображает порядок программной реализации моделирующего алгоритма с использованием конкретного математического обеспечения. Схема программы представляет собой интерпретацию логической схемы моделирующего алгоритма разработчиком программы на базе конкретного алгоритмического языка и отражает логику машинной реализации модели с использованием конкретных программно-технических средств моделирования. Схема программы также может быть выполнена как в укрупненной, так и в детальной форме.

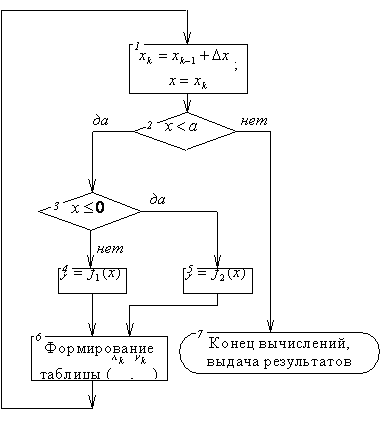
Рис. 4.14

Обычно структурная схема является наиболее удобной формой представления моделирующего алгоритма. В ряде случаев моделирующий алгоритм представляется в форме граф-схемы. В качестве пояснения к граф-схеме алгоритма в тексте дается раскрытие содержания операторов, что позволяет упростить представление алгоритма, но усложняет работу с ним. Для рассмотренного выше примера граф-схема алгоритма имеет вид, представленный на рис. 1.15. Обозначение операторов на граф-схеме соответствует обозначениям для операторной схемы.

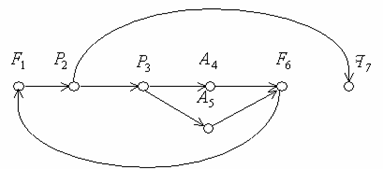
Рис. 4.15.