Идентификация статики линейного детерминированного объекта

Предполагается, что связь между входными и выходными переменными объекта может быть описана линейным уравнением. При этом выходная переменная изменяется только под воздействием наблюдаемых входных сигналов, а какие-либо ненаблюдаемые помехи, вызывающие дополнительное изменение выходной переменной, отсутствуют или их влиянием можно пренебречь. Следовательно, в схеме на рис. 2.1 предполагается, что 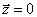, т.е. выходная переменная 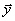наблюдается без помех. Связь между входом и выходом такого объекта описывается функциональной зависимостью

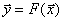
Рассмотрим теперь линейную функцию F и проанализируем специфику ее идентификации.

Модель статики линейного детерминированного объекта с n входами 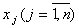и m выходами 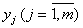имеет единственно возможную структуру и описывается системой линейных алгебраических уравнений:

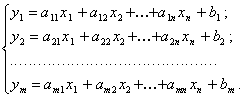(5.7)

где идентифицируются mn коэффициентов 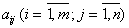и m коэффициентов .

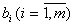Систему уравнений (2.7) можно записать в компактном виде в векторной форме

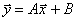, (5.8)

где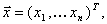

.

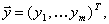
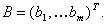
Здесь T - знак транспонирования.

Идентификации в данном случае подлежат вектор B и матрица A.

Модель (2.7) можно рассматривать как совокупность моделей с многомерным входом 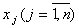и одномерным выходом y (m=1).

Поэтому рассмотрим один выход объекта, то есть случай m=1, n>1.

Модель такого объекта в векторной форме имеет вид:

,

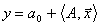где 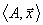- скалярное произведение векторов 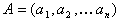и :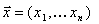

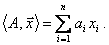
В скалярной форме модель объекта имеет вид

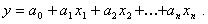(5.9)

Модель имеет n+1 неизвестных параметров 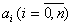, которые подлежат оценке на основе измерений входов и выхода объекта. Эта информация обычно представляется в виде N соответствующих пар значений 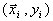, где 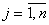, 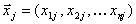- j-е состояние входа объекта, а 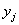- реакция объекта на этот вход.

Обычным подходом к решению этой задачи является приравнивание выходов объекта и модели в N заданных точках 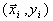, в результате чего получают следующую систему уравнений идентификации:

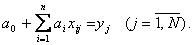(5.10)

Полученные N уравнений с n+1 неизвестными 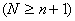имеют однозначное решение, если матрица

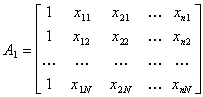(5.11)

невырождена, т.е. 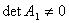и, следовательно, ранг матрицы равен n+1. Это возможно в том случае, если найдется n+1 линейно независимая строка матрицы (2.11).

Поэтому из N строк следует выбрать n+1 линейно независимых строк 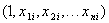, где .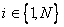

В этом случае из системы (5.10) будут выделены n+1 линейно независимых уравнений

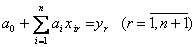, (5.12)

совместное решение которых гарантирует определение точных оценок 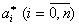идентифицируемых параметров 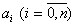объекта, если, разумеется, объект действительно линеен. Покажем это.

Подставим в систему уравнений (5.12) уравнение объекта

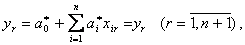
где 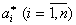- оценки параметров объекта.

Введем невязки

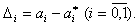
Тогда система уравнений (5.12) запишется в виде

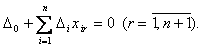(5.13)

Для того чтобы решение системы (5.13) было нулевым, необходимо и достаточно, чтобы определитель этой системы не был равен нулю. Легко заметить, что матрица системы (5.13) такая же, что и матрица системы (5.12), содержит n+1 линейно независимых строк матрицы (5.11) и ее определитель не равен нулю.

В результате имеем:

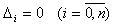
и следовательно, решение системы (5.12) гарантирует точную идентификацию параметров объекта, т.е.

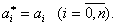
Однако возможно, что объект не строго линеен и существуют незначительные случайные возмущения. При этом может оказаться, что ранг матрицы (5.11) меньше n+1 и из системы (5.10) невозможно выделить n+1 линейно независимых уравнений (5.12) для определения коэффициентов 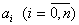объекта. В этом случае возможны следующие подходы к идентификации:

1) повторить измерения входов и выхода объекта в надежде, что первый эксперимент был неудачным, т.е. состояния вектора входа 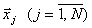были недостаточно разнообразны. Если и на новом экспериментальном материале не выполнится указанное условие, то можно попытаться изменить структуру модели;

2) понизить число идентифицируемых параметров, т.е. исключить рассмотрение одного из входов, например, того, который мало изменяется. Это означает, что число идентифицируемых параметров стало n (а не n+1). Сказанное следует делать до тех пор, пока ранг матрицы (5.11) не совпадет с ее размерностью. При выполнении этого условия из системы (2.10) всегда можно выделить линейно независимые уравнения (2.12) в количестве равном числу 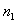оставшихся коэффициентов 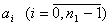. Совместно решая их, находят эти коэффициенты;

3) отказаться от метода интерполяции для определения независимых коэффициентов 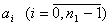, который привел к несовместной системе линейных уравнений. Ввести суммарную невязку выходов модели и объекта.

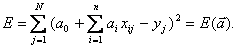(5.14)

Величина Е характеризует степень несоответствия модели и объекта и зависит от параметров 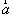модели.

Задачу оценки параметров 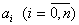можно теперь представить как задачу минимизации невязки (5.14), например, методом наименьших квадратов, т.е. свести к решению системы линейных уравнений:

(2.15)

Система (2.15) имеет следующий развернутый вид:

(5.16)

где суммирование всюду осуществляется по j от 1 до N.

Как видно, эта система линейных алгебраических уравнений относительно искомых параметров 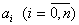. Если ранг матрицы коэффициентов системы (5.16)

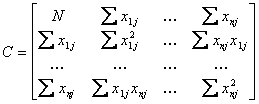(5.17)

равен n+1, то 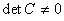и система (2.16) имеет единственное решение 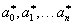, причем оно доставляет минимум функции 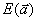(2.14), поскольку .

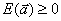В некоторых случаях матрица С системы линейных уравнений может оказаться плохообусловленной, т.е. 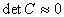. В этом случае малые ошибки измерений 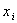и погрешности вычислительных процессов приводят к большим погрешностям в определении коэффициентов 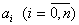модели. Плохая обусловленность матрицы С имеет место в том случае, если некоторые ее строки (или столбцы) почти линейно зависимы. Например, пусть первая и вторая строки матрицы С почти линейно зависимы. Это означает, что

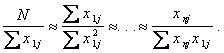
Существует ряд способов определения 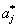из системы линейных уравнений (2.16), в которой 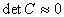. Для этого прежде всего стремятся повысить точность вычислений, подвергают С некоторым эквивалентным преобразованиям, изменяют число опытов N и шаг 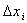дискретности измерения входов 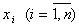.N>n+1.

Идентификация линейных объектов приводит к решению систем линейных уравнений. С этой задачей исследователь часто сталкивается в практике. Это обусловлено, по крайней мере, двумя причинами.

Во-первых, многие задачи линейной оптимизации, идентификации линейных и нелинейных моделей статики, идентификации линейных моделей динамики (дифференциальных уравнений) объекта сводятся к решению систем линейных уравнений.

Во-вторых, большинство нелинейных задач в “малом” линейны, т.е. нелинейные модели в малой окрестности некоторого решения могут быть описаны линейными. Следовательно, первым шагом решения нелинейных задач является исследование линеаризованных моделей, что также связано с решением систем линейных уравнений.

Таким образом, численные методы решения систем линейных уравнений оказываются важным инструментом решения обширного круга научно-технических задач на ЭВМ.