Характеристика проблем и методов моделирования объектов

Под моделированием какого-либо объекта (системы, явления) обычно понимается воспроизведение и исследование другого объекта, подобного оригиналу, в форме, удобной для исследования, и перенос полученных результатов на моделируемый объект. При этом объекты считаются подобными, если характеристики происходящих в них процессов отличаются вполне определенными и постоянными в течение данного процесса коэффициентами. Модель изучаемого объекта при этом может быть иной физической природы, отличной от природы оригинала. Это обстоятельство открывает широкие возможности для применения моделирования в проектировании объектов, обусловленные применением таких эффективных средств, как ЭВМ, динамические стенды, имитаторы, тренажеры.

В основе моделирования лежат информационные процессы, поскольку в процессе реализации модели получают информацию о данном объекте, одновременно в эксперимент с моделью вводится управляющая информация, далее происходит обработка полученных результатов, т.е. информация лежит в основе всего процесса моделирования.

В настоящее время получили применение системы моделирования, отличающиеся высокой степенью автоматизации процесса моделирования, когда наряду с программными средствами управления вычислительным экспериментом используется возможность диалогового общения исследователя с процессом моделирования. Степень автоматизации процесса моделирования тесно связана с управляемостью модели. В этом смысле наличие многих управляемых параметров и переменных модели в реализованной системе моделирования дает возможность поставить широкий эксперимент и получить обширный спектр результатов.

Характеризуя проблему моделирования в целом, необходимо учитывать, что от постановки задачи моделирования до интерпретации полученных результатов существует большая группа сложных научно-технических проблем. К основным из них можно отнести:

- идентификацию реальных объектов;

- выбор вида моделей;

- получение реализаций переменных объекта;

- построение моделей и их реализацию на ЭВМ;

- взаимодействие исследователя с моделью в ходе вычислительного эксперимента;

- проверку правильности полученных в процессе моделирования результатов и выявление основных закономерностей.

В зависимости от объекта моделирования и вида используемой модели эти проблемы могут иметь разную значимость.

В одних случаях наиболее сложной оказывается идентификация, в других — проблема реализации модели на ЭВМ, особенно в случае имитационного моделирования сложных систем.

Для исследования объектов и систем управления используются различные методы моделирования:

- физическое моделирование;

- математическое моделирование на ЭВМ;

- полунатурное моделирование.

Каждый из этих методов имеет свои достоинства и недостатки. Применение того или иного метода определяется в каждом конкретном случае в зависимости от исследуемой системы и условий ее работы. При этом необходимо иметь набор правил и условий, выполнение которых обеспечивает требуемую точность изучения реального объекта по его модели. Эти правила и условия формулируются в теории подобия.

При использовании физического моделирования процессы, протекающие в модели и в оригинале, имеют одинаковую иногда и различную физическую природу. Физическая модель может отличаться от оригинала размерами, скоростью протекания и физической природой процессов или материалами, из которых она изготовлена. Примерами такого моделирования может служить изучение аэродинамических свойств самолета при помощи его макета в аэродинамической трубе, изучение механических колебаний с помощью электрической схемы.

Физическая модель может наиболее полно воспроизводить такие свойства оригинала, которые при теоретическом изучении не могут быть учтены в полной мере. Теоретической базой физического моделирования является теория подобия.

Теория подобия позволяет пересчитать количественные характеристики, полученные при изучении модели, в количественные характеристики оригинала.

При физическом моделировании необходимо для каждого конкретного объекта создать свою модель. Так как изготовление сложных объектов обходится, как правило, очень дорого, требует больших материальных и трудовых затрат, то изменение параметров модели часто нецелесообразно. Поэтому, несмотря на определенные преимущества, физическое моделирование находит ограниченное применение при исследовании сложных объектов и систем управления. Для этой цели широко применяется математическое моделирование.

При математическом моделировании исследование объекта осуществляется посредством модели, сформулированной на языке математики и реализованной, как правило, на ЭВМ с использованием тех или иных математических методов.

При моделировании на ЭВМ в качестве объекта моделирования (оригинала) выступает исходные уравнения, представляющие математическую модель реального объекта, а в качестве модели — процессы, протекающие в соответствии с этими уравнениями и воспроизводимые на ЭВМ в виде “машинных решений” путем реализации программ.

Математическое моделирование объектов и систем управления осуществляется на АВМ и ЦВМ, поэтому часто такие способы называют аналоговым и цифровым моделированием.

В математическом моделировании выделяют имитационное моделирование, под которым понимается воспроизведение объектов с имитацией случайными величинами и случайными процессами элементов оригинала, которые не удается представить определенными математическими моделями. При этом процесс функционирования объекта (системы) представляется в виде определенного алгоритма, который реализуется на ЭВМ.

На некоторых тактах работы имитационной модели используются параметры, выбираемые исследователем, так называемые управляющие воздействия. Выбор управляющих воздействий осуществляется из некоторого множества и обычно имеет критерий качества этого выбора, т.е. функцию, которую следует оптимизировать. Тогда перед тем как вводить управляющие воздействия в имитационную модель, решается оптимизационная задача по их отысканию, и лишь после этого найденные оптимальные значения вводятся в имитационную модель. В этом случае имитация позволяет моделировать отклик системы на оптимальные управления ею. Если множество управляющих воздействий не слишком богато, то все они могут быть перепробованы в имитационной системе. Результаты имитационного моделирования в таком случае позволит провести оценку управляющих воздействий — отбросить заведомо плохие, упорядочить и т.п.

Таким образом, имитационное моделирование рассматривают так же, как управляемый эксперимент, производимый на ЭВМ. В таком эксперименте определенные математическими моделями части объекта моделирования взаимодействуют с имитирующими возмущающие воздействия и некоторые части объекта генераторами случайных величин. Это взаимодействие проводится по определенным в эксперименте правилам, а результаты моделирования подвергаются статистической обработке.

Результаты имитационных экспериментов могут влиять на вид модели после завершения серии прогонов ее на ЭВМ (исключение малозначимых параметров и входов и т.д.).

Полунатурное моделирование — это моделирование с реальной аппаратурой, при котором часть системы моделируется, а остальная часть является реальной.

Применение такого метода моделирования становится необходимым в тех случаях, когда не удается описать работу некоторых элементов системы математически. Например, при исследовании радиолокационных (РЛ) САУ летательных аппаратов в условиях помех процесс приема и передачи антенной отраженного сигнала трудно поддается математическому описанию. Поэтому приходится РЛ и другую аппаратуру, не поддающуюся математическому описанию, воспроизводить в натуре, а остальные звенья САУ — математически на ЭВМ. Естественно работа всей замкнутой схемы моделирования должна проходит в натуральном масштабе времени. Такое моделирование системы управления позволяет анализировать как всю систему в целом, так и отдельные ее элементы, исследовать влияния кинематики и динамики элементов реальной аппаратуры на работу САУ, несмотря на то, что их математическое описание отсутствует.

В процессе полунатурного моделирования удачно сочетаются достоинства математического и натурного моделирования и может быть достигнуто оптимальное взаимодействие между вычислительными и натурными экспериментами. В настоящее время методы полунатурного моделирования эффективно применяют при проектировании разнообразных автоматических управляющих систем.

Необходимость применения таких методов возникает, если:

- объект управления находится еще в стадии проектирования, а элементы устройства управления реально существуют;

- объект не может испытываться в лабораторных условиях;

- элементы устройства управления имеют нелинейные характеристики, трения, помехи, которые при составлении их уравнений не учитывались;

- проведение натурных экспериментов по настройке устройства управления на объекте дорого или вообще недопустимо.

Для проведения полунатурного моделирования необходимо иметь сопрягающие устройства для связи модели (ЭВМ) с внешними реальными элементами.

Структура полунатурного моделирования системы управления представлена на рис. 4.12. Система включает также модель генератора возмущающих воздействий для выполнения имитационных экспериментов и устройство сопряжения с объектом (УСО), т.е. преобразующие элементы для связи модели объекта с реальной аппаратурой. Включение в схему моделирования дополнительных преобразующих элементов искажает результаты моделирования реального процесса. Поэтому основные свойства этих элементов должны быть учтены при обработке результатов моделирования или же при организации самого процесса моделирования. Например, если преобразующие элементы инерционны, то можно хотя бы частично скомпенсировать инерционность введением в модель объекта форсирующих звеньев.

Цель моделирования при проектировании САУ — выбор структуры и параметров отдельных устройств автоматической системы, отвечающих требованию выполняемых ею функций и заданным показателям качества ее работы. При выбранной структуре автоматической системы моделированием определяется лишь оптимальные значения параметров устройства управления, в наибольшей степени влияющих на заданные показатели качества.

Моделирование применяется также для исследования спроектированной автоматической системы с целью выяснения ее надежности, устойчивости, чувствительности и поведения при отказе тех или иных элементов, при различных (в том числе аварийных) возмущающих и задающих воздействиях.

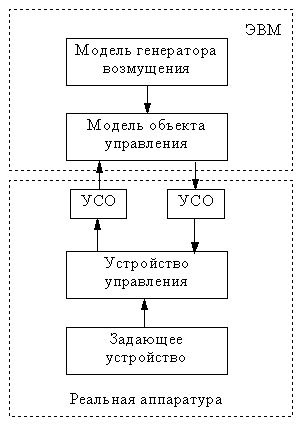
Рис. 4.12

При изучении процессов в реальных системах и их математических моделях различают три типа времени:

1. Реальное, во время которого протекают процессы в реальных условиях и системах;

2. Модельное (системное), во время которого протекают процессы в модели системы. Использование модельного времени позволяет анализировать процессы в моделях в ускоренном или замедленном темпе, а также останавливать решение для изучения процессов в какой-то момент времени;

3. Машинное, во время которого происходит моделирование системы на ЭВМ, оно регистрируется таймером ЭВМ.