Идентификация статики нелинейного детерминированного объекта
Предположим, что помехи 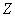 , действующие на выходную переменную объекта, малы или совсем отсутствуют (
, действующие на выходную переменную объекта, малы или совсем отсутствуют ( 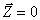 в схеме на рис. 5.1 ), т.е. вход
в схеме на рис. 5.1 ), т.е. вход 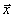 и выход
и выход 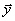 объекта являются детерминированными сигналами (без помех ), наблюдаемыми точно. Тогда выходной сигнал
объекта являются детерминированными сигналами (без помех ), наблюдаемыми точно. Тогда выходной сигнал 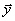 полностью определяется только наблюдаемым входным сигналом. Поведение моделируемого объекта такого рода в общем случае описывается многомерной функцией многих переменных
полностью определяется только наблюдаемым входным сигналом. Поведение моделируемого объекта такого рода в общем случае описывается многомерной функцией многих переменных
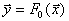 (5.18)
(5.18)
Рассмотрим одномерный случай. Поведение нелинейного одномерного детерминированного объекта описывается нелинейной функцией одной переменной общего вида
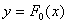 (5.19)
(5.19)
Априорные сведения о виде функции 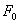 (оператора реального объекта) могут быть различными по объему и содержанию. Трансформация этих сведений в определенную функцию
(оператора реального объекта) могут быть различными по объему и содержанию. Трансформация этих сведений в определенную функцию
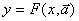 (5.20)
(5.20)
с неизвестными параметрами 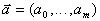 составляет предмет структурной идентификации. Основные подходы к выбору структуры модели (2.20) опирается на кусочно-линейное и функциональное представление зависимости выхода объекта от его входа, причем частным случаем последнего является разложение в ряд по заданной системе функций.
составляет предмет структурной идентификации. Основные подходы к выбору структуры модели (2.20) опирается на кусочно-линейное и функциональное представление зависимости выхода объекта от его входа, причем частным случаем последнего является разложение в ряд по заданной системе функций.
Относительно функции 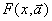 возможна различная степень информированности.
возможна различная степень информированности.
1. Вид функции 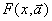 известен, тогда задача поиска математической модели сводится к определению неизвестных параметров
известен, тогда задача поиска математической модели сводится к определению неизвестных параметров 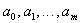 (параметрическая идентификация ).
(параметрическая идентификация ).
2. Функция 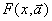 выбирается из совокупности функций
выбирается из совокупности функций 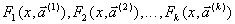 , в которых размерность векторов
, в которых размерность векторов 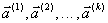 различная. Требуется определить, какая из перечисленных функций является искомой (структурная идентификация) и, соответственно, найти неизвестные параметры
различная. Требуется определить, какая из перечисленных функций является искомой (структурная идентификация) и, соответственно, найти неизвестные параметры  (параметрическая идентификация).
(параметрическая идентификация).
Рассмотрим общую для этих случаев задачу параметрической идентификации функциональной модели, когда функция задана в аналитической форме и непрерывно дифференцируема (отметим, что кусочно-линейная модель является частным случаем функциональной).
В этом случае задача идентификации сводится к определению параметров 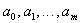 на основе экспериментальных наблюдений, т.е. апостериорной информации. Для этого достаточно потребовать, чтобы в каждом из зафиксированных состояний модель соответствовала объекту. Наиболее распространенным методом решения такой задачи является интерполирование и приближение.
на основе экспериментальных наблюдений, т.е. апостериорной информации. Для этого достаточно потребовать, чтобы в каждом из зафиксированных состояний модель соответствовала объекту. Наиболее распространенным методом решения такой задачи является интерполирование и приближение.
При интерполировании предполагают, что выходы объекта и модели являются близкими, если они совпадают на заданной системе значений входа 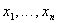 , т.е.
, т.е.
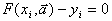 ;
; 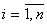 , (5.21)
, (5.21)
где 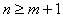 .
.
Выражение (5.21) в общем случае является системой нелинейных уравнений относительно неизвестных параметров. Наличие шумов и погрешностей измерения, как правило, делает систему уравнений (5.21) несовместной и затрудняет ее решение. Поэтому наиболее употребительным является метод приближения.
Для приближения характерна минимизация некоторого функционала, характеризующего различие 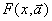 и
и 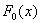 во всем промежутке . В практических приложениях чаще всего используется дискретное квадратичное приближение (метод наименьших квадратов), при котором задача идентификации представляется в виде минимизации функционала
во всем промежутке . В практических приложениях чаще всего используется дискретное квадратичное приближение (метод наименьших квадратов), при котором задача идентификации представляется в виде минимизации функционала
, 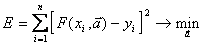 (5.22)
(5.22)
равного сумме квадратов отклонений выходов объекта и модели на заданной системе точек 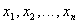 .
.
Очевидно, что величина 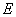 характеризует степень несоответствия модели и объекта и зависит от параметров модели
характеризует степень несоответствия модели и объекта и зависит от параметров модели 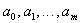 . Эти коэффициенты надо подобрать так, чтобы величина
. Эти коэффициенты надо подобрать так, чтобы величина 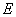 была наименьшей. Минимум
была наименьшей. Минимум 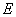 при правильном выборе структуры модели
при правильном выборе структуры модели 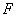 равен нулю, т.е. модель может быть адекватной объекту. Если же структура модели отличается от структуры объекта, то минимум
равен нулю, т.е. модель может быть адекватной объекту. Если же структура модели отличается от структуры объекта, то минимум 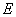 не будет равен нулю, тем не менее задача синтеза модели по-прежнему сводится к задаче минимизации функции невязки
не будет равен нулю, тем не менее задача синтеза модели по-прежнему сводится к задаче минимизации функции невязки 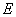 .
.
Необходимым условием минимума 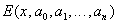 является выполнение равенств
является выполнение равенств
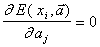 ,
, 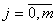 , (5.23)
, (5.23)
или
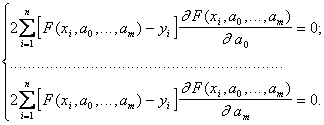 (5.24)
(5.24)
После преобразования
 (5.25)
(5.25)
Система уравнений (5.25) содержит столько же уравнений, сколько неизвестных коэффициентов 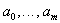 , и называется системой нормальных уравнений.
, и называется системой нормальных уравнений.
Величина 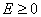 при любых
при любых 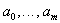 , следовательно, у нее обязательно должен существовать хотя бы один минимум. Поэтому, если система нормальных уравнений (5.25) имеет единственное решение, то оно и является минимумом для величины
, следовательно, у нее обязательно должен существовать хотя бы один минимум. Поэтому, если система нормальных уравнений (5.25) имеет единственное решение, то оно и является минимумом для величины 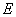 .
.
Система уравнений (5.25) в общем случае является системой трансцендентных уравнений относительно искомых параметров  . Поэтому для решения такой системы часто обращаются к поисковым методам минимизации.
. Поэтому для решения такой системы часто обращаются к поисковым методам минимизации.
Применение поисковых методов для минимизации функции невязки (5.25) открывает большие возможности перед идентификацией. Однако поиска можно избежать, если идентифицируемая модель линейна относительно искомых параметров  .
.
Модели такого рода являются частным случаем функциональных моделей и образуются в результате разложения искомой функции по заданной системе функций.
Рассмотрим вкратце такой случай. Пусть модель 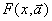 линейна относительно неизвестных параметров и имеет вид
линейна относительно неизвестных параметров и имеет вид
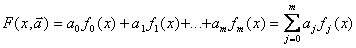 , (5.26)
, (5.26)
где 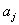 — искомые коэффициенты модели,
— искомые коэффициенты модели, 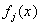 — известные непрерывно-дифференцируемые функции входной переменной.
— известные непрерывно-дифференцируемые функции входной переменной.
Система функций 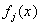 должна быть линейно независимой, т.е. никакая линейная комбинация ее элементов не может быть равна нулю при любых
должна быть линейно независимой, т.е. никакая линейная комбинация ее элементов не может быть равна нулю при любых 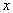 .
.
В результате эксперимента можно получить 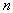 наблюдений
наблюдений
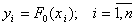 . (5.27)
. (5.27)
Для определения неизвестных коэффициентов  воспользуемся методом наименьших квадратов. В этом случае функция невязки (5.22) после подстановки в нее выражение (5.26) принимает вид
воспользуемся методом наименьших квадратов. В этом случае функция невязки (5.22) после подстановки в нее выражение (5.26) принимает вид
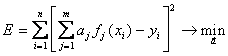 . (5.28)
. (5.28)
Теперь найдем неизвестные параметры 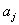 модели из необходимых условий минимума квадратичной функции относительно неизвестных параметров
модели из необходимых условий минимума квадратичной функции относительно неизвестных параметров 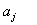 (
( 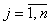 ):
):
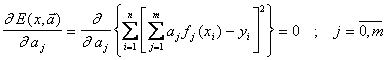 . (5.29)
. (5.29)
Вычислив частные производные и перенеся в правую часть члены, не содержащие коэффициентов 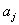 , получим систему линейных нормальных уравнений метода наименьших квадратов:
, получим систему линейных нормальных уравнений метода наименьших квадратов:
 (5.30)
(5.30)
решение которой дает значения идентифицируемых параметров модели.
В векторно-матричной форме система уравнений (5.30) примет вид:
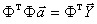 , (5.31)
, (5.31)
где
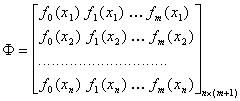 ;
; 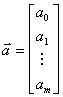 ;
; 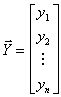 .
.
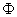 –– прямоугольная матрица размерности
–– прямоугольная матрица размерности 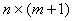 , задающая значения функций
, задающая значения функций 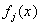 при проведение
при проведение 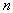 наблюдений;
наблюдений;
 —
— 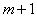 - мерный вектор искомых коэффициентов модели;
- мерный вектор искомых коэффициентов модели;
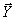 —
— 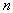 - мерный вектор замеров выхода объекта;
- мерный вектор замеров выхода объекта;
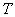 — операция транспонирования матрицы.
— операция транспонирования матрицы.
Информационная матрица Фишера 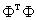 является квадратной, положительно-определенной и невырожденной, когда
является квадратной, положительно-определенной и невырожденной, когда 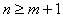 и хотя бы
и хотя бы 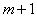 измерений выхода объекта проведен при различных уровнях входной переменной
измерений выхода объекта проведен при различных уровнях входной переменной 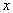 . В этом случае матрица Фишера имеет обратную матрицу
. В этом случае матрица Фишера имеет обратную матрицу 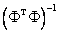 и решением системы (5.31) будет вектор
и решением системы (5.31) будет вектор
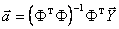 . (5.32)
. (5.32)
Систему уравнений (5.32) можно сразу разрешить, если функции 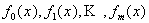 выбрать в виде ортогональных полиномов, обладающих свойством:
выбрать в виде ортогональных полиномов, обладающих свойством:
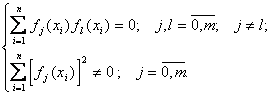 (5.33)
(5.33)
Последнее означает, что хотя бы в одной из точек 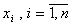 многочлен
многочлен 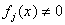 Такие многочлены называют ортогональными многочленами Чебышева.
Такие многочлены называют ортогональными многочленами Чебышева.
При выполнение условий (5.33) в левой части каждого из уравнений системы (5.30) остается только один член ( диагональные элементы ) и эта система распадается на 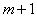 уравнений с одним неизвестным в каждом. Поэтому сразу можно написать выражение для искомых коэффициентов
уравнений с одним неизвестным в каждом. Поэтому сразу можно написать выражение для искомых коэффициентов
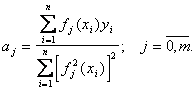 (5.34)
(5.34)
Многочлены Чебышева определяются по формулам:
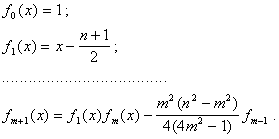 (5.35)
(5.35)
Из формулы (5.35) следует, что полином 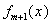 зависит только от объема выборки
зависит только от объема выборки 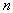 . Следовательно, вычисленные по формуле (5.34) коэффициенты
. Следовательно, вычисленные по формуле (5.34) коэффициенты 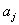 не зависят от того, каков будет порядок модели (5.26). Зная многочлены Чебышева
не зависят от того, каков будет порядок модели (5.26). Зная многочлены Чебышева 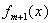 при каждом увеличении степени уравнения статики объекта на единицу используют все ранее найденные коэффициенты
при каждом увеличении степени уравнения статики объекта на единицу используют все ранее найденные коэффициенты 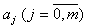 вычисляют только один коэффициент
вычисляют только один коэффициент 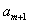 . Эта особенность делает полезным использование ортогональных полиномов Чебышева при решении задач идентификации объекта путем последовательного улучшения модели.
. Эта особенность делает полезным использование ортогональных полиномов Чебышева при решении задач идентификации объекта путем последовательного улучшения модели.
Несмотря на преимущества использования полиномов Чебышева, для практических целей, как правило, ограничиваются степенным разложением функции 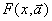 , т.е.
, т.е. 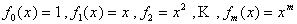 . Такой подход существенно упрощает программирование решения задач на ЭВМ. В этом случае модель имеет вид:
. Такой подход существенно упрощает программирование решения задач на ЭВМ. В этом случае модель имеет вид:
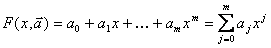 . (5.36)
. (5.36)
Подставляя это выражение в функции невязки (5.28), получим
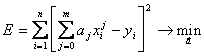 . (5.37)
. (5.37)
Минимизируя эту функцию методом наименьших квадратов, находим следующую систему линейных уравнений:
 (5.38)
(5.38)
где всюду суммирование осуществляется по 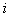 от 1 до
от 1 до 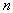 .
.
Решая систему линейных уравнений (5.38), находим искомые коэффициенты модели 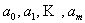 .
.
Если матрица коэффициентов системы (5.38) неособенная, т.е. ее определитель не равен нулю, то найденное решение единственное, причем оно обеспечивает 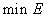 .
.
Трудности в вычислении коэффициентов  из системы нормальных уравнений (5.38) возникает в случае, когда матрица системы плохо обусловлена, тогда приходится привлекать методы регуляризации.
из системы нормальных уравнений (5.38) возникает в случае, когда матрица системы плохо обусловлена, тогда приходится привлекать методы регуляризации.
Адекватность модели можно оценить по степени близости выходов объекта и модели на заданной системе точек.
Схема оценки адекватности модели приведена на рис.5.2.
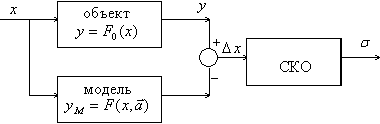
Рис. 5.2
В качестве меры близости выходов используют норму равномерного приближения
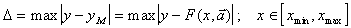 (5.39)
(5.39)
или дискретную норму среднеквадратичного приближения
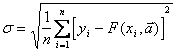 . (5.40)
. (5.40)
Модель считается адекватной, если выполняется условие 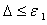 , или
, или 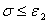 ,
,
где 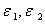 — заданные положительные числа.
— заданные положительные числа.
Уменьшение ошибки модели можно достичь путем увеличения степени полинома (5.36). Однако с некоторого момента при повышении степени полинома (5.36) среднеквадратическая ошибка вместо того, чтобы уменьшаться, может увеличиваться из-за искажения результатов измерения выхода неконтролируемыми помехами.
Поэтому в рассмотренной выше процедуре идентификации нелинейной модели неясным остается вопрос выбора числа 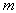 — степени модели (5.36).
— степени модели (5.36).
Обычно его определяют на основе анализа наблюдений выходов объекта и модели.
Если для оценки адекватности выбирается равномерная норма (5.39), то полином, который доставляет
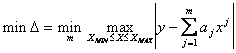 , (5.41)
, (5.41)
является оптимальным.
В случае, когда выбирается среднеквадратичная норма, то полином, который доставляет
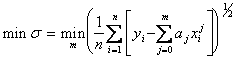 , (5.42)
, (5.42)
является полиномом наилучшего среднеквадратичного дискретного приближения.
Следует отметить, что, если результаты измерений выхода объекта в процессе идентификации содержат помехи, то выбор оптимальной величины 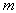 из условия (5.41) и (5.42) приведет к неоправданному увеличению степени полинома (5.36) и усложнению модели. В этом случае желательно выбрать
из условия (5.41) и (5.42) приведет к неоправданному увеличению степени полинома (5.36) и усложнению модели. В этом случае желательно выбрать 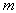 с учетом величины ошибки измерения выхода объекта.
с учетом величины ошибки измерения выхода объекта.
Среднеквадратическую ошибку (СКО) измерения 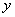 можно определить по результатам повторных измерений
можно определить по результатам повторных измерений 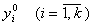 выхода объекта при фиксированном значении
выхода объекта при фиксированном значении 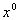 входа
входа
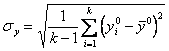 , (5.43)
, (5.43)
где 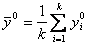 .
.
Среднеквадратическая ошибка модели
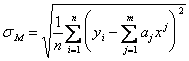 , (5.44)
, (5.44)
при фиксированных значениях 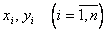 и
и 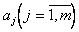 зависит от степени полинома (5.36). Естественно потребовать, чтобы СКО модели была соизмерима с СКО измерения выхода объекта, т.е.
зависит от степени полинома (5.36). Естественно потребовать, чтобы СКО модели была соизмерима с СКО измерения выхода объекта, т.е.
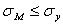 (5.45)
(5.45)
При выборе 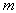 условие (5.45) проверяется в процессе последовательного увеличения степени полинома (5.36), начиная с
условие (5.45) проверяется в процессе последовательного увеличения степени полинома (5.36), начиная с 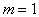 . При этом для каждого
. При этом для каждого 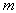 требуется заново вычислять все коэффициенты
требуется заново вычислять все коэффициенты 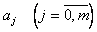 . Если же в качестве базисных функций
. Если же в качестве базисных функций 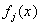 выбрана ортогональная система полиномов Чебышева, то увеличение числа членов рада (5.36) на единицу не требует пересчета найденных ранее коэффициентов. Последовательное увеличение
выбрана ортогональная система полиномов Чебышева, то увеличение числа членов рада (5.36) на единицу не требует пересчета найденных ранее коэффициентов. Последовательное увеличение 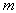 продолжается до тех пор, пока не будет выполнено условие (5.45).
продолжается до тех пор, пока не будет выполнено условие (5.45).
Рассмотрим другой подход к определению наилучшей степени полинома (5.36). Пусть выход объекта 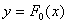 измерена достаточно точно и является гладкой и низкочастотной функцией. Если
измерена достаточно точно и является гладкой и низкочастотной функцией. Если 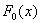 есть полином степени
есть полином степени 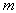 , то
, то
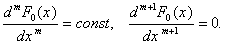
Используем это свойство полинома для оценки числа 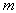 . Производные
. Производные 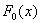 неизвестны, поэтому заменим их конечными разностями выхода объекта
неизвестны, поэтому заменим их конечными разностями выхода объекта 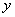 в точках
в точках 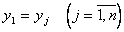 :
:

где 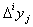 — конечная разность
— конечная разность 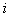 -го порядка в точке
-го порядка в точке 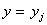 ;
;
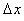 — шаг изменения
— шаг изменения 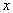 в эксперименте.
в эксперименте.
Обычно значения 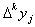 флуктуируют, поэтому следует определить среднее значение их модулей
флуктуируют, поэтому следует определить среднее значение их модулей
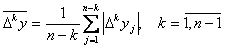 .
.
Если при некотором 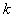 все конечные разности порядка
все конечные разности порядка 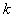 или среднее значение их модулей близко к нулю, то следует принять
или среднее значение их модулей близко к нулю, то следует принять 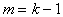 .
.
Дата добавления: 2016-06-22; просмотров: 2479;











