Адекватность модели и объекта

Переход от исследования объекта к исследованию модели и подтверждение пригодности модели для решения задач моделирования требует оценки качества полученной модели, т.е. проверку адекватности модели и объекта. Никогда нельзя говорить об абсолютной адекватности, при которой модель по всем свойствам соответствует объекту, так как в зависимости от цели исследования могут строиться различные модели объекта. Например, при исследовании влияния размещения пассажиров на центровку самолета моделью человека может служить мешок с песком, для конструктора одежды - манекен, а для медико-биологических исследований - животные. Таким образом, всякая модель имеет характер проекции и отражает отдельные свойства объекта. В связи с этим основное подтверждение адекватности модели заключается в том, чтобы убедиться в возможности использования полученной модели для решения той задачи, ради которой эта модель и строилась. Поэтому адекватность предполагает воспроизведение моделью с необходимой полнотой всех свойств объекта, существенных для целей данного исследования.

Количественно степень адекватности модели и объекта можно оценить путем сравнения их выходных сигналов при подаче одинаковых входных воздействий на объект и его модель. Такое сравнение предпочтительно на основе новой информации, отличной от того множества данных, которое использовалось в процессе идентификации объекта.

Структурная схема вычисления оценки ошибки модели статического объекта приведена на рис. 4.8.

Рис. 4.8.

Пусть проведено l опытов при различных уровнях входных воздействий 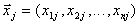из области 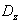их допустимых значений и получены реализации выходов объекта 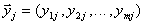и выходы модели , .

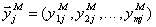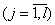Ошибки модели абсолютная 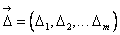и приведенная 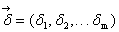для оценки ее адекватности вычисляются по формулам:

Абсолютная – максимальная ошибка по i-му выходу:

, ;

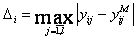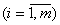Приведенная ошибка по i-му выходу:

, ;

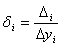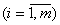СКО в серии l опытов:

, ,

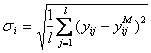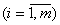где 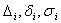- абсолютная, приведенная и среднеквадратичная ошибки модели по i-му выходу 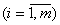; 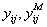- значение i-го выхода объекта и модели в j-ом опыте 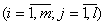; 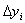- максимальное изменение i-го выхода объекта 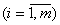при допустимых значениях входов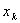 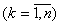из области .

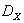Если величины этих ошибок меньше некоторого заданного положительного числа, то модель адекватна объекту.

Теперь рассмотрим оценку модели динамического объекта. Положим, что после идентификации получена модель одномерного объекта в форме линейного дифференциального уравнения вида

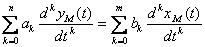, (4.42)

где 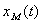- входной сигнал модели;

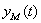- выходной сигнал модели;

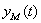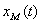n,m - наивысшие порядки производных и соответственно .

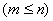Пусть получены реализации входа 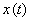и выхода объекта на отрезке времени 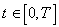, где 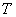- длина реализации (время наблюдения). Теперь качество модели можно оценить путем сравнения 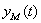и либо непосредственно на графике (визуально), либо введя некоторую формальную меру расстояния между этими сигналами.

Выходные сигналы объекта и модели при одном и том же входном сигнале различаются, так как их дифференциальные уравнения и начальные состояния неидентичны. Для оценки адекватности модели и объекта введем критерий их близости по разности выходных сигналов, т.е. реакций на один и тот же входной сигнал 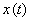, например следующего вида

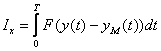, (4.43)

где 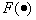- некоторая выпуклая функция.

В частности

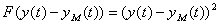. (4.44)

В общем случае оценка адекватности проводится для различных форм входного сигнала 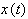. Отсюда следует идея необходимости усреднения по входным сигналам и начальным условиям, т.е. введения операции математического ожидания оценки :

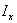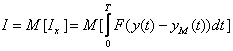. (4.45)

Выражение выходного сигнала имеет довольно сложный вид, что затрудняет аналитическое исследование зависимости I от коэффициентов модели, поэтому вводятся и другие критерии. В частности, если уравнение модели имеет вид

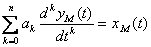, (4.46)

то для оценки близости модели и объекта удобным оказывается функционал от разности входных сигналов 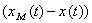модели и объекта, обеспечивающих один и тот же выходной сигнал

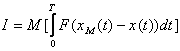, (4.47)

при условии, что 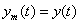. В этом случае выходной сигнал модели и объекта будем обозначать .

Тогда, подставляя (4.46) в (4.47), имеем

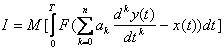, (4.48)

т.е. функционал в явном виде зависит от коэффициентов модели, что удобно для аналитического исследования.

Развивая эту идею, можно формализовать удобный функционал для общего случая модели (1.42)

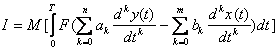. (4.49)

Выражение

, (4.50)

называется обобщенной ошибкой модели. В качестве функции 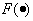, как правило, принимают квадрат обобщенной ошибки

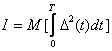. (4.51)

Этот функционал удобен тем, что в явном виде зависит от параметров модели и от доступных измерению входного и выходного сигналов объекта. Однако при вычислении этого функционала возникают определенные трудности, связанные с дифференцированием сигналов 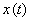и , а также с необходимостью выполнения операции математического ожидания. Структурная схема вычисления обобщенной ошибки и оценки критерия 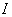представлена на рис. 1.9, где 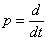- оператор дифференцирования.

Рис. 4.9

Однако по условиям физической реализуемости можно создавать лишь устройства, порядок числителя которых меньше(или равно) порядка знаменателя, т.е. можно реализовать устройства с операторам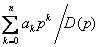и

и ,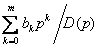

где 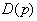- многочлен степени больше или равно ; .

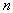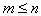Тогда структурная схема вычисления обобщенной ошибки 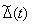и оценки критерия 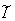будет иметь вид, представленной на рис. 4.10.

Рис. 4.10

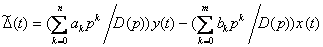; (4.52)

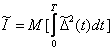. (4.53)

Структурной схеме, изображенной на рис. 4.10, эквивалентна схема, приведенная на рис.4.11.

Рис. 4.11

Таким образом, обобщенная ошибка 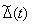, измеряемая с помощью физически реализуемых устройств, отличается от обобщенной ошибки 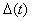тем, что 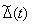является результатом преобразования 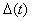фильтром с передаточной функцией 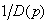. В силу конечности полосы пропускания этого фильтра происходят искажения сигнала обобщенной ошибки. Эти искажения будут тем меньше, чем больше полоса пропускания фильтра.

Если величина ошибок модели и оценок критериев приближения удовлетворяют требованиям к качеству модели, то модель считается адекватной объекту и может быть использована для решения задач моделирования, оптимизации и управления. В противном случае модель необходимо усовершенствовать путем изменения структуры и введения в нее неучтенных ранее факторов.