Постановка задачи и описание проблемы идентификации объектов

Объект идентификации в общем случае представляется в виде многополюсника, изображенного на рис. 5.1, а где 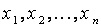— наблюдаемые входы объекта; 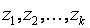— ненаблюдаемые входы объекта; 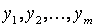— наблюдаемые выходы объекта.

Рис. 5.1

Многомерный объект удобно представлять в векторной форме (рис.2.1,б) где

;

;

.

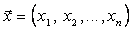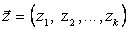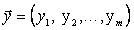В общем случае переменные 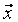, , 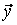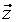являются случайными функциями времени, , , .

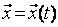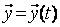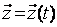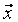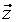Объект связывает входы и с выходом 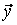некоторым априори неизвестным оператором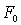

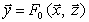. (5.1)

Однако идентифицируется не оператор 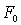, а оператор модели 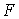, связывающий наблюдаемые входы и выходы:

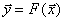(5.2)

Ненаблюдаемый вход 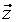рассматривается как случайная помеха, затрудняющая определение оператора .

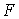Задачей идентификации является построение такого оператора модели 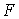, который был бы в определенном смысле близок к оператору объекта 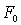, то есть 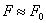. Однако указанная близость весьма относительна, так как операторы 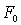и 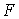могут иметь разную структуру и разное число входов. Поэтому близость операторов непосредственно оценить трудно или просто невозможно, тем более что часто об операторе 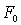мало что известно.

В связи с этим в теории идентификации близость операторов оценивают по их реакциям на одно и то же входное воздействие 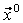, то есть по выходам объекта

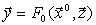
и модели

,

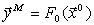где 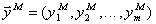— вектор выхода модели.

Степень близости этих реакций в каждый момент времени в общем случае оценивается функцией невязки 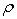. Эта скалярная функция двух векторных аргументов — выходов объекта и модели

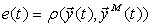, (2.3)

которая обладает следующими свойствами:

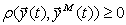для любых , ;

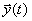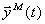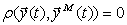при ;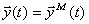

непрерывна и выпукла вниз по обоим аргументам.

Этим требованиям соответствует функция невязки

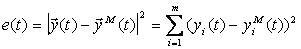, (5.4)

которая чаще всего применяется в задачах идентификации.

Можно ввести единую меру близости выходов объекта и модели на всем интервале наблюдения 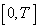, а не только в каждой точке, как (5.3.). Такой мерой в непрерывном случае может быть интеграл

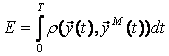(5.5)

Значение 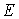явно зависит от :

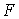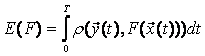(5.6)

и задача идентификации заключается в ее минимизации путем соответствующего выбора оператора модели .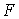

Следовательно, модельный оператор 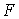должен быть таким, чтобы 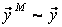, то есть выходы модели и объекта при одинаковых входных воздействиях должны быть эквивалентны.

Определение класса оператора, в котором ищется решение задачи идентификации, практически не поддается формализации и нуждается в эвристических решениях.

Для того чтобы начать процедуру идентификации необходимо иметь априорную информацию о структуре модели объекта и достаточном объеме измерительной (апостериорной) информации для определения параметров модели.

Априорная информация, которой необходимо располагать еще до наблюдения входов и выходов объекта, часто имеет качественный характер. Она должна ответить на вопрос, что представляет собой структура модели идентифицируемого объекта. Структура модели определяется в зависимости от основных свойств объекта.

Определение структуры оператора 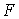модели составляет задачу структурной идентификации. Если же структура этого оператора определена и априори известна, то процесс идентификации сводится к определению параметров этой структуры по имеющейся измерительной информации, то есть к решению задач параметрической идентификации.

При решении задач идентификации широко используются процедуры минимизации функции или функционала и задачи оптимального планирования эксперимента.