Методы упрощения моделей

Когда полученная математическая модель является сложной, т.е. неразрешимой, разработчик прибегает к ее упрощению и использованию более глубокой абстракции. В практических задачах исследования процессов функционирования сложных систем часто желателен обратный процесс — процесс расширения модели. При этом начинают с построения простой модели, а затем усложняют ее. Эволюционный характер процесса конструирования модели упрощает решение поставленной задачи. Сначала решаются более простые задачи с помощью простой модели, а затем ставятся более сложные задачи, что требуют достижения большего соответствия между моделью и реальным объектом, что приводит к усложнению модели.

В обоих случаях возникает необходимость упрощения математических моделей объекта.

Наиболее распространенными являются следующие методы упрощения моделей:

1) расчленение сложной системы на ряд более простых подсистем (декомпозиция);

2) выделение существенных свойств и воздействий и учет остальных в параметрической форме (метод макромоделирования);

3) линеаризация нелинейных процессов в некоторой области изменения переменных;

4) приведение систем с распределенными параметрами к системам c сосредоточенными параметрами (введение более жестких предположений и ограничений);

5) пренебрежение динамическими свойствами процессов.

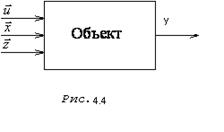
Декомпозиция. В общем случае конечной целью декомпозиции является разбиение пространства переменных объекта (рис.4.4.) {y₁, y₂,..., y_n, u₁, u₂,..., u_r, x₁, x₂,..., x_m, z₁, z₂,..., z_l} нa q подпространств меньших размерностей, в которых учитывается только связь данного выхода y_i с соответствующими переменными. Если любой выход имеет связь с остальными выходами, то декомпозиция практически невозможна. Если общая модель объекта имеет вид неявного выражения достаточно большой размерности

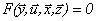(4.33)

и выходы y_i с объекта не имеют связи между собой, то сложную модель (4.33.) можно представить в виде совокупности эквивалентных ей n более простых частных моделей для каждого из выходов

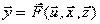, (4.34.)

где .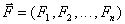

Благодаря проведенной декомпозиции системы значительно облегчается задача ее теоретического исследования.

Макромоделирование. При использовании метода макромоделирования в исходном пространстве переменных оставляются (т.е. учитываются) только те из них, которые влияют на выходные переменные наиболее сильно. Остальные неучтенные воздействия могут быть учтены в параметрической форме путем изменения коэффициентов при учтенных переменных (в случае мультипликативных воздействий ) либо путем введения свободных членов (для аддитивных воздействий).

При построении упрощенных моделей с учетом только существенных факторов широко используется метод адаптивной модели, т.е. модели, коэффициенты которой подстраиваются таким образом, чтобы некоторая мера расхождения (невязка) выходов модели и объекта принимала допустимые (минимальные) значения. Для этого используют критерии минимизации невязок. Те переменные, которые стабилизируются и не приводят к изменению выходных переменных, в модели не отражаются. Структура упрощенной модели, называемой макромоделью, может быть трехканальной с каналом управления u и каналами контролируемых x и неконтролируемых z воздействий, двухканальной и одноканальной (рис. 4.5.)

Рис. 4.5

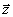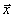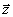Учет возмущений в двухканальных и и в одноканальных моделях производится параметрически за счет подстройки коэффициентов оставшихся каналов.

Полная математическая модель

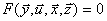. (4.35)

Трехканальная макромодель

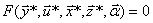. (4.36)

Двухканальная макромодель

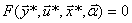. (4.37)

Одноканальная макромодель

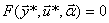, (4.38)

где 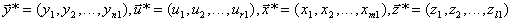- векторы контролируемых переменных, причем выполняются условия n₁<n, m₁<m, r₁<r, l₁<l, свидетельствующие о сокращении числа переменных в макромодели;

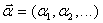- вектор настраиваемых коэффициентов;

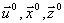- векторы неконтролируемых переменных;

Рассмотрим в качестве примера идею одного из методов адаптации моделей(компенсационный метод).

Рис. 4.6

На рис.4.6: e = (y - y_M) - сигнал рассогласования выходов объекта и модели;

АИ — алгоритм идентификации.

Алгоритм идентификации позволяет настраивать модель объекта по критерию минимума ошибки ε путем изменения параметров a₁ a₂,... модели (a_i* оптимальное значение параметра a_i).

Приведенная выше схема работает хорошо, если на ее выход подаётся сигнал без помех. При наличии шума на входе ставится задача подавления помех, которую обычно решают с помощью дифференциальных схем, содержащих полосовые фильтры (дифференциальный метод).

Линеаризация. Линеаризация исходной нелинейной модели облегчает решение конкретной задачи исследования. Поэтому для упрощения моделирования и исследования, когда это возможно, желательно заменить нелинейное уравнение приближенным линейным, решение которого с достаточной степенью точности описывает свойство исходной нелинейной системы. Процесс замены нелинейной модели линейной называется линеаризацией.

Если дифференциальное уравнение объекта нелинейно из-за нелинейности его статической характеристики, то для линеаризации уравнения необходимо заменить нелинейную статическую характеристику y = F(x) линейной функцией y = a₀ + a₁x.

Основное содержание идеи линеаризации состоит в том, что различие в решениях нелинейных уравнений и их линеаризованного представления не столь существенны, чтобы приводить к недопустимым ошибкам в смысле требований к точности решения поставленной задачи.

Для линеаризации нелинейной модели y = F(x) чаще всего применяют общепринятый метод малых отклонений. Техника составления линеаризованных уравнений принципиально проста. Математическое обоснование этой процедуры заключается в требованиях к виду нелинейности функции F(x). Для допустимости линеаризации достаточно, что F(x) и 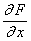существуют и непрерывны в окрестности некоторой точки (x₀, y₀). Тогда линеаризация осуществляется при помощи разложения в ряд Тейлора функции F(x, y) в окрестности точки (x₀, y₀) и отбрасыванием всех нелинейных членов этого ряда

Индекс 0 означает, что производные берутся в точке x = x₀, y = y₀.

Таким образом, исходная нелинейная модель заменяется линейной моделью вида

y = a₀ + a₁x,

где ;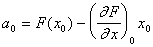

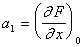
Такойспособлинеаризации означает замену кривой y = F(x) касательной в точке (x₀, y₀).

В случае многомерной модели, т.е модели вида y = F(x₁, x₂,..., x_m) получим

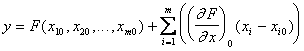
или ,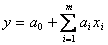

где , , 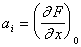i = 1,m

В этом случае гиперповерхность, описываемая нелинейной функцией 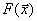в пространстве переменных x₁, x₂,..., x_m и y, заменяется гиперплоскостью, касательной к поверхности в точке (x₁₀, x₂₀,..., x_m0, y₀).

Интуитивно ясно, что линеаризованная модель, полученная при помощи разложения в ряд Тейлора, может оказаться пригодной для описания процессов в нелинейном объекте, не связанных с большими изменениями переменных в окрестности точки 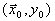. Ошибка моделирования тем меньше, чем меньше отклонения переменных.

Рассмотрим процесс линеаризации нелинейной модели при помощи разложения в ряд Тейлора на примере объекта, поведение которого описывается нелинейным дифференциальным уравнением общего вида

F(y”, y’, y, x) = 0. (4.39)

Если x₀, y₀ - некоторое установившееся состояние, то координаты x и y можно записать в виде x = x₀ + Dx, y = y₀ + Dy,

где Dx и Dy - отклонение координат x и y от установившегося состояния. Уравнение (4.39) в приращениях имеит вид

F(Dy”, Dy’, y₀ + Dy, x₀ + Dx) = 0. (4.40)

Разложим левую часть уравнения (4.40 ) в ряд Тейлора относительно точки установившегося состояния (0, 0, y₀, x₀) и пологая Dx, Dy и их производные по времени малыми, отбросим все нелинейные члены этого ряда. При этом получаем уравнение

,

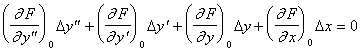которое является линейным дифференциальным с постоянными коэффициентами. Линеаризованное уравнение обычно записывают в следующем виде:

a₀Dy” + a₁Dy’ + a₂Dy = b₁Dx. (4.41)

Здесь: .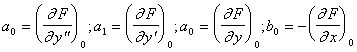

Необходимым условием линеаризации является разложимость в ряд Тейлора функции F(y”, y’, y, x) в окрестности точки, соответствующей установившемуся состоянию.

Уравнение (4.41) приближенно заменяет уравнение (4.39) лишь в некоторой малой окрестности точки (0, 0, y₀, x₀). Величина этой окрестности зависит от вида функции F(y”, y’, y, x), т.е от величин производных порядка выше первого в рассматриваемой точке. В большинстве случаев при помощи линеаризованной модели (4.41) можно исследовать поведение объекта лишь при малых отклонениях входной и выходной координаты.

Представление исходной нелинейной зависимости 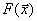в виде суммы линейных членов разложения в ряд Тейлора предполагает известным вид этой зависимости. Только в этом случае возможным окажется вычисление величин производных 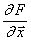. Для этого необходимо построение сложной нелинейной модели и подробное выписывание формул в общем виде с целью последующего преобразования, что усложняет процесс идентификации и увеличивают объем вычислительных работ.

Возможна линеаризация нелинейной функции 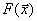при помощи секущей плоскости в многомерном пространстве, описываемой линейным уравнением

y = a₀ + a₁x₁ + a₂x₂ +... + a_mx_m,

коэффициенты которого определяются методом наименьших квадратов (МНК) так, чтобы получить хорошее приближение исходной и линеаризованной модели в некоторой области возможных изменений переменных.

Применение МНК к вычислению коэффициентов линеаризации существенным образом влияет на процедуру составления линейных уравнений. При таком подходе достаточно задаться структурой линеаризованного уравнения, т.е указать состав переменных, от которых должна зависеть исследуемая величина. Отсюда легко усматривается преимущество применения МНК для целей линеаризации: далеко не всегда можно дать точный вид функциональной связи между переменными в нелинейном виде. Для статистического подхода этого не требуется,достаточно знать даже не все, а лишь в основном определяющие переменные для описания свойств реального объекта. Это позволяет отказаться от процедуры построения нелинейных уравнений с последующим их преобразованием, так как можно сразу же отыскивать линейную связь между требуемыми по условию задачи переменными объекта.

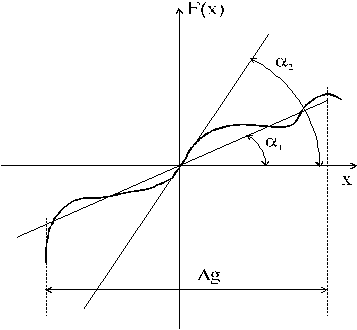
На рисунке 4.7 показана геометрическая

интерпретация

рассматриваемых способов линеаризации, где приняты следующие обозначения: a₁ - угол наклона секущей на интервале ∆D_g (линеаризация МНК ); a₂ - угол наклона касательной в точке x = 0 (линеаризация разложением в ряд Тейлора).

Из рис. 4.7 хорошо видно, что при использовании МНК обнаруживается возможность дать оценку допустимого диапазона линеаризации.

Рис.4.7

Основой для этого служит свойство МНК определять наилучшие значения искомых коэффициентов линейной модели в принятом диапазоне.

4. Упрощение модели с распределенными параметрами. Характеристики состояния объекта могут зависеть не только от времени, но и от пространственных координат. Из множества объектов с распределёнными параметрами можно выделить объекты, параметры которых приводимы к сосредоточенным. Это такие объекты, для которых достаточно знать значения входных и выходных переменных в конечном числе фиксированных точек пространства. Например, линейные объекты с распределёнными параметрами структурно могут быть представлены в виде многомерного линейного объекта с сосредоточенными параметрами. Тогда процессы в таких объектах будут описаны совокупностью математических моделей, определяющих изменения только во времени исследуемых выходных величин объектов в каждой фиксированной точке пространства.