Идентификация структуры модели

Процесс определения структуры оператора модели F составляет задачу структурной идентификации. Если же структура этого оператора определена, то процесс идентификации сводится к определению параметров этой структуры, т.е. к задаче параметрической идентификации, белее простой, чем предыдущая.

Таким образом, идентификация объекта связана прежде всего с предварительным выбором структуры модели. Под структурой модели будем понимать вид оператора F с точностью до его коэффициентов. Заметим, что структура объекта может и не совпадать со структурой модели. Например, стохастические свойства объекта обычно не отражаются в модели (модель выбирается детерминированной). Кроме того модель может иметь меньше входов и выходов, чем объект. Это часто делают при малом объеме наблюдений.

Уравнение связи между входными и выходными переменными можно записать в различной форме. Приведем некоторые общие уравнения связи между переменными.

1. Всякий одномерный статический непрерывный объект определяется функцией y = F(x). Модель этого объекта можно представить в виде разложения

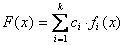(4.15)

по определенной системе функций .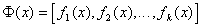

Здесь структура модели задается системой функций 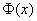и числом 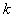, а ее параметрами являются коэффициенты разложения 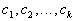. Идентификация структуры такого объекта заключается в отыскании удовлетворительной системы функций 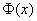, а параметрическая идентификация сводится к определению параметров 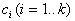при заданной системе функций.

2. Поведение детерминированного динамического одномерного объекта удобно описывать оператором

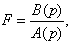(4.16)

где 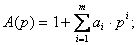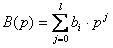, 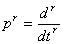- оператор дифференцирования.

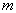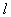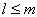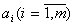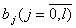Здесь структура оператора модели определяется линейностью оператора и числами и . Из физических соображений . Коэффициенты и являются неструктурными параметрами модели.

Оператор (1.16) эквивалентен обыкновенному дифференциальному уравнению вида

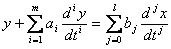(4.17)

Непрерывная модель (4.17) преобразуется в форму разностного уравнения, если отсчет времени происходит в дискретные равноотстоящие моменты. При таком отсчете времени непрерывные функции, описывающие поведение переменных, превращаются в решетчатые.

Для дискретного времени в момент времени 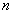разностное уравнение записывается в форме

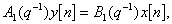(4.18)

где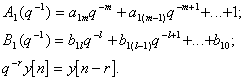

При переходе от непрерывной модели (1.17) к дискретной (1.18) порядок уравнения 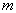и 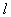сохраняются, но значения коэффициентов для непрерывной и дискретной форм моделей различны. Если известны коэффициенты в одной из форм и интервал дискретизации, значения коэффициентов в другой форме могут быть вычислены.

В теории автоматического управления широко используются также следующие записи связи между переменными на входе и выходе:

1. Интеграл свертки (интеграл Дюамеля)

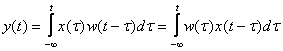, (4.19)

где - входная и выходная переменные;

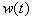- импульсная переходная (весовая) функция объекта, т.е. сигнал 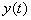на выходе объекта, если входной сигнал 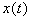представляет собой дельта-функцию .

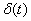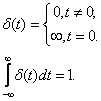
Есл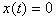и при 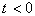, то уравнение (4.19) можно переписать в форме

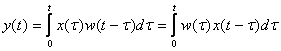. (4.20)

Для дискретного времени это уравнение записывается в форме

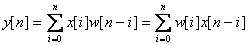. (4.21)

2. Запись связи в операторном виде

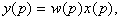
где 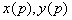- изображения по Лапласу входного и выходного сигналов;

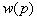- передаточная функция объекта, .

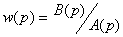В более общей форме модель динамики детерминированного нелинейного непрерывного одномерного объекта может быть представлена в виде разложения по системе операторов

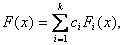
где 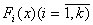-система нелинейных операторов.

Определение 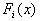является основной целью структурной идентификации. Отыскание чисел 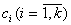составляет задачу параметрической идентификации.

Отыскание наиболее подходящей модели из множества моделей-претендентов составляет весьма важную и в тоже время достаточно трудную часть процедуры идентификации. Именно на этом этапе знание формальных свойств моделей необходимо соединить с априорным знанием, инженерным мышлением и интуицией.

При решении задач идентификации, как правило, существует две возможности выбора структуры модели. Суть одной из них заключается в том, что после тщательного изучения объекта моделирования на основе законов физики и других достоверных знаний формируется структура модели. Такие модели являются неформальными, включают неизвестные физические величины, параметрическая идентификация сводится к определению их значений. Другая возможность состоит в том, чтобы без всякого физического обоснования использовать стандартные формальные модели. Множество таких моделей, у которых параметры рассматриваются прежде всего как варьируемые средства подстройки моделей к имеющимся данным и не отражают физики процесса называется черным ящиком. Множество моделей с настраиваемыми параметрами, допускающими физическую интерпретацию, называются серыми ящиками.

Построение по возможности неформальных моделей более предпочтительно, так как они наилучшим образом отражают основные свойства реального объекта. Кроме того, построение моделей на основе анализа физических процессов в объекте позволяет составить уравнение даже на стадии проектирования объекта. Метод предполагает знание тепловых, гидравлических, пневматических, электрических процессов, процессов тепломассопереноса и химических реакций объекта.

Несмотря на большое разнообразие объектов и протекающих в них процессов, можно выделить некоторые общие подходы к составлению моделей объектов. Прежде всего следует расчленить мысленно объект на части и составить уравнение для каждой из них, заменив отброшенные части системы эквивалентными воздействиями.

Рассмотрим пример составления математической модели технологического объекта на основе изучения физических процессов.

Модель динамики резистивной печи: тепловой баланс печи резистивного нагрева складывается из изменения накопленной теплоты 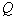, теплового потока от нагревателя 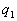и теплового потока теплопотерь 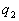вследствие теплоотдачи и конвекции:

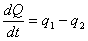, (4.24)

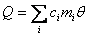, (4.25)

где 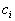-удельная теплоемкость материала 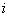- го конструктивного элемента печи;

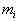-масса 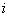-го элемента печи;

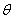-температура.

Тепловые потери 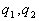в общем случае определяются формулами:

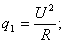
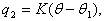(4.26)

где 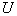— напряжение на нагревателе;

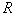— сопротивление нагревателя;

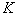— коэффициент теплопередачи;

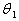— температура окружающей cреды.

Из (1.24), (1.25) и (1.26) получаем уравнение

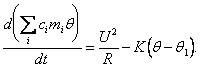(4.27)

Учитывая, что 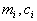постоянные величины, из (1.27) находим уравнение

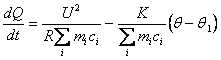, (4.28)

которое может быть линеаризовано.

Пусть 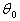-температура заданного режима нагрева, 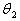-средняя температура окружающей Среды. Тогда

; ; ,

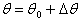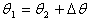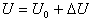где 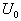-постоянное значение напряжения, необходимого для поддержания заданного постоянного значения температуры .

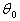В установившемся режиме

, .

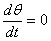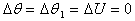Тогда из (1.28) следует

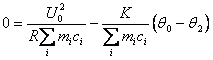. (4.29)

Вычитая (1.29) из (1.28), находим

.

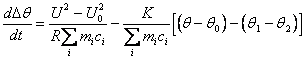Учитывая, что

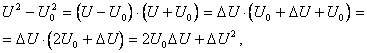
и пренебрегая величиной 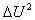, получаем

;

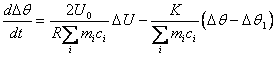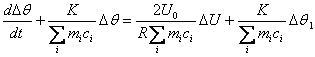. (4.30)

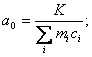
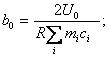
Обозначим: 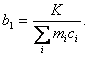(4.31)

Тогда получаем следующую модель объекта

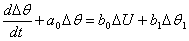, (4.32)

где 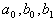-параметры модели, причем, как следует из (4.30), коэффициент 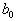зависит от режима печи (от величины ).

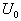При построении модели (4.32) сделано существенное предположение, что температура во всех точках печи одинакова и, следовательно, нагревательная печь является объектом с сосредоточенными параметрами.

Определение параметров модели расчетным путем по формулам (4.31) практически не представляется возможным, поскольку характеристики 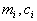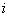-го конструктивного элемента неизвестны, а иногда трудно поддаются к учету. Отметим еще раз, что линеаризованная модель (4.32) справедлива лишь при малых значениях 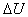(когда допустимо пренебрежение величиной 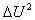). Параметры модели 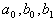теперь могут быть определены параметрической идентификацией после выбора структуры модели (4.32).