Повышение температуры кипения растворов
Рассмотрим раствор нелетучего вещества находящийся в равновесии с паром. Так как растворенное вещество нелетучее, то в паре будет находиться только растворитель. Тогда в соответствии с теоремой Гиббса химический потенциал растворителя в растворе 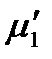 и химический потенциал чистого растворителя в паровой фазе
и химический потенциал чистого растворителя в паровой фазе 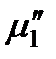 одинаковы:
одинаковы:
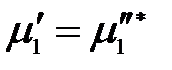
При р = const химический потенциал растворителя в растворе зависит от состава раствора и температуры, а в паровой фазе, находящейся в равновесии с раствором –только от температуры:
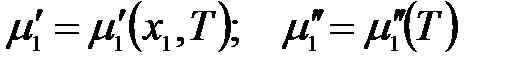 ,
,
где х1 – мольная доля растворителя в растворе.
Продифференцируем
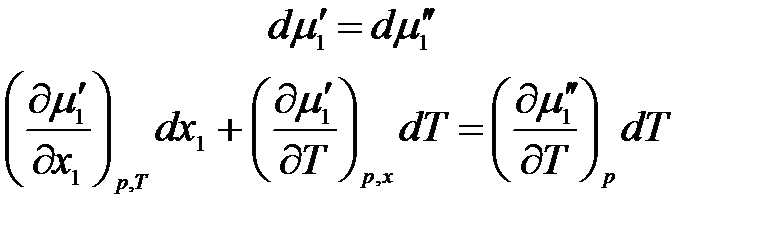 .
.
Зависимость химического потенциала компонента раствора от его состава при
Т = const выражается уравнением:
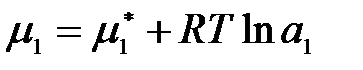 ,
,
тогда
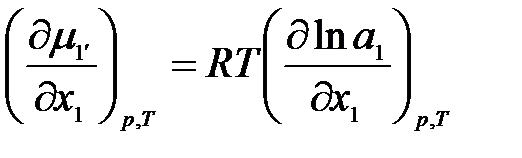 .
.
С учетом того, что при р, Т = const 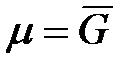 , получим:
, получим:
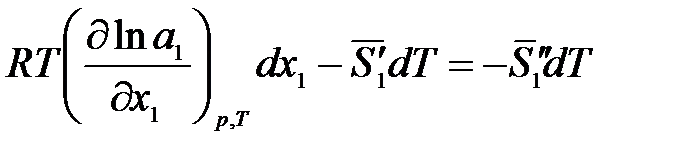 ,
,
где 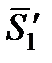 – парциальная мольная энтропия растворителя в растворе данного состава;
– парциальная мольная энтропия растворителя в растворе данного состава;
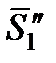 – мольная энтропия чистого растворителя в паровой фазе.
– мольная энтропия чистого растворителя в паровой фазе.
Преобразуем:
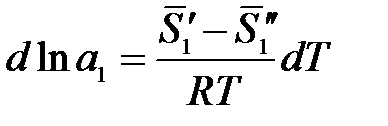 .
.
Рассмотрим разбавленный раствор твердого вещества, мольная доля растворенного вещества х2 → 0, а активность растворителя 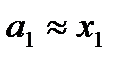 . Выразим х1 через х2 и подставим в уравнение
. Выразим х1 через х2 и подставим в уравнение
х1 = 1 – х2,
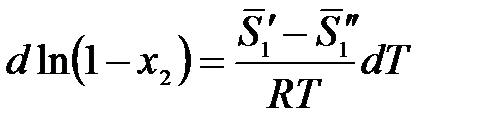 .
.
Если х2 << 1, то можно принять
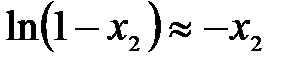 .
.
С учетом этого получим:
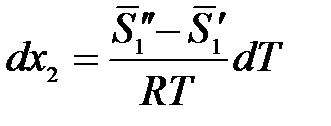
В числителе получаем парциальную мольную энтропию испарения растворителя
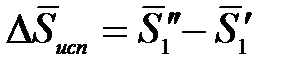 .
.
Так как раствор разбавленный, то можно принять, что парциальная мольная энтропия испарения растворителя из раствора равна мольной энтропии испарения чистого растворителя:
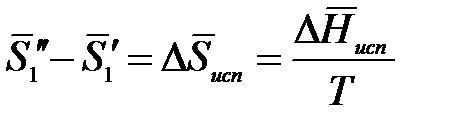 ,
,
В результате получим:
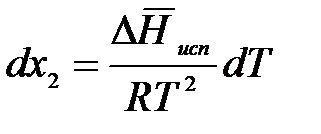 .
.
Процесс испарения идет при температуре кипения: Т = Тк = const. Пусть температура кипения чистого растворителя равна Тк0 а раствора – Тк, мольная доля растворенного вещества в чистом растворителе х2 = 0, а в растворе – х2. Проинтегрируем в интервале от Тк0 до Тк:
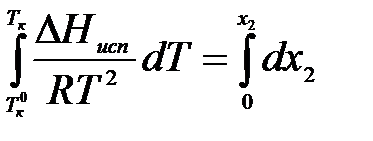 ;
;
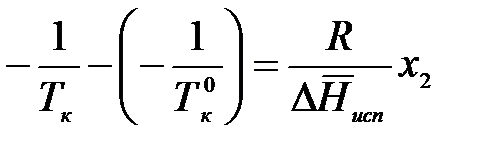 ;
;
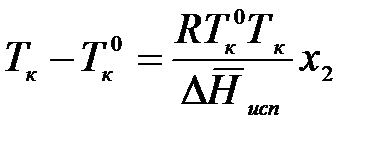
Температуры кипения Тк0 и Тк выражены в К, следовательно, 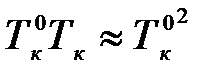 , поэтому в произведении
, поэтому в произведении  можно Тк заменить на Тк0, не вводя большой ошибки. Тогда получим
можно Тк заменить на Тк0, не вводя большой ошибки. Тогда получим
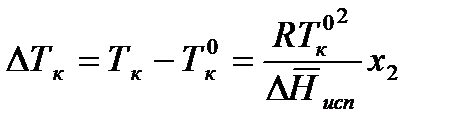
Таким образом, при р = const раствор нелетучего вещества кипит при более высокой температуре, чем чистый растворитель (рис. 2.6). Повышение температуры кипения раствора нелетучего вещества по сравнению с температурой кипения чистого растворителя прямо пропорционально мольной доле растворенного вещества. Полученное уравнение справедливо только для разбавленных растворов.
На рисунке:
Тк10 – температура кипения чистого растворителя при давлении р1;
Тк1 – температура кипения раствора при давлении р1.
Из рисунка видно, что Тк1 > Тк10.
| р |
| Т |
| О |
| п |
| ж |
| р1 |
| Тк1 |
| Тк10 |
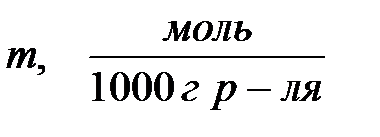
Тогда если М1 – молярная масса растворителя, а М2 – молярная масса растворенного вещества, то на 1000 г растворителя получим:
| Рис. 2.6. Повышение температуры кипения раствора по сравнению с чистым растворителем |
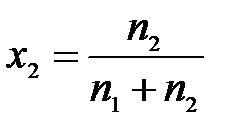 ;
; 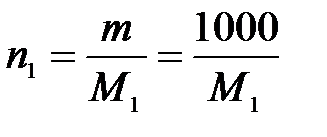 ;
; 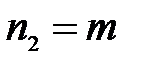 ,
,
тогда
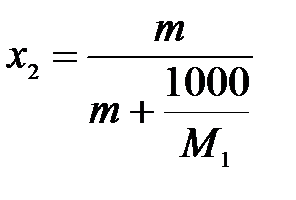 .
.
Поскольку раствор разбавлен, 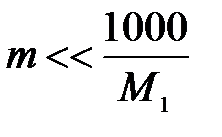
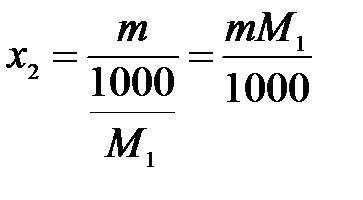 .
.
Подставим х2 в уравнение:
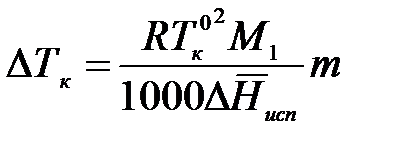 .
.
Введем обозначение:
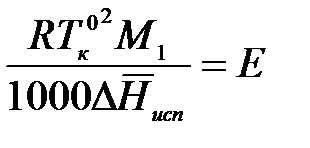 ,
,
где Е – эбулиоскопическая константа растворителя.
Тогда
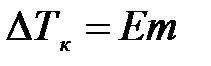 .
.
Эбулиоскопическая константа зависит от природы растворителя и не зависит от природы растворенного вещества. Физический смысл эбуллиоскопической константы: Е численно равна повышению температуры кипения раствора с концентрацией 1 моль/1000 г растворителя. Значения E для различных растворителей приведены в справочниках.
Если молекулы растворенного вещества подвергаются диссоциации, то число моль в растворе увеличивается. С учетом этого процесса уравнение для ∆Тк принимает вид:
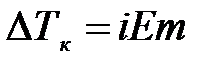 ,
,
где i – изотонический коэффициент или коэффициент Вант-Гоффа.
Коэффициент i равен отношению общего числа моль в растворе после диссоциации к числу моль растворенного вещества до диссоциации. Изотонический коэффициент можно определить по формуле:
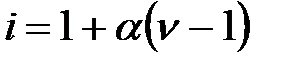 ,
,
где α – степень диссоциации электролита;
ν – число ионов, образующихся при диссоциации одной молекулы.
Физико-химические методы анализа, основанные на измерении повышения температуры кипения растворов, называются эбулиоскопическими. Эбулиоскопический метод применяется для для определения концентрации растворенного вещества, его молярной массы, изотонического коэффициента и степени диссоциации электролита. Для определения молярной массы растворенного вещества экспериментально измеряют ∆Тк раствора. Количество моль растворенного вещества в 1000 граммах растворителя, то есть моляльность можно выразить:
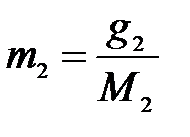 ,
,
где g2 – масса растворенного вещества.
Тогда молярная масса растворенного вещества равна:
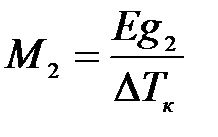 .
.
Дата добавления: 2016-06-22; просмотров: 2229;











