Тема 5. Электрические цепи с взаимно индуктивными связями

Явление взаимной индукции, взаимная индуктивность.

Если по катушке протекает переменный ток, то в пространстве вокруг нее возникает переменное магнитное поле.

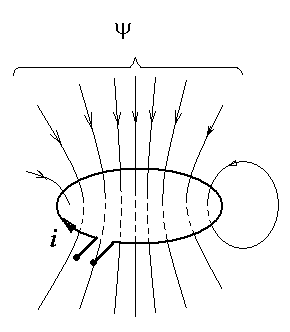
В соответствии с законом электромагнитной индукции это магнитное поле наводит в катушке ЭДС, которая препятствует изменению тока, создающего магнитное поле. Эта ЭДС называется ЭДС самоиндукции, она уравновешивается индуктивной составляющей напряжения на катушке.

Если рядом с катушкой, по которой протекает переменный ток, находится другая катушка, то в последней возникает ЭДС под действием переменного магнитного поля, созданного током первой катушки. Это явление называется взаимной индукцией, а ЭДС, наведенная током первой катушки в соседней катушке, называется ЭДС взаимной индукции.

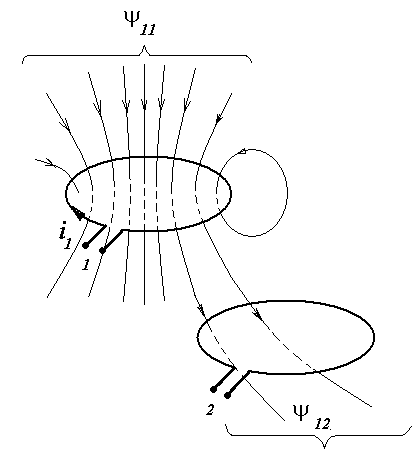
Если токи протекают через обе катушки одновременно, то в каждой из них наводятся ЭДС самоиндукции и ЭДС взаимной индукции.

5.1.2.Закон электромагнитной индукции (случай самоиндукции)

Уравнение электромагнитной индукции, как и все уравнения теории электромагнетизма, принято записывать в правовинтовой системе координат. На рис. показана одновитковая катушка, ближняя к читателю сторона катушки изображена жирной линией. Направление обхода витка (от зажима 1 к зажиму 2) и направление нормали 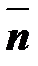к поверхности 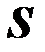, ограниченной витком, связаны правилом правого винта. Наличие у катушки нескольких витков усложнило бы рисунок, не изменяя физической картины явлений. Направления тока и ЭДС в катушке совпадают с направлением ее обхода; направление напряжения согласовано с направлением тока (оба направлены от зажима 1 к зажиму 2). Нормаль указывает направление магнитного потока.

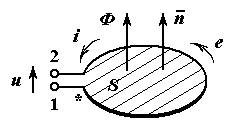
Правовинтовая система координат, связанная с одновитковой

катушкой

По закону электромагнитной индукции

,

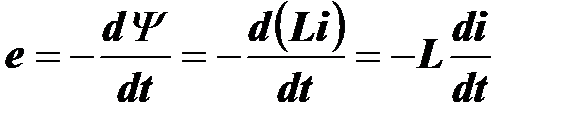где 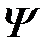- потокосцепление (полный магнитный поток) катушки; 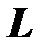- индуктивность катушки (потокосцепление пропорционально току,

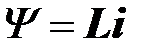). По второму закону Кирхгофа индуктивная составляющая напряжения на катушке 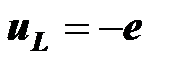, следовательно,

.

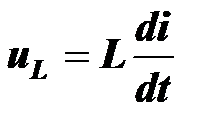Здесь не учитывается активное сопротивление провода, из которого изготовлена катушка, и, следовательно, активная составляющая напряжения. Это обстоятельство, усложняющее уравнение, будет учтено позже, а пока будем считать, что активное сопротивление катушки пренебрежимо мало.

Если по катушке протекает синусоидальный ток и напряжение на ней синусоидально, то уравнение можно представить в комплексной форме

.

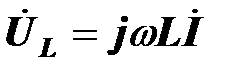Закон электромагнитной индукции (случай взаимной

индукции)

Определим ЭДС взаимной индукции во второй катушке по закону электромагнитной индукции. С каждой из катушек нужно связать правовинтовую систему координат . Часть магнитного потока 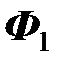, возбужденного током первой катушки 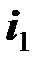, проходит сквозь вторую катушку (точнее, через поверхность 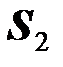, натянутую на провод, из которого изготовлена вторая катушка). Обозначим эту часть магнитного потока 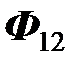, а соответствующее ему потокосцепление второй катушки в магнитном поле первой катушки через 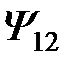. По закону электромагнитной индукции

,

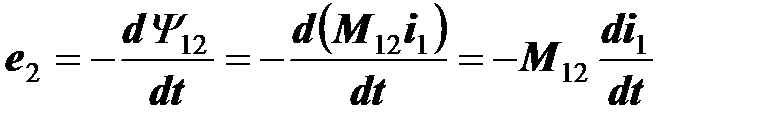где 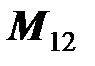- взаимная индуктивность катушек (потокосцепление 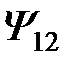пропорционально току 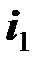, 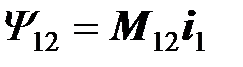). По второму закону Кирхгофа напряжение, созданное ЭДС взаимной индукции во второй катушке, равно 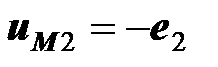, следовательно,

.

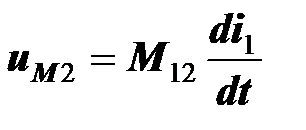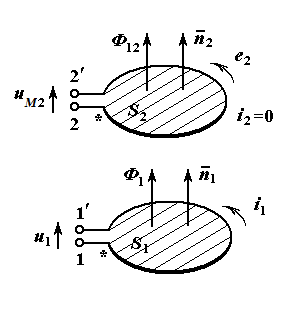
Две катушки и связанные с ними правовинтовые

системы координат

Если в первой катушке протекает синусоидальный ток, то во второй катушке возбуждается синусоидальная ЭДС и напряжение 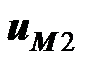синусоидально. В этом случае уравнение можно представить в комплексной форме

.

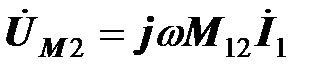Если пропустить ток через вторую катушку и определить напряжение на разомкнутых зажимах первой катушки, то получится равенство, аналогичное предыдущему с соответствующей перестановкой индексов,

.

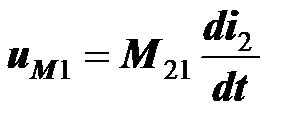В теории электромагнетизма доказано, что 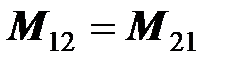, то есть любая пара катушек характеризуется одним значением взаимной индуктивности. В индексах при символе взаимной индуктивности нет необходимости.

Определение взаимной индуктивности катушек

Часть магнитного потока, созданного током одной из катушек, проходит сквозь вторую катушку . Эта часть потока пропорциональна току, возбуждающему магнитное поле. Коэффициент пропорциональности между магнитным потокосцеплением одной катушки в магнитном поле, созданном другой катушкой, и током последней катушки называется взаимной индуктивностью катушек:

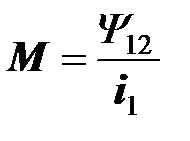или .

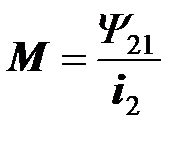Взаимная индуктивность как алгебраическая величина

Соглашение о согласовании направлений тока и напряжения на пассивном двухполюснике обеспечивает положительные значения электрического сопротивления, индуктивности и емкости основных элементов цепей. В случае двух катушек, находящихся в общем магнитном поле, ситуация усложняется: приходится согласовывать направления токов и напряжений не на одном, а на двух элементах одновременно.

Если направления токов в катушках выбраны, как показано на рисунке , то ток 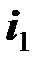и поток 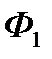(потокосцепление 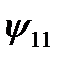) имеют одинаковые знаки в любой момент времени; поток 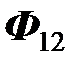(потокосцепление 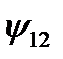)имеет такой же знак, как и поток 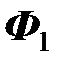, и, следовательно, тот же знак, что и ток 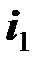. Взаимная индуктивность катушек, вычисленная по формуле,

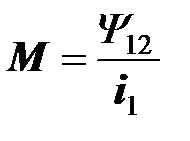
оказывается положительной величиной.

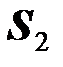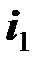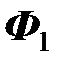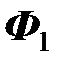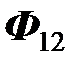Однако возможен иной выбор направлений обхода катушек, как показано на рисунке ниже. Здесь по сравнению с предыдущим изменено направление обхода второй катушки и связанное с ним направление нормали к поверхности . Ток и поток по-прежнему имеют одинаковые знаки, а потоки и отличаются знаками, потому что их направления противоположны. Взаимная индуктивность катушек получается отрицательной.

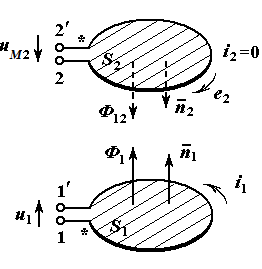
. Две катушки и связанные с ними правовинтовые системы

координат (второй вариант)

В системе двух катушек всегда можно так выбрать направления их обхода, чтобы взаимная индуктивность была положительной величиной.

В системе нескольких катушек каждая пара катушек характеризуется только ей присущей взаимной индуктивностью и может сложиться такая ситуация, что при любой комбинации направлений обхода катушек взаимные индуктивности тех или иных пар катушек оказываются отрицательными. Добиться того, чтобы все взаимные индуктивности были положительными, не удается. Положение еще более усложняется, если катушки могут поворачиваться относительно друг друга, как, например, в электродвигателе.. В описанных здесь случаях проще всего согласиться с тем, что взаимная индуктивность является алгебраической величиной, и зафиксировать ее знак в зависимости от взаимного положения правовинтовых систем координат, связанных с катушками.

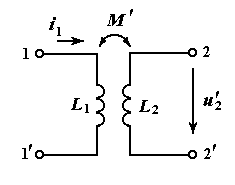
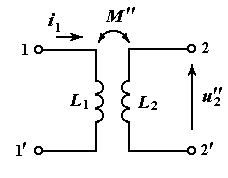
В схемах электрических цепей изображения катушек взаимной индуктивности, подобные вышеприведенным рисункам, не используются. Наличие магнитной связи между катушками (общего магнитного поля катушек) показывают двухсторонней стрелкой, как показано ниже

Изображение катушек взаимной индуктивности в схемах

электрических цепей

Теперь знак взаимной индуктивности катушек зависит от выбора направлений токов и напряжений на катушках. На рисунке выше дважды изображена одна и та же пара катушек с одним и тем же током в первой катушке 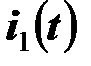, при этом 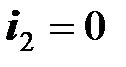. Эти схемы отличаются только направлениями напряжения на второй катушке, 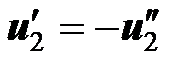. По закону электромагнитной индукции

, .

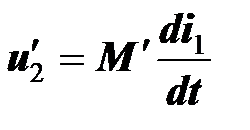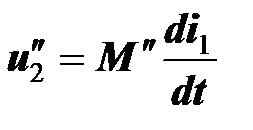Так как производная тока 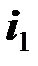одинакова в обоих выражениях, а напряжения 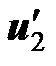и 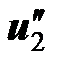отличаются только знаком, то

.

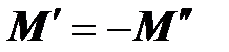Получается так, что, если заданы величина и знак взаимной индуктивности двух катушек, то должны быть указаны направления токов и напряжений на катушках. В системе нескольких катушек это привело бы к путанице, пришлось бы в каждой катушке задавать несколько направлений тока (по одному для каждой из ее магнитных связей). Возникшее затруднение легко разрешается с помощью однополярных зажимов катушек.

Однополярные зажимы катушек

Вновь обратимся к рисунку. Совсем необязательно указывать на них направления обхода катушек (направления токов и ЭДС) и направления нормалей к поверхностям, натянутым на катушки (направления магнитных токов). Достаточно пометить один из зажимов каждой катушки звездочкой.

При определении знака взаимной индуктивности катушек предполагается, что ток входит в каждую катушку через зажим, помеченный звездочкой, и направление ее собственного магнитного потока связано с направлением тока правилом правого винта.

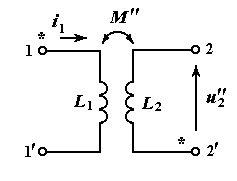
Еще раз подчеркнем, достаточно пометить зажимы катушек на выше представленном рисунке звездочками и можно опустить восемь стрелок, указывающих направления тока, ЭДС, магнитных потоков и т.д. Более того, теперь катушки с помеченными зажимами можно изобразить так, как это делается в теории электрических цепей. Помеченные зажимы называют однополярными зажимами катушек.

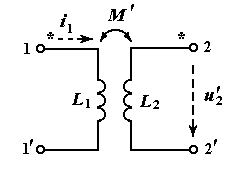
Два варианта разметки однополярных зажимов катушек

взаимной индуктивности

Первая схема на этом рисунке соответствует первой схеме предыдущего рисунка , вторая схема – второй схеме предыдущего рисунка. Разметка однополярных зажимов предопределяет направления тока 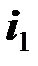и напряжений 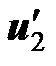на первой схеме и 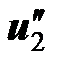на второй, потому что стрелки начинаются от помеченных зажимов. Сравнив теперь оба рисунка, приходим к выводу, что на обоих рисунках 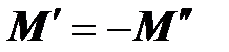. Таким образом, знак взаимной индуктивности зависит от разметки однополярных зажимов катушек.

Выбором однополярных зажимов катушек предопределяется знак их взаимной индуктивности. Если на одной из катушек перенести метку с одного зажима на другой, то взаимная индуктивность изменяет знак на противоположный

Соглашение о совпадении направлений тока и напряжения на каждой катушке остается в силе. Перенос метки с одного зажима на другой у любой катушки сопровождается одновременным изменением направлений тока и напряжения на ней. Индуктивность катушки остается положительной, а взаимная индуктивность катушек изменяет знак. Если на другой катушке также перенести метку на другой зажим, то взаимная индуктивность еще раз изменит знак. Если перенос меток сделать дважды, знак взаимной индуктивности не изменяется.

Правило знаков для напряжений взаимной индукции

Рассмотрим две катушки взаимной индуктивности, включенные в разные ветви электрической цепи . Пусть однополярные зажимы катушек размечены так, что их взаимная индуктивность положительна (для определенности). Направления токов 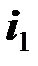и 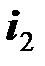были выбраны произвольно, как это обычно делается при составлении уравнений Кирхгофа.

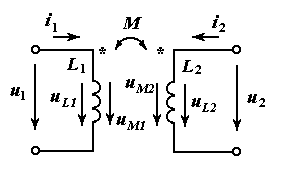
Сравнение направлений напряжений самоиндукции и взаимной индукции в катушках взаимной индуктивности

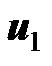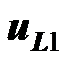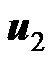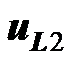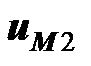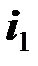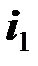Направления напряжений , и , согласованы с направлениями соответствующих токов. Направление напряжения взаимной индукции во второй катушке согласовано с направлением возбуждающего его тока . Ток входит в первую катушку через помеченный зажим, и напряжение 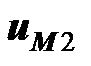направлено на второй катушке от помеченного зажима к непомеченному. Аналогичным образом напряжение взаимной индукции на первой катушке 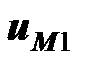согласовано с направлением тока 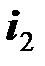. По второму закону Кирхгофа

,

.

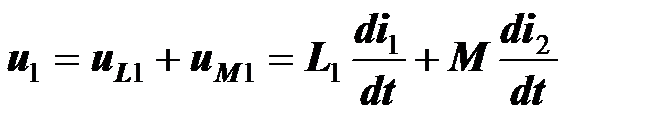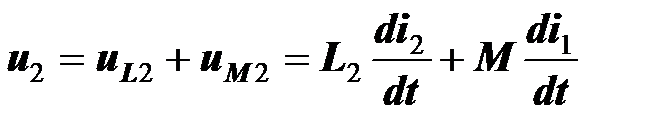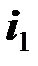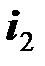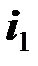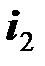На рисунке токи и направлены одинаковым образом относительно однополярных зажимов (оба тока входят в катушки через помеченные зажимы). Возможен другой вариант, когда токи и направлены различным образом относительно однополярных зажимов (один ток входит в катушку через помеченный зажим, второй ток выходит из катушки через помеченный зажим) .

Сравнение направлений напряжений самоиндукции и взаимной индукции в катушках взаимной индуктивности (второй вариант)

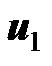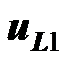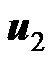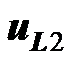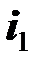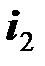Здесь, как всегда, направления напряжений , и , согласованы с направлениями токов и соответственно. По сравнению с предыдущим рисунком изменились направления напряжени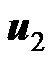й и 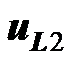вследствие изменения направления тока 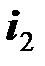. Направление напряжения взаимной индукции во второй катушке 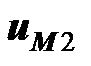согласовано с направлением тока 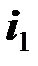. Направление тока 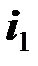осталось таким же, поэтому сохранилось без изменения направление напряжения 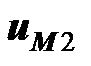. Направление напряжения взаимной индукции в первой катушке 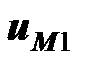согласовано с направлением тока 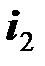(этот ток выходит из помеченного зажима второй катушки и напряжение 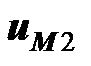направлено от непомеченного к помеченному зажиму первой катушки). По сравнению с предыдущей схемой ток 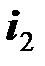изменил направление, и изменилось направление индуцированного им напряжения 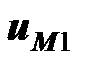. Напряжения на катушках определим по второму закону Кирхгофа:

,

.

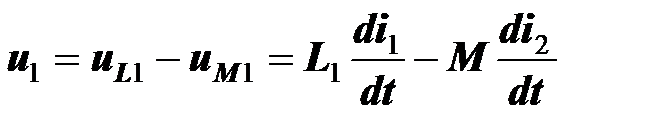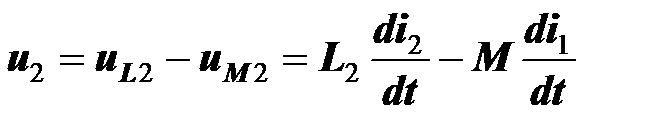На основании уравнений (5.7) и (5.8) можно сформулировать правило знаков для напряжений взаимной индукции.

Правило знаков. Если токи в катушках взаимной индуктивности направлены одинаковым образом относительно однополярных зажимов, то напряжения самоиндукции и взаимной индукции каждой из катушек имеют одинаковые знаки. Если токи в катушках направлены различным образом относительно однополярных зажимов, то знаки перед напряжениями самоиндукции и взаимной индукции различны.

В ходе записи уравнений, составляемых по второму закону Кирхгофа, напряжение, возбуждаемое в каждой катушке переменным магнитным полем, нужно делить на две составляющие: напряжение самоиндукции и напряжение взаимной индукции. Сначала определяется знак перед напряжением самоиндукции (при этом направление напряжения самоиндукции, как обычно, сравнивается с направлением обхода контура, для которого составляется уравнение второго закона Кирхгофа). Затем по правилу знаков определяется знак перед напряжением взаимной индукции.

В системе нескольких катушек взаимной индуктивности напряжение на каждой катушке нужно разделить на несколько составляющих: напряжение самоиндукции и напряжения взаимной индукции по числу катушек, имеющих магнитную связь с рассматриваемой катушкой. Знак перед каждым из напряжений взаимной индукции определяется по правилу знаков.

Последовательное включение катушек взаимной индуктивности

Согласное включение катушек

Говорят, что две последовательно соединенных катушки взаимной индуктивности включены согласно, если ток направлен одинаковым образом относительно однополярных зажимов (как бы ни было выбрано направление тока) .. В схеме замещения учтены активные сопротивления катушек.

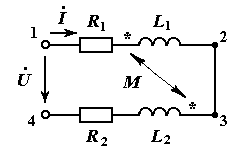
Согласное включение катушек взаимной индуктивности

Процесс, происходящий в электрической цепи, описывается уравнением, составленным по второму закону Кирхгофа,

+ = .

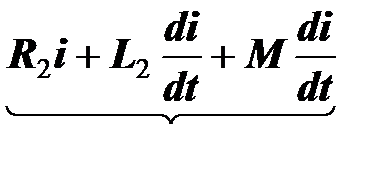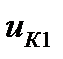
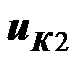
Первая тройка слагаемых дает в сумме напряжение 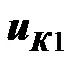на первой катушке (между зажимами 1 и 2 на рис. ), вторая тройка – напряжение 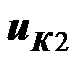на второй катушке (между зажимами 3 и 4). Знаки перед напряжениями самоиндукции и взаимной индукции у каждой из катушек совпадают, так как ток направлен одинаковым образом относительно однополярных зажимов .

Представим последнее уравнение в комплексной форме

.

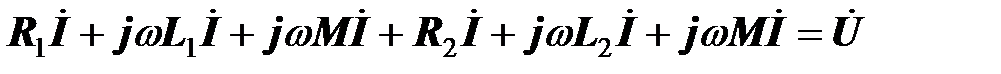Из него находим ток

.

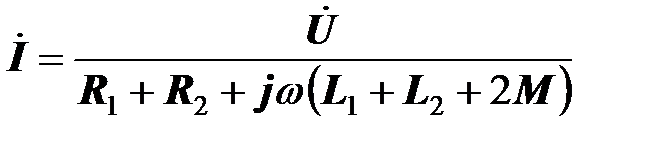Комплексное сопротивление двух согласно включенных катушек взаимной индуктивности равно

.

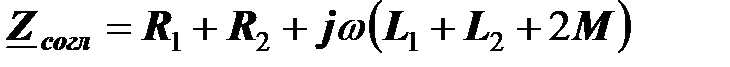Эквивалентное индуктивное сопротивление

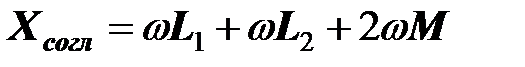
На векторной диаграмме, построенной при предположении положительного знака взаимной индуктивности катушек при выбранной маркировке зажимов инуктивно связанных катушек, показаны все напряжения, входящие в уравнение , а также напряжения на обеих катушках 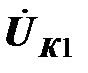и 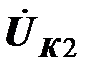. Векторы напряжений привязаны к вектору тока 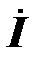, с которого начинается построение диаграммы. Напряжения взаимной индукци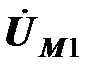и и 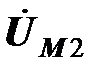одинаковы в обеих катушках.

Векторная диаграмма тока и напряжений для согласно включенных катушек взаимной индуктивности ( при М > 0)

Встречное включение катушек

После опыта с согласно включенными катушками включим их так чтобы немаркировочный зажим одной катушки был подключен к немаркировочному зажиму другой катушки, оставляя включение катушек в схеме последовательным. Такое включение катушек взаимной индуктивности называют встречным.

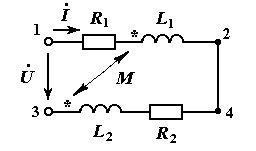
Встречное включение катушек взаимной индуктивности

Режим электрической цепи описывается уравнением Кирхгофа в комплексной форме

.

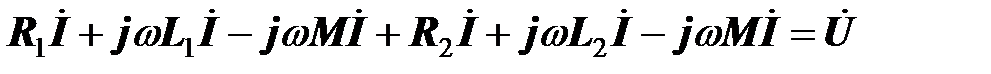Три первых слагаемых в сумме дают напряжение на первой катушке, три последних – напряжение на второй катушке. Знаки перед напряжениями самоиндукции и взаимной индукции у каждой из катушек противоположны, так как ток направлен различным образом относительно однополярных зажимов.

Комплексный ток в рассматриваемой цепи равен

.

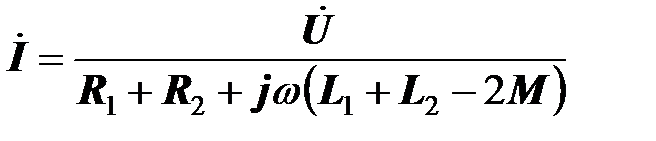Комплексное сопротивление двух встречно включенных катушек взаимной индуктивности равно

.

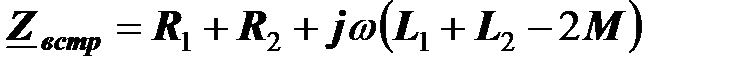Эквивалентное реактивное сопротивление

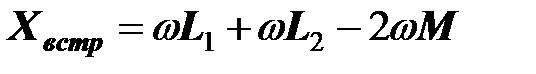
На векторной диаграмме ниже (при положительном знаке М) показаны напряжения, входящие в уравнение, а также напряжения на катушках 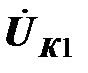и 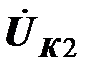. Активные составляющие напряжений изображаются векторами, параллельными вектору тока 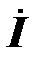, реактивные составляющие – векторами, перпендикулярными вектору тока. Напряжения взаимной индукци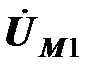и и 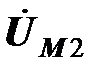одинаковы, соответствующие им векторы направлены навстречу векторам напряжени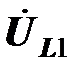й и .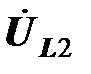

Векторная диаграмма тока и напряжений для встречно включенных катушек взаимной индуктивности (М > 0)

Измерение величины и знака взаимной индуктивности катушек

Допустим, что в наличии имеются две катушки взаимной индуктивности, зажимы которых доступны для присоединения источника переменного синусоидального и постоянного напряжений и измерительных приборов (амперметра, вольтметров электромагнитной и магнитоэлектрической систем, ваттметра). Требуется определить взаимную индуктивность катушек.

Предварительно определим (по измеренным значениям напряжения, тока, мощности при синусоидальном источнике) активное сопротивление и индуктивность каждой катушки,

, , ,

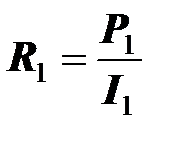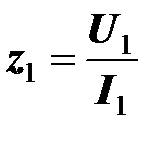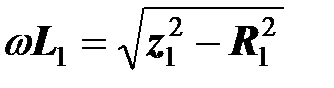где 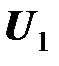- напряжение на зажимах первой катушки; 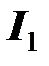- ее ток, 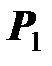- потребляемая ею мощность; 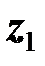- полное сопротивление катушки. Аналогично определяются параметры второй катушки.

Затем проведем опыты с аналогичными измерениями при согласном и встречном включении катушек.

Эквивалентные реактивные сопротивления двухполюсников будут равны

, ,

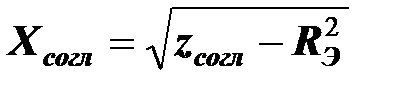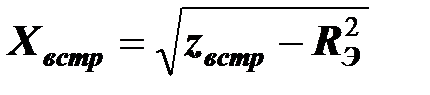где 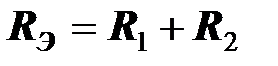- эквивалентное активное сопротивление двухполюсников.

Если воспользоваться выражениями, полученными для согласного и встречного включения выше, то не трудно установить, что

,

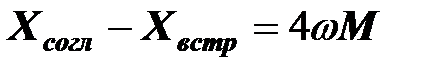то есть

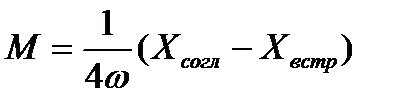
С помощью этой формулы можно вычислить взаимную индуктивность катушек по величине и знаку.

Воздушный трансформатор

Уравнения трансформатора

Трансформатор состоит из двух катушек взаимной индуктивности, к одной из которых присоединяется источник переменного напряжения, к другой приемник электрической энергии .

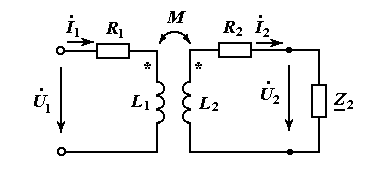
Схема замещения трансформатора

Цепь, в которую включен источник, называется первичной; цепь, содержащая приемник с комплексным сопротивлением 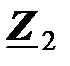, называется вторичной цепью. Электрическая энергия поступает из первичной цепи во вторичную через магнитное поле, связывающее катушки трансформатора в единое целое. В большинстве трансформаторов катушки помещаются на магнитный сердечник, который намагничивается токами, протекающими в катушках, и усиливает их магнитное поле. Благодаря этому многократно увеличиваются индуктивности и взаимная индуктивность катушек, возрастает мощность, передаваемая из первичной цепи во вторичную.

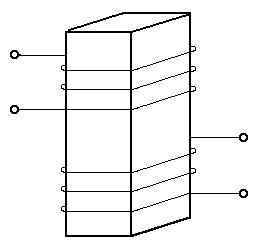
Магнитный поток в сердечнике трансформатора не пропорционален токам, точнее, зависимость потока от токов нелинейна. При больших токах рост магнитного потока при дальнейшем увеличении токов замедляется или прекращается совсем, способность сердечника к дальнейшему намагничиванию оказывается исчерпанной, наступает магнитное насыщение сердечника. Индуктивности и взаимная индуктивность катушек изменяются при изменении токов, в схеме замещения трансформатора появляются нелинейные элементы, ее анализ существенно усложняется. Однако у многих трансформаторов в нормальном (неаварийном) диапазоне изменения токов, а также у трансформаторов с незамкнутыми магнитными сердечниками (рис. 5.13) или вообще без магнитных сердечников индуктивности и взаимные индуктивности катушек являются практически постоянными величинами. Электрические цепи с такими трансформаторами относятся к линейным цепям. Существует и класс трансформаторов с немагнитными сердечниками. Магнитные свойства таких сердечников практически совпадают с магнитными свойствами воздуха. Такие трансформаторы называют воздушными. Теория таких трансформаторов (линейная теория) излагается в этом параграфе.

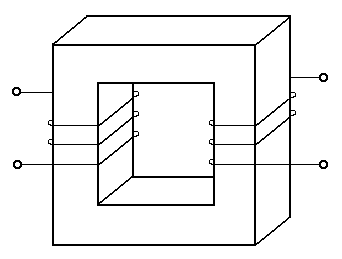
Трансформатор с замкнутым сердечником (слева) и

незамкнутым сердечником (справа)

Режим работы трансформатора описывается уравнениями, составленными по второму закону Кирхгофа для первичного и вторичного контуров,

,

.

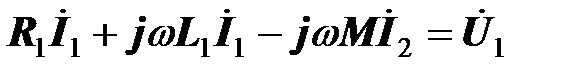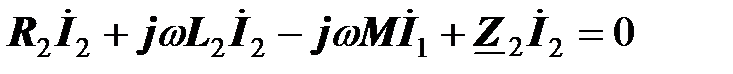Знаки перед напряжениями самоиндукции и взаимной индукции различны, так как токи в катушках направлены различным образом относительно однополярных зажимов (ток 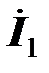входит в первую катушку через маркировочный зажим, ток 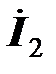выходит из второй катушки через маркировочный зажим).

Найдем ток 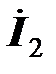из второго уравнения и полученное выражение подставим в первое уравнение:

,

.

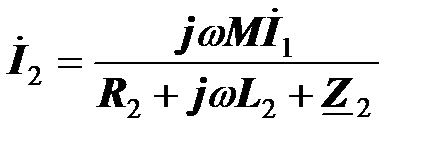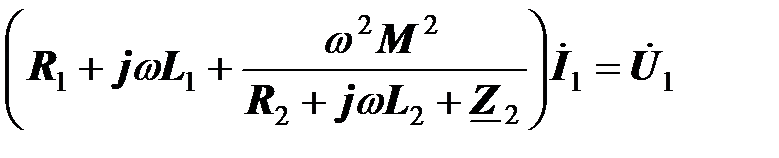Множитель перед входным током 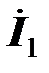представляет собой входное комплексное сопротивление трансформатора

.

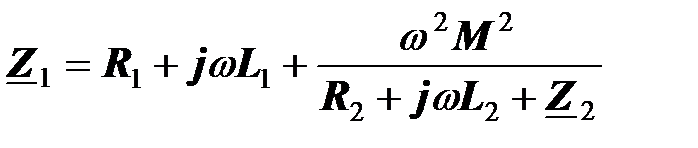В режиме холостого хода, когда ток 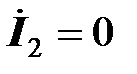, первое уравнение трансформатора принимает вид

,

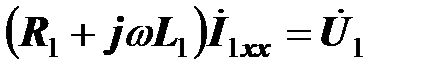следовательно, входное сопротивление трансформатора на холостом ходу равно комплексному сопротивлению первичной катушки

.

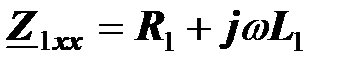В рабочем режиме, как следует из формулы, к сопротивлению холостого хода добавляется комплексное сопротивление

,

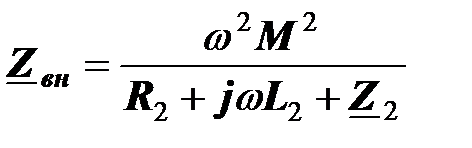которое вторичная цепь вносит в первичную цепь.

Входное сопротивление трансформатора складывается из сопротивления первичной катушки (сопротивления холостого хода 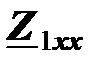) и сопротивления, вносимого вторичной цепью. Вносимое сопротивление (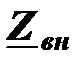)равно отношению квадрата сопротивления взаимной индукции ( 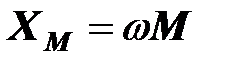) к комплексному сопротивлению вторичной цепи.

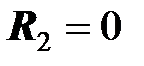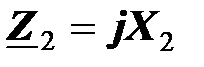Рассмотрим частный случай, когда и , где 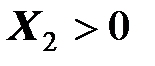. При этом согласно уравнению (5.13)

.

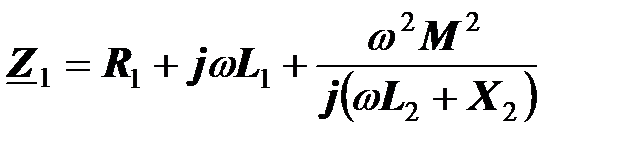После подключения к трансформатору индуктивного сопротивления 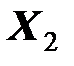реактивная составляющая входного сопротивления

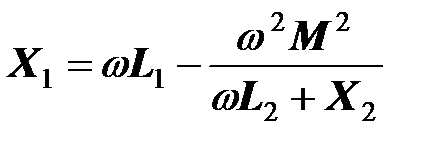
уменьшается. Следовательно, после включения нагрузки трансформатора его первичный ток увеличивается.

Этот вывод, полученный для простого частного случая, остается справедливым в большинстве ситуаций, встречающихся на практике. Исключения возможны, когда нагрузка трансформатора имеет емкостный характер ( ).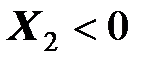

Векторная диаграмма трансформатора

Начнем построение диаграммы с вектора вторичного тока 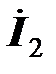, который направим по оси действительных. Допустим, что сопротивление нагрузки 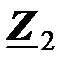имеет активно - индуктивный характер, значит, 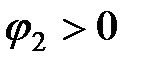. Прибавив к напряжению на нагрузке 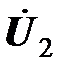активную и индуктивную составляющие напряжения на вторичной катушке, получаем согласно второму уравнению трансформатора, что

.

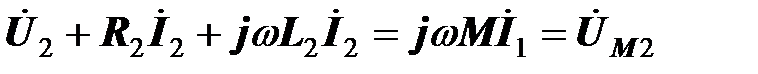Алгебраическая сумма напряжений самоиндукции и взаимной индукции во втором уравнении трансформатора представляет собой ЭДС, индуцированную во второй катушке (взятую с противоположным знаком, так как ЭДС и напряжения отсчитываются в одном направлении)

.

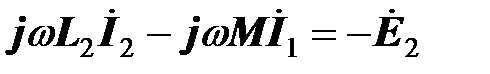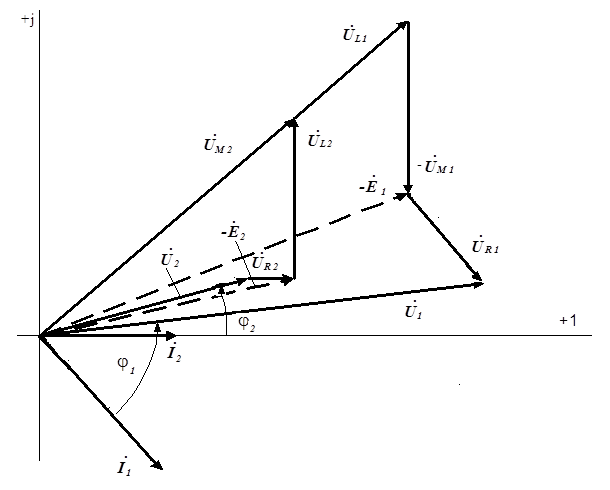
Векторная диаграмма токов и напряжений трансформатора

Вектор 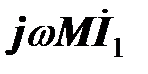опережает вектор 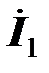на 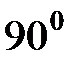(на диаграмме опережение соответствует повороту против часовой стрелки), следовательно, вектор 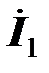отстает на 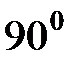от вектора 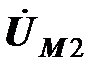. Это заключение позволяет нанести на диаграмму вектор первичного тока .

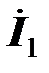Далее к индуктивной составляющей напряжения на первичной катушке прибавим напряжение 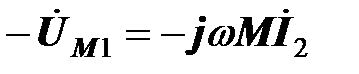, вектор которого перпендикулярен вектору тока 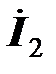и направлен вдоль оси мнимых вниз. Сумма векторов напряжени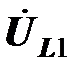й и 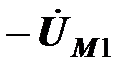в первом уравнении трансформатора дает ЭДС, индуцированную в первичной катушке, взятую с противоположным знаком,

.

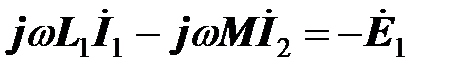Прибавив к ЭДС ( 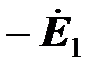) активную составляющую напряжения на первичной катушке, получаем согласно первому уравнению трансформатора

.

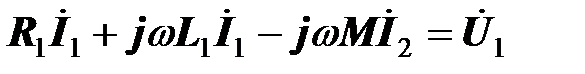Наконец, отметим угол 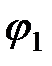между векторами тока 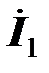и напряжения .

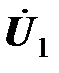Эквивалентная схема замещения трансформатора с развязкой магнитных связей

Сначала выполним довольно простые эквивалентные преобразования уравнений трансформатора

,

,

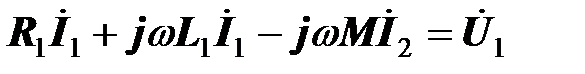а затем построим схему замещения, соответствующую преобразованным уравнениям.

Прибавим и одновременно вычтем из первого уравнения дополнительное слагаемое :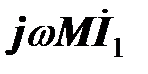

;

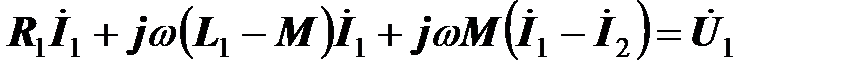ко второму уравнению прибавим и одновременно вычтем из него дополнительное слагаемое :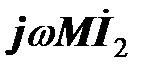

.

Введем сокращенное обозначение

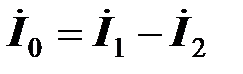
и, учитывая его, перепишем уравнения трансформатора

,

.

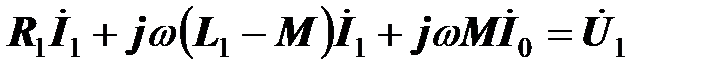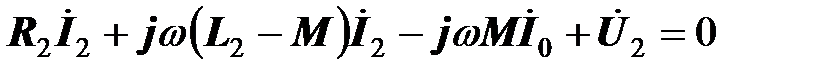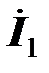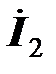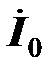Полученная система уравнений Кирхгофа соответствует цепи с двумя узлами и двумя независимыми контурами, в цепи три ветви с токами , и . В первой ветви содержится комплексное сопротивление 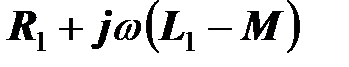, во второй ветви – комплексное сопротивление 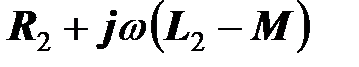и сопротивление нагрузки, в третьей ветви, общей для двух контуров, - сопротивление 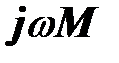. Схема замещения этой цепи показана на рисунке.

Полученные уравнения эквивалентны исходным исходным уравнениям трансформатора, следовательно, и схемы трансформатора, представленные на рисунках эквивалентны . В последней схеме отсутствуют катушки взаимной индуктивности, в ней нет в явном виде магнитной связи между первичной и вторичной катушками. Такие эквивалентные схемы называют схемами с исключенной (развязанной) магнитной связью. Именно такие схемы замещения трансформатора применяются в электротехнике и электронике. Эквивалентная схема замещения имеет по сравнению с исходной схемой ряд преимуществ, главное из которых заключается в том, что ненужно разбираться со знаками взаимной индуктивности и напряжений взаимной индукции.

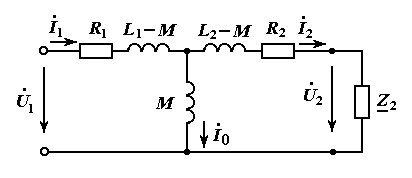
Эквивалентная схема замещения трансформатора с развязкой магнитных связей

Совершенный и идеальный трансформаторы

Идеальный трансформатор обеспечивает передачу электрической энергии из источника в приемник без потерь и без рассеивания ее в окружающем пространстве. Для этого необходимо выполнение двух условий: 1) в трансформаторе нет потерь электрической энергии, значит, 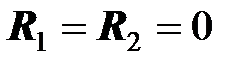; 2) магнитный поток, созданный первичным током, полностью сцеплен со вторичной катушкой (соответственно, магнитный поток, созданный вторичным током полностью сцеплен с первичной катушкой).

Запишем уравнения трансформатора для этого идеального случая:

,

.

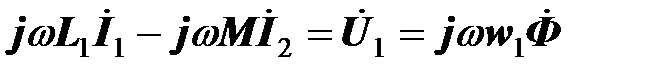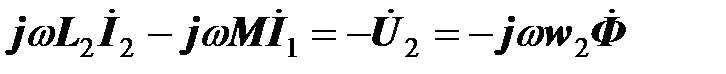Последние члены в этих соотношениях показывают, что ЭДС, уравновешивающие напряжения 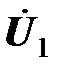и 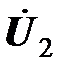, наводятся в первичной и вторичной катушках одним и тем же магнитным потоком 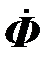; потокосцепления катушек равны

,
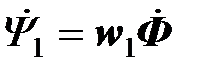