Тема 8. Переходные процессы в линейных электрических цепях
Любое включение, отключение или переключение в электрической цепи называется коммутацией. После коммутации, как правило, в цепи возникает переходный процесс, который продолжается в течение небольшого промежутка времени. После прекращения переходного процесса наступает установившийся режим. В цепях с источниками постоянного напряжения в установившихся режимах протекают постоянные токи, а в цепях с источниками синусоидального напряжения - синусоидальные токи.
Переходные процессы протекают в цепях, содержащих реактивные элементы. В течение переходного процесса происходит перераспределение энергии между реактивными элементами. После того как эта энергия рассеивается на сопротивлениях схемы (на резисторах) переходный процесс прекращается и наступает установившейся режим.
Процесс перехода ЭЦ из одного установившегося состояния в другое называется переходным процессом.
Коммутация в ЭЦ осуществляется коммутирующим ключом. В электрических схемах условное изображение коммутирующих ключей имеет вид
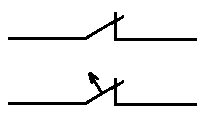
Коммутация на отключение элемента цепи
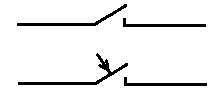
Коммутация на включение элемента цепи
Момент коммутация соответствует значению времени t =0
Различают момент предшествующий коммутации t = -0 и момент после коммутации t = +0=0
Коммутирующий ключ называется идеальным, если длительность процесса коммутации равна нулю.
Значения всех токов и напряжений в момент коммутации могут изменяться скачком (но возможны и случаи сохранения до коммутационных значений ). Эти значения называются начальными и обозначаются как i(0), u(0).
Для тока в индуктивности и напряжения на емкости справедливы законы коммутации, в соответствии с которыми:
Ток в индуктивности в момент коммутации непрерывен (первый закон коммутации)
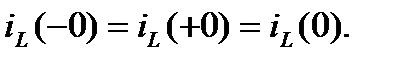
Напряжение на ёмкости в момент коммутации непрерывно (второй закон коммутации)
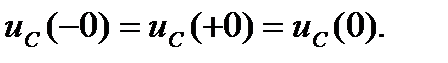
Законы коммутации можно объяснить, приняв во внимание выражения для энергии, запасённой в магнитном поле катушки,
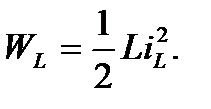
и в электрическом поле конденсатора
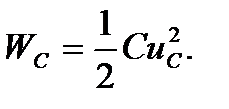
Скачкообразное изменение тока в индуктивности и напряжения на емкости невозможно из-за необходимости источников энергии бесконечной мощности.
Значения тока в индуктивности и напряжения на емкости в момент коммутации называются независимыми начальными условиями. Все остальные значения токов, напряжений и их производных по времени в момент коммутации называются зависимыми начальными условиями.
Расчет переходных процессов предполагает решение уравнений Кирхгофа для мгновенных токов и напряжений в электрической цепи после коммутации. Уравнения Кирхгофа для мгновенных токов и напряжений представляют из себя системудифференциальных уравнений .
Для решения такой системы можно использовать:
- классический (метод Коши)
- операторный
методы расчета переходных процессов.
Классический метод расчета переходных процессов
Систему уравнений Кирхгофа, описывающую переходный процесс в линейной электрической цепи, можно свести к одному дифференциальному уравнению относительного одного из токов или напряжений цепи. В общем виде это уравнение записывается следующим образом:
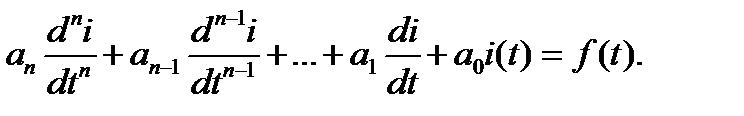
Здесь 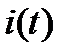 – переходный ток в к-ой ветви, постоянные
– переходный ток в к-ой ветви, постоянные 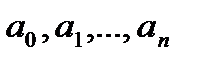 зависят от параметров пассивных элементов цепи и способа их соединения,
зависят от параметров пассивных элементов цепи и способа их соединения, 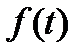 –известная функция, которая кроме параметров пассивных элементов зависит от ЭДС и токов источников, включённых в цепь. При отсутствии источников в цепи (в задачах на отключение)
–известная функция, которая кроме параметров пассивных элементов зависит от ЭДС и токов источников, включённых в цепь. При отсутствии источников в цепи (в задачах на отключение) 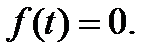 В цепи с источниками постоянного напряжения
В цепи с источниками постоянного напряжения 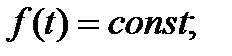 в цепи с источниками синусоидального напряжения
в цепи с источниками синусоидального напряжения 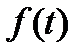 – синусоидальная функция времени.
– синусоидальная функция времени.
Общее решение дифференциального уравнения с постоянными коэффициентами (а, следовательно, и системы уравнений Кирхгофа) состоит из частного решения, которое зависит от вида функции 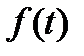 , т.е. источников электрической энергии, и общего решения однородного дифференциального уравнения, которое получается из исходного уравнения заменой правой части
, т.е. источников электрической энергии, и общего решения однородного дифференциального уравнения, которое получается из исходного уравнения заменой правой части 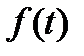 на нуль:
на нуль:
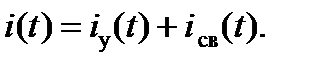
В последнем равенстве 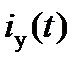 –частное решение дифференциального уравнения , в электротехнике оно называется установившейся (принужденной) составляющей тока, или просто установившимся (принужденным) током;
–частное решение дифференциального уравнения , в электротехнике оно называется установившейся (принужденной) составляющей тока, или просто установившимся (принужденным) током; 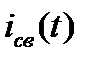 –решение однородного дифференциального уравнения, соответствующего уравнению , в электротехнике оно называется свободной составляющей переходного тока, или свободным током.
–решение однородного дифференциального уравнения, соответствующего уравнению , в электротехнике оно называется свободной составляющей переходного тока, или свободным током.
Установившейся ток 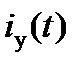 протекает в к-ой ветви под действием источников электрической энергии, он сохраняется в цепи после прекращения переходного процесса, т.е. в установившемся режиме. Свободные токи протекают в цепи, в которой нет источников электрической энергии
протекает в к-ой ветви под действием источников электрической энергии, он сохраняется в цепи после прекращения переходного процесса, т.е. в установившемся режиме. Свободные токи протекают в цепи, в которой нет источников электрической энергии 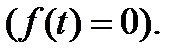 Они существуют в течение ограниченного промежутка времени, пока не прекратится обмен энергией между реактивными элементами, вызванный дисбалансом распределения энергии между ними в момент коммутации. После прекращения свободных токов переходный процесс заканчивается и наступает установившейся режим.
Они существуют в течение ограниченного промежутка времени, пока не прекратится обмен энергией между реактивными элементами, вызванный дисбалансом распределения энергии между ними в момент коммутации. После прекращения свободных токов переходный процесс заканчивается и наступает установившейся режим.
Общее решение однородного дифференциального уравнения с постоянными коэффициентами представляется в виде
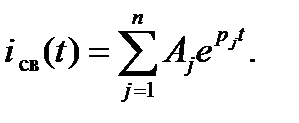
Таким образом, решение дифференциального уравнения для тока в любой ветви цепи записывается в виде
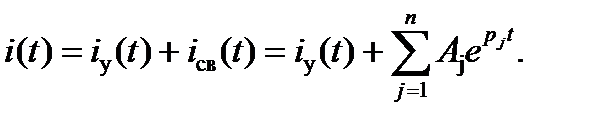
Описанный метод расчета переходных токов в математике называют метод Коши и он является классическим методом расчета переходных процессов в электрических цепях
В формуле решения для тока 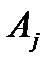 –постоянные интегрирования, которые определяются с помощью начальных условий и различны для токов разных ветвей;
–постоянные интегрирования, которые определяются с помощью начальных условий и различны для токов разных ветвей; 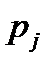 –корни характеристического уравнения, соответствующего дифференциальному уравнению.
–корни характеристического уравнения, соответствующего дифференциальному уравнению.
Характеристическое уравнение получается, если свести систему уравнений Кирхгофа к одному уравнению для одного из токов цепи. Но такой способ составления характеристического уравнения нецелесообразен, так как обычно это связано с громоздкими математическими выкладками. В случае сложной цепи применяют два других способа вывода характеристического уравнения.
Универсальный способ. Из коэффициентов системы уравнений Кирхгофа для схемы после коммутации составляется определитель и приравнивается к нулю. Например, для схемы
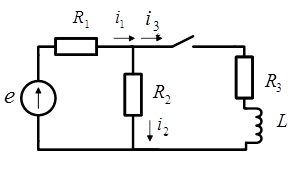
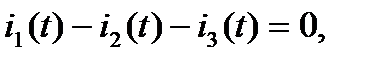
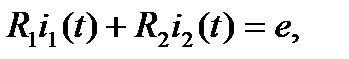
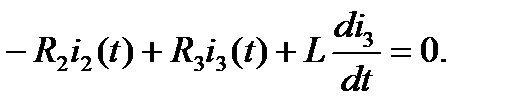
Определитель системы уравнений имеет вид:
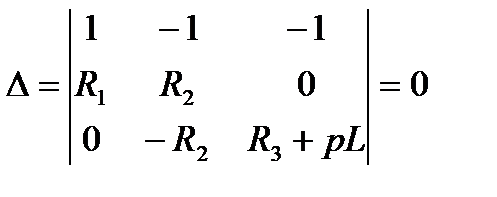 .
.
Здесь оператор дифференцирования 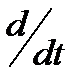 заменён искомой переменной
заменён искомой переменной 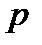 . Раскроем определитель по элементам первой строки:
. Раскроем определитель по элементам первой строки:
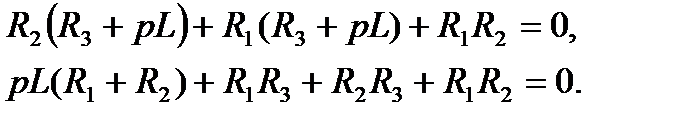
Из последнего уравнения находим
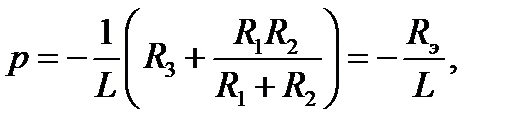
где 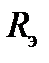 - сопротивление части цепи, состоящей из резисторов, относительно зажимов индуктивности L (после исключения из цепи источника ЭДС резисторы
- сопротивление части цепи, состоящей из резисторов, относительно зажимов индуктивности L (после исключения из цепи источника ЭДС резисторы 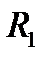 и
и 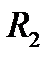 включены параллельно, а
включены параллельно, а 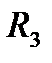 включён последовательно с группой параллельно соединённых резисторов).
включён последовательно с группой параллельно соединённых резисторов).
Равенство определителя нулю – это алгебраическое уравнение, корни которого являются показателями экспоненциальных составляющих свободных токов.
Примечание к составлению определителя. Если в цепи имеется конденсатор, то в уравнении, составленном по второму закону Кирхгофа, появится оператор интегрирования. Его нужно заменить в определителе множителем 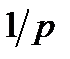 , точнее
, точнее
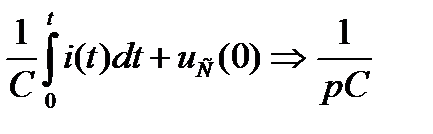
(символ 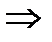 можно прочитать как “даёт коэффициент”).
можно прочитать как “даёт коэффициент”).
Способ третий: с помощью операторного сопротивления цепи (для цепей со смешанным соединением ветвей).
Запишем комплексное сопротивление цепи, возникшей после коммутации, относительно зажимов источника :
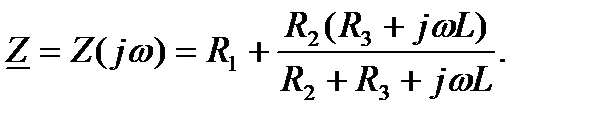
Заменив мнимую величину 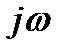 комплексной переменной
комплексной переменной 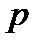 , получим операторное сопротивление
, получим операторное сопротивление
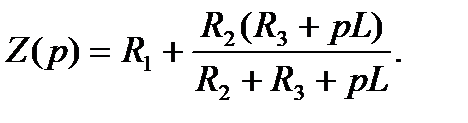
Приравняем операторное сопротивление цепи нулю. Основанием для этого может служить то обстоятельство, что свободные токи протекают в цепи без источников электрической энергии и сопротивление цепи этим токам должно быть нулевым (при нулевом напряжении и ненулевом сопротивлении ток невозможен).
Таким образом, характеристическое уравнение имеет вид
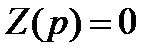 .
.
После элементарных алгебраических преобразований получается 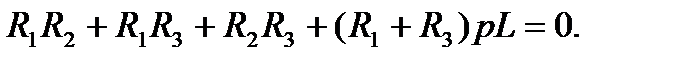
что совпадает с результатами универсального способа.
Порядок системы уравнений Кирхгофа и эквивалентного ей одного дифференциального уравнения равен степени характеристического уравнения и равен числу экспоненциальных составляющих свободного тока в выражении для решения и обычно равен числу реактивных элементов в цепи.
Порядок расчета переходных процессов в электрических цепях классическим методом
1.Нарисовать схему после коммутации и составить для нее уравнения Кирхгофа
2.Составить выражение для характеристического уравнения, найти его корни
3.Записать общий вид решения для переходного процесса по виду корней характеристического уравнения
4.Рассчитать установившийся (принужденный) режим в схеме после коммутации
5.Рассчитать независимые начальные условия (ННУ) по схеме до коммутации
6.Рассчитать зависимые начальные условия (ЗНУ) по схеме после коммутации
7.Определить постоянные интегрирования решения переходного процесса
8.Записать окончательное выражение решения и построить его график
Примеры расчёта и анализа переходных процессов в цепях первого порядка.
Пример 1
Цепь с одним реактивным элементом (цепь первого порядка)
1. Нарисовать схему после коммутации и составить для нее уравнения Кирхгофа
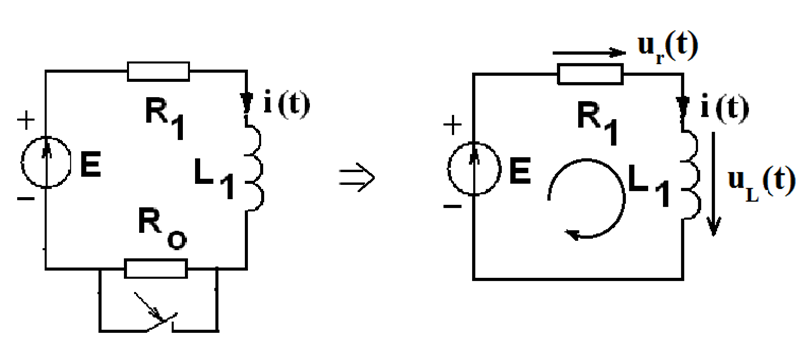
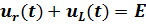
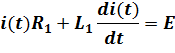
2. Составить выражение для характеристического уравнения, найти его корни
Характеристическое уравнение может быть найдено по виду схемы после коммутации. Для его получения необходимо погасить все источники схемы, заменить индуктивности на Lp, емкости- на 1/ Cp и составить выражение для входного сопротивления цепи относительно точек разрыва в любой ветви схемы и приравнять его к нулю
Пассивная схема после коммутации
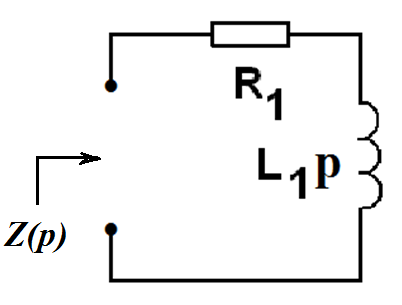
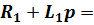 0
0
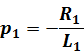
3.Записать общий вид решения для переходного процесса по виду корней характеристического уравнения
Решение складывается из свободной и принужденной составляющих в соответствии с методом Эйлера
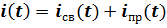
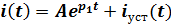
Вид свободной составляющей зависит от вида корней характеристического уравнения. Принужденная составляющая соответствует установившемуся режиму цепи. А-постоянная интегрирования
4.Рассчитать установившийся (принужденный) режим в схеме после коммутации
В установившемся (принужденном) режиме схемы наличие в схеме источника постоянного напряжения обеспечит режим постоянного тока, то есть индуктивность-закоротка.
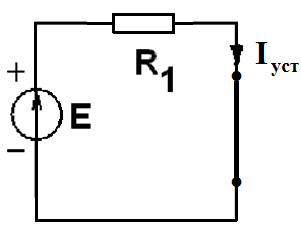
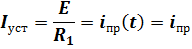
В режиме постоянного тока ток не зависит от времени
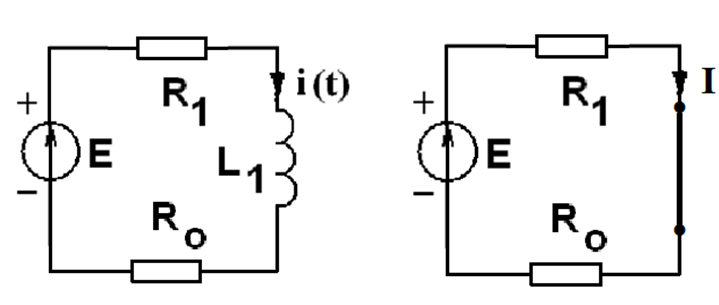
5.Рассчитать независимые начальные условия (ННУ) по схеме до коммутации
До коммутации схема имела вид
В режиме постоянного тока индуктивность - закоротка
I 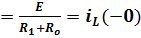
по закону коммутации
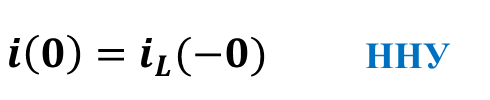
6.Рассчитать зависимые начальные условия (ЗНУ) по схеме после коммутации
Зависимые начальные условия (ЗНУ) находятся по уравнениям Кирхгофа из пункта 1, если эти уравнения записать при t=0
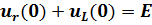
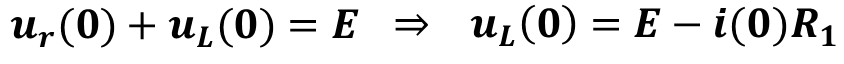
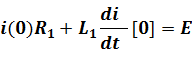
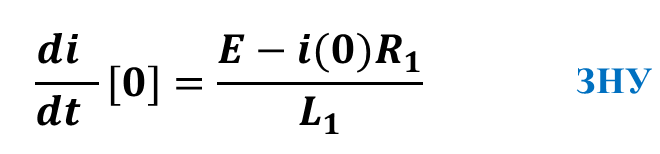
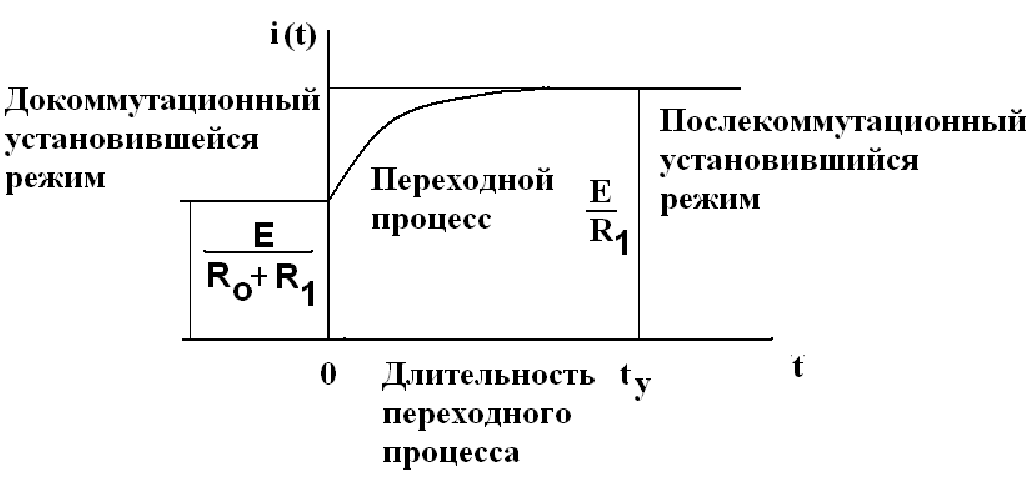
Условное графическое представление переходного процесса в схеме
7.Определить постоянную интегрирования решения переходного процесса
Для определения постоянной интегрирования необходимо записать общий вид решения из п.3 при t=0 и решить полученное уравнение
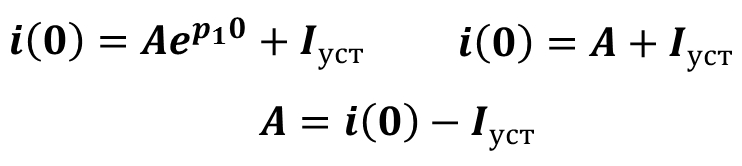
8.Записать окончательное выражение решения и построить его график
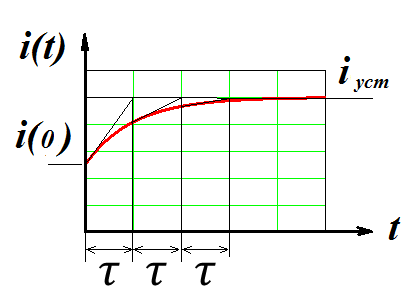
Постоянная времени экспоненты и одновременно постоянная времени цепи первого порядка
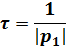
Для цепи первого порядка с индуктивностью
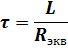
Для цепи первого порядка с емкостью
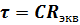
Переходной процесс длится в течении времени
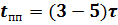
R экв - эквивалентное сопротивление резисторов в пассивной схеме после коммутации относительно зажимов реактивного элемента (индуктивности или емкости) .
Пример 2
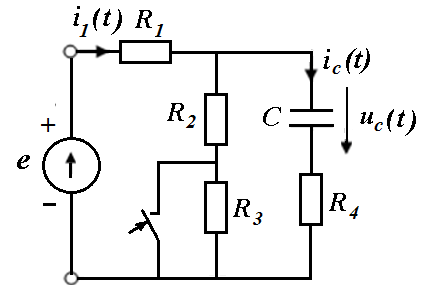
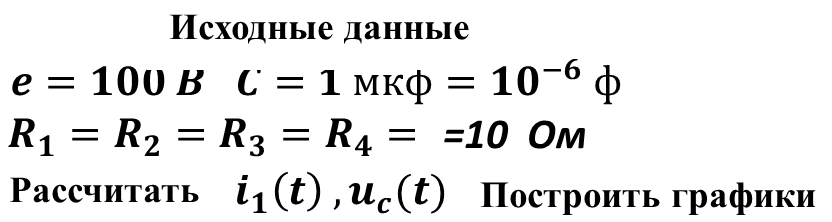
1.Нарисовать схему после коммутации и составить для нее уравнения Кирхгофа
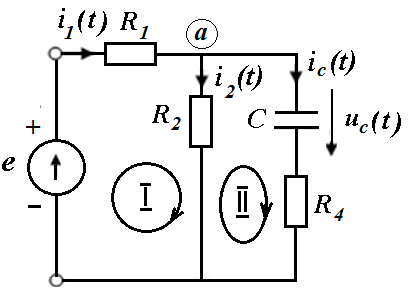
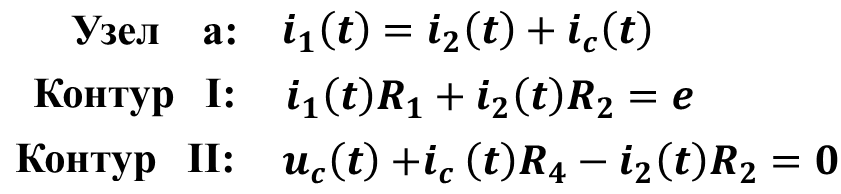
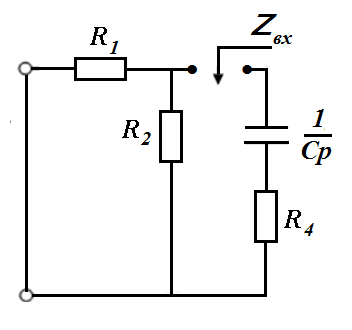
2. Составить выражение для характеристического уравнения, найти его корни
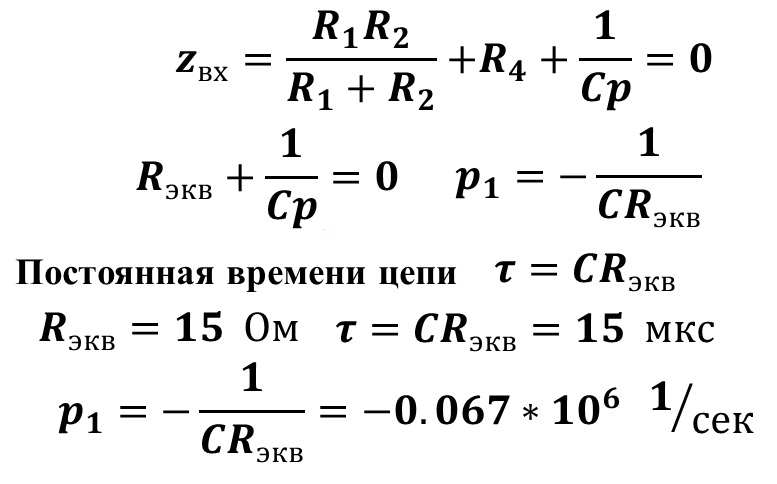
3.Записать общий вид решения для переходного процесса по виду корней характеристического уравнения
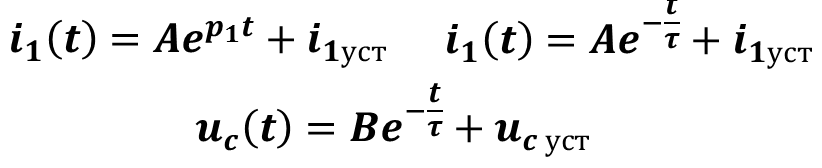
4.Рассчитать установившийся (принужденный) режим в схеме после коммутации
Принужденный режим в схеме после коммутации будет режимом постоянного тока. Емкость –разрыв цепи
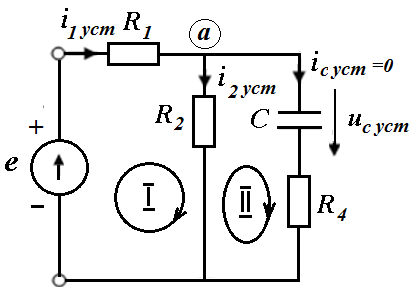
Из уравнений Кирхгофа для установившегося режима следует
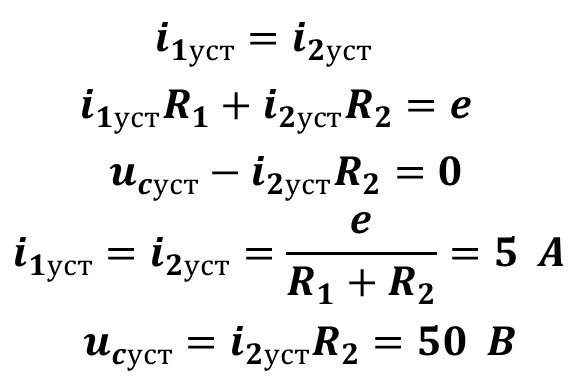
5.Рассчитать независимые начальные условия (ННУ) по схеме до коммутации
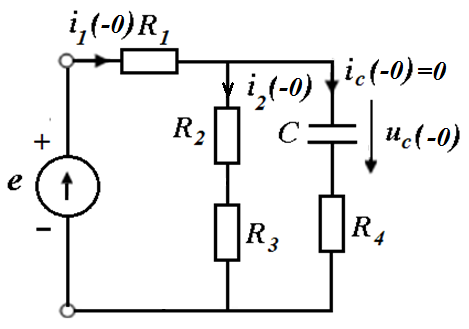
До коммутации в схеме был режим постоянного тока, поэтому 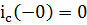 .
.
По законам Кирхгофа
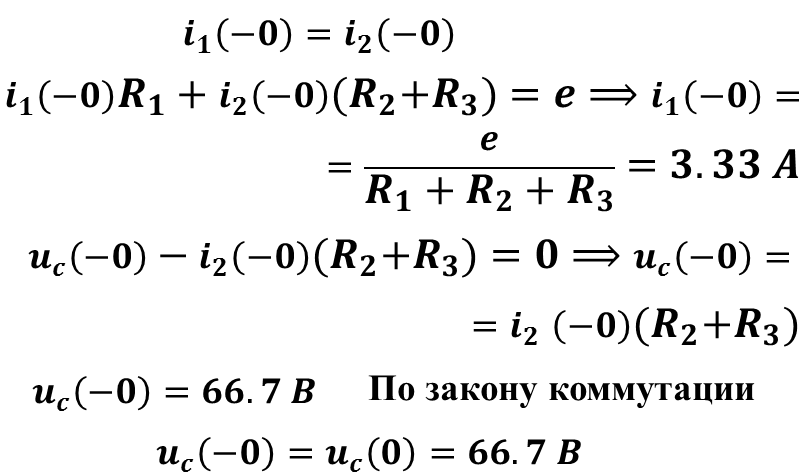
6.Рассчитать зависимые начальные условия (ЗНУ) по схеме после коммутации
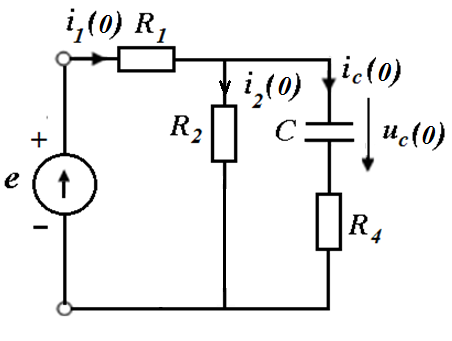
Уравнения Кирхгофа при t=0
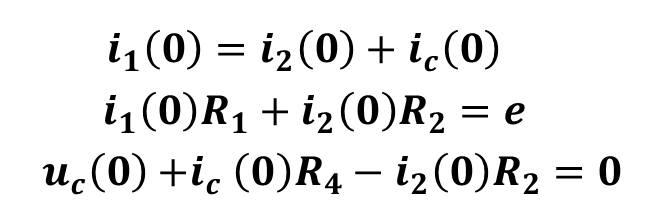
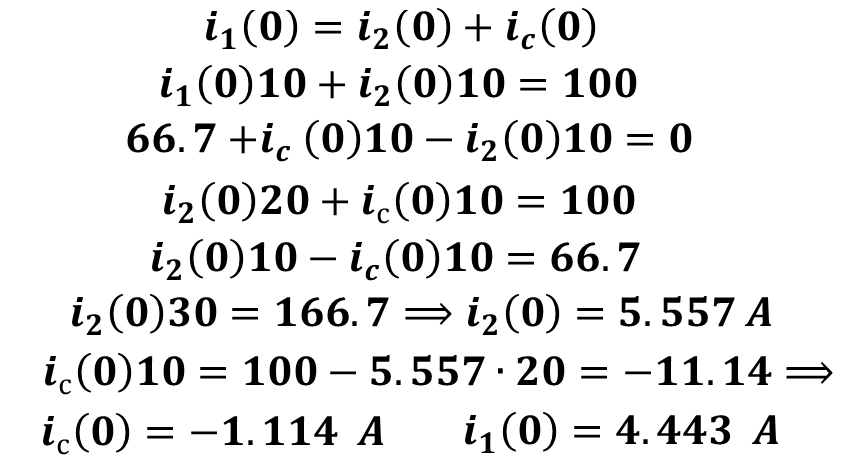
7.Определить постоянные интегрирования решения переходного процесса
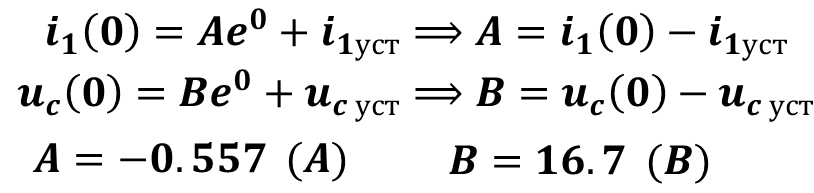
8.Записать окончательное выражение решения и построить его график
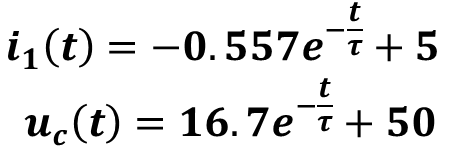
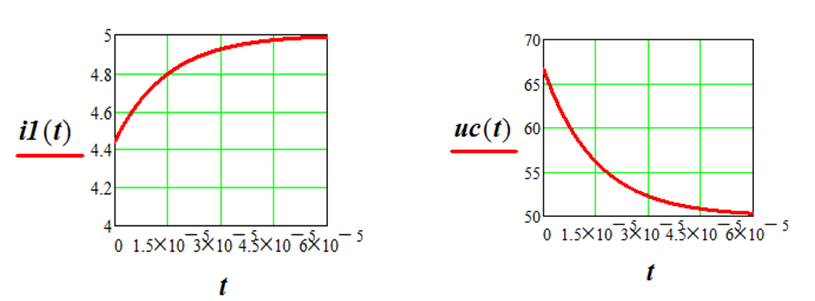
Пример 3
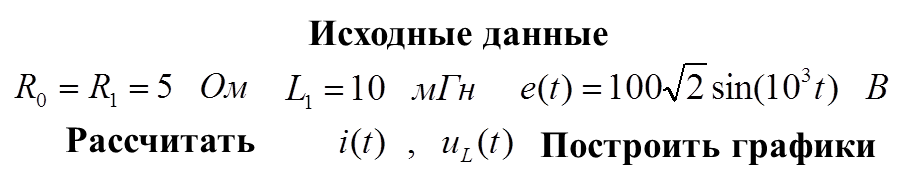
1.Нарисовать схему после коммутации и составить для нее уравнения Кирхгофа
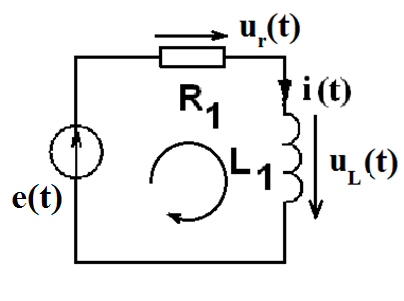
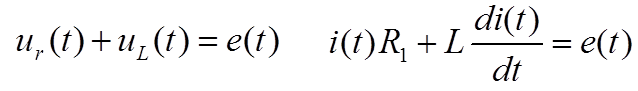
2. Составить выражение для характеристического уравнения, найти его корни
Пассивная схема после коммутации
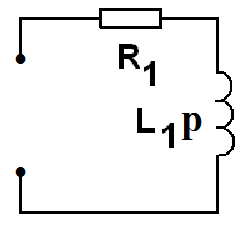
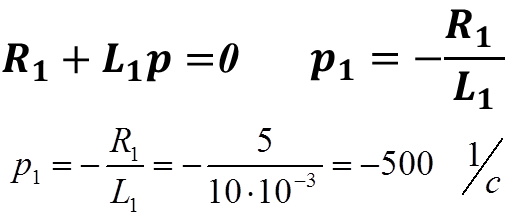
3.Записать общий вид решения для переходного процесса по виду корней характеристического уравнения
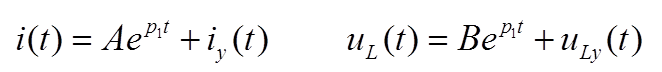
4.Рассчитать установившийся (принужденный) режим в схеме после коммутации
В установившемся (принужденном) режиме схемы наличие в схеме источника синусоидального напряжения обеспечит режим синусоидального тока , то есть расчет следует проводить комплексным методом
Комплексная схема в установившемся режиме имеет следующий вид
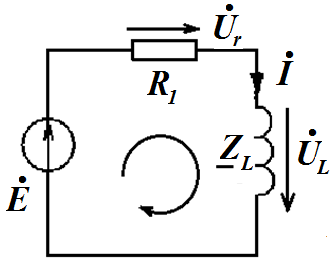
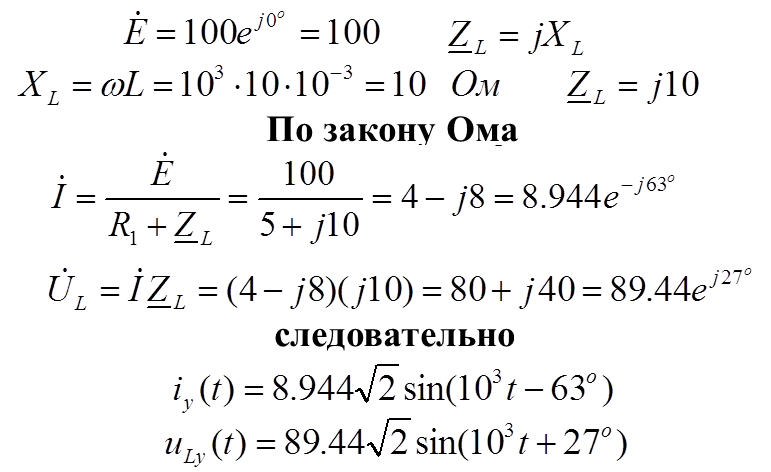
5.Рассчитать независимые начальные условия (ННУ) по схеме до коммутации
Независимым начальным условием для данной схемы является ток в индуктивности
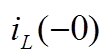
Так как в схеме до коммутации источник напряжения синусоидальный, то расчет также следует провести комплексным методом. Комплексная схема до коммутации имеет вид
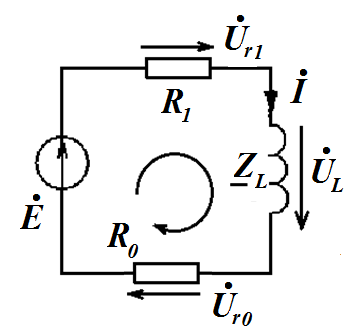

6.Рассчитать зависимые начальные условия (ЗНУ) по схеме после коммутации
Для расчета зависимых начальных условий (ЗНУ) уравнения Кирхгофа из пункта 1 для схемы после коммутации запишем при t=0
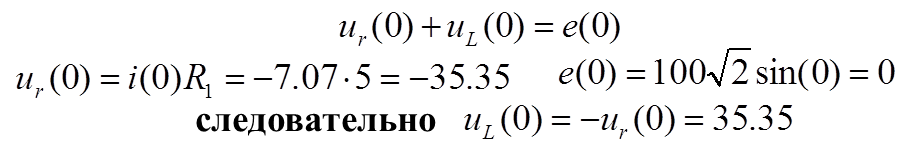
7.Определить постоянные интегрирования решения переходного процесса
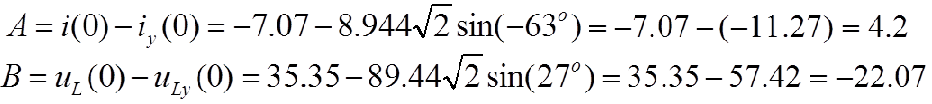
8.Записать окончательное выражение решения и построить графики
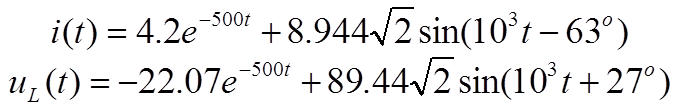
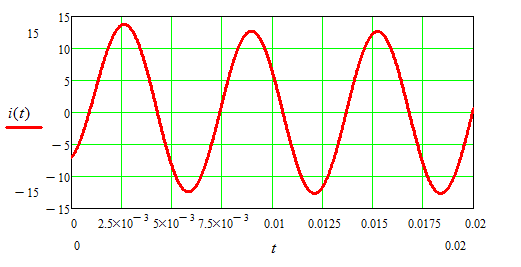
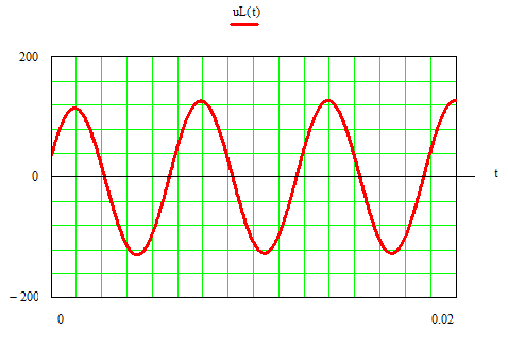
Дата добавления: 2020-03-21; просмотров: 1740;











