Баланс комплексных мощностей

В цепи переменного синусоидального тока сумма комплексных мощностей всех комплексных сопротивлений равна сумме комплексных мощностей источников электрической энергии.

Формализованная запись баланса комплексных мощностей имеет вид

.

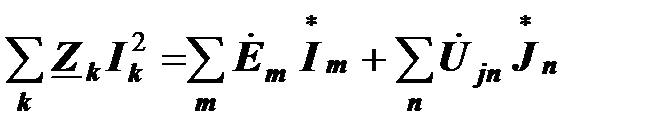Комплексная мощность 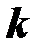- го сопротивления

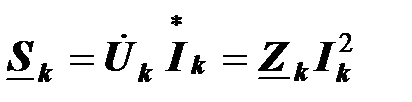
Комплексная мощность 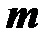- го источника ЭДС

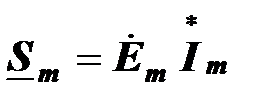
Комплексная мощность - го источника тока

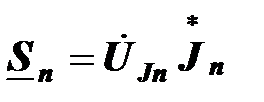
Правила согласования направлений токов и напряжений на элементах цепи иллюстрируется ниже.

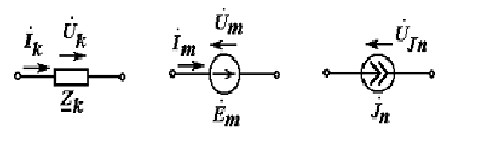
Пример расчета простейших электрических цепей в режиме гармонических колебаний

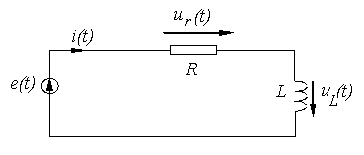
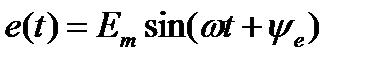
Дано

R , L

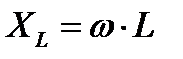
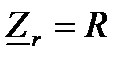
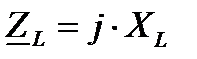
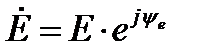решение в буквенных обозначениях

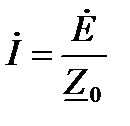
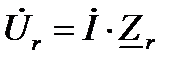
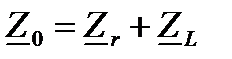
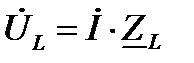
комплексная схема замещения

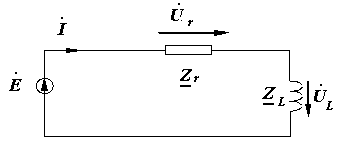
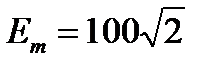
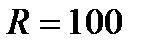Расчет ЭЦ при числовых значениях

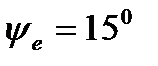
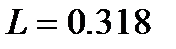В Ом Гн

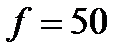Гц

Решение

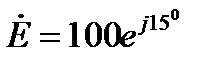
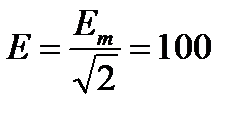
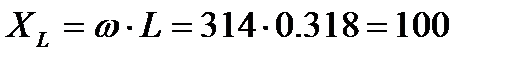
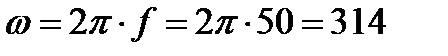1/с

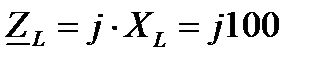Ом

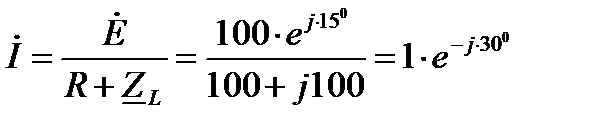
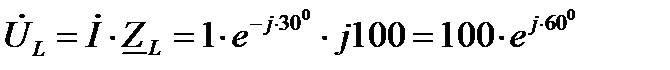
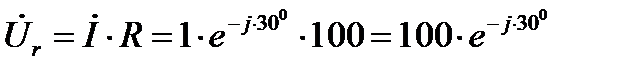
переход от комплексов к синусоидальным функциям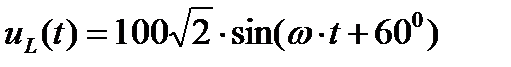

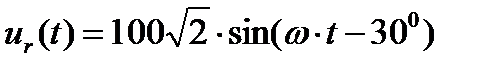
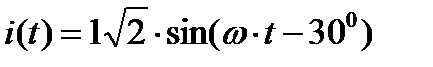
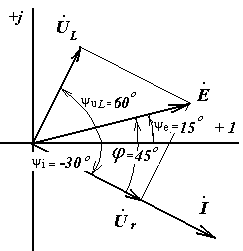
векторная диаграмма тока и напряжений

Резонансные режимы в цепях синусоидального тока

Понятие резонансного режима

Пусть к двухполюснику, содержащему реактивные элементы, приложено синусоидальное напряжение и через него протекает синусоидальный ток. Возможен случай, когда фазы тока и напряжения совпадают. Такой режим работы двухполюсника называется резонансным.

Примечание к определению. Наличие резисторов в двухполюснике возможно, но не обязательно. Двухполюсник должен содержать как катушки, так и конденсаторы. При наличии одних только катушек (или одних конденсаторов) резонансный режим невозможен.

Рассмотрим основные признаки резонансного режима, начиная с условия

.

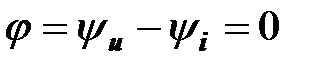Эквивалентное реактивное сопротивление двухполюсника равно нулю

.

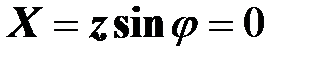Комплексное сопротивление равно эквивалентному активному сопротивле-нию

.

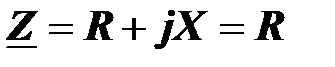Комплексное сопротивление двухполюсника равно его полному сопротивлению

.

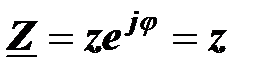Эквивалентная реактивная проводимость равна нулю

.

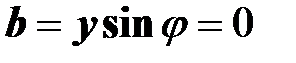Комплексная проводимость равна эквивалентной активной проводимости и равна полной проводимости:

.

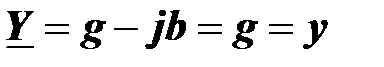Реактивная мощность двухполюсника в резонансном режиме равна нулю

.

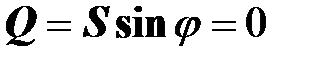Комплексная мощность равна активной мощности и равна полной мощности:

.

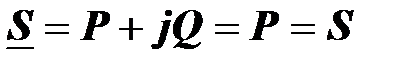Признаки считаются определяющими в том смысле, что они эквивалентны определению резонанса. Некоторые из них чаще всего используются для определения условий возникновения резонансных режимов в конкретных двухполюсниках.

Резонанс напряжений

В резонансном режиме цепи 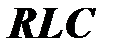(последовательный колебательный контур)

.

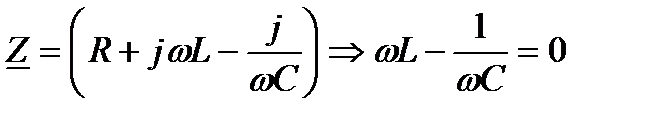Эта цепь может быть настроена в резонанс изменением индуктивности катушки, или емкости конденсатора, или частоты приложенного напряжения. В частности, при постоянных параметрах цепи резонанс наступает при частоте

.

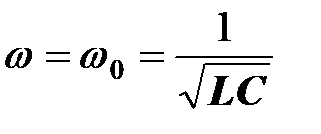Эта частота называется резонансной.

Векторная диаграмма токов и напряжений для резонансного режима получается как частный случай диаграммы, построенной для цепи с последовательным соединением элементов R, L, C. По условию резонанса

, , , .

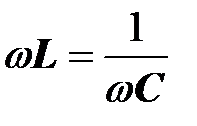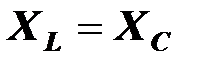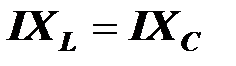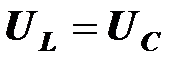Поэтому на диаграмме

, .

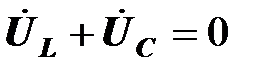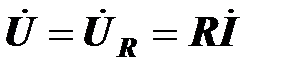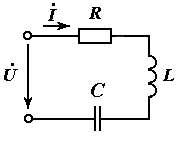
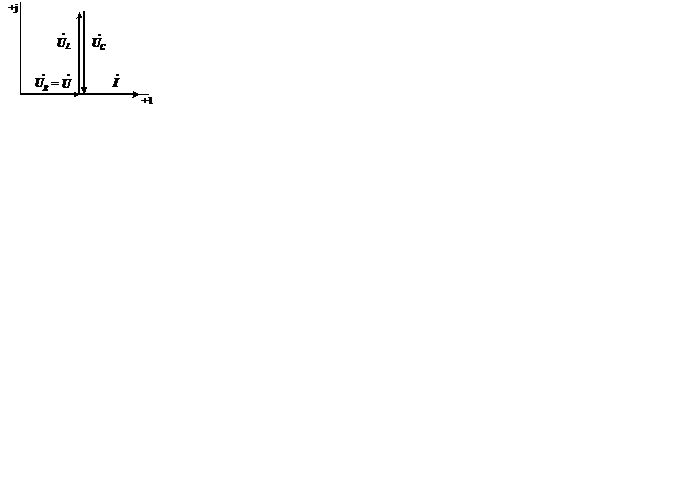
Векторная диаграмма тока и напряжений для резонансного режима

цепи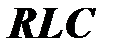

В резонансном режиме в цепи 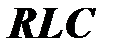напряжения на катушке и конденсаторе равны по величине и отличаются по фазе на 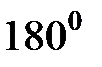(находятся в противофазе). Этот режим называется резонансом напряжений.

В резонансном режиме полное сопротивление цепи минимально и равно активному сопротивлению, соответственно ток принимает максимальное значение

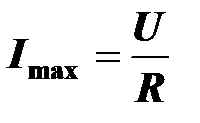
(при условии, что действующее значение входного напряжения поддерживается неизменным).

Если параметры цепи таковы, что в резонансном режиме 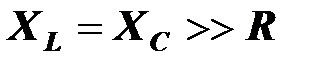, то напряжение на реактивных элементах во много раз больше напряжения на резисторе и напряжения источника. Цепь 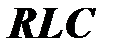в резонансном режиме может быть использована для усиления напряжения ( ).

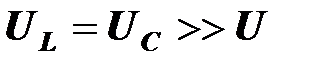Резонанс токов

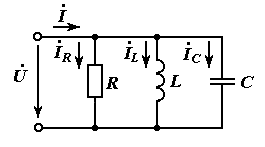
В резонансном режиме в цепи с параллельным соединением резистора, катушки и конденсатора выполняется условие

.

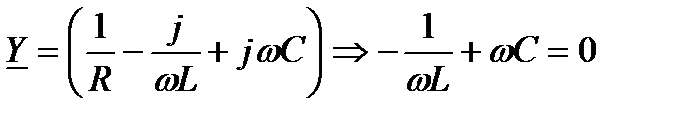Резонанс наступает при частоте источника питания

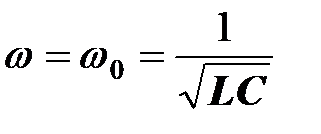
(если параметры реактивных элементов остаются неизменными).

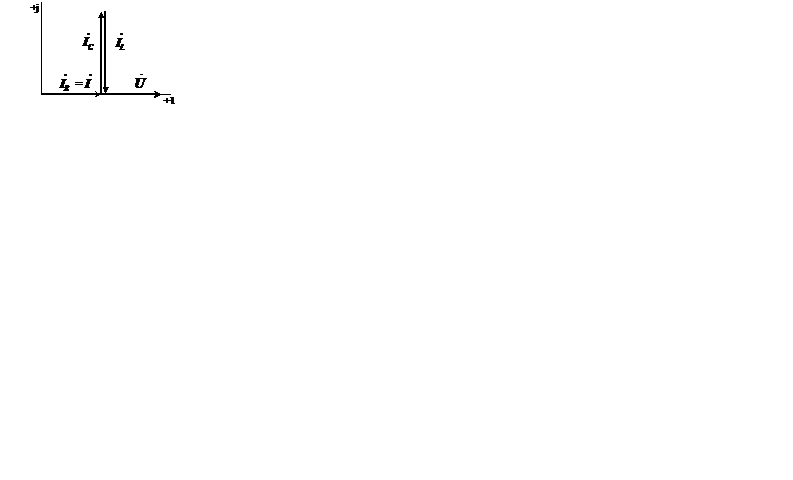
Векторная диаграмма токов и напряжения для цепи

с параллельным соединением элементов , ,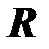

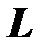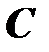
Векторная диаграмма токов и напряжения для резонансного режима является частным случаем диаграммы, построенной для произвольно выбранного режима параллельной цепи.

По условию резонанса

, , , .

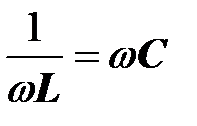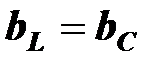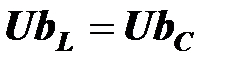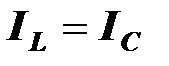Поэтому на диаграмме

, .

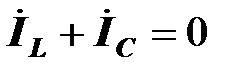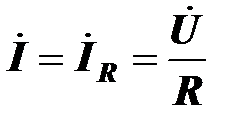В резонансном режиме в цепи с параллельным соединением идеальной катушки и конденсатора их токи равны по величине и отличаются фазами на 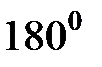. Этот режим называется резонансом токов

В резонансном режиме полная проводимость рассматриваемой цепи минимальна и равна активной проводимости:

, .

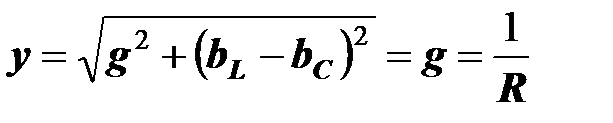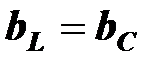Поэтому входной ток в резонансном режиме минимален

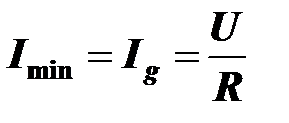
(при условии, что действующее значение входного напряжения поддерживается неизменным, а изменение режима достигается регулированием частоты напряжения, или индуктивности катушки, или емкости конденсатора).

Если рассматриваемая цепь питается от источника синусоидального тока и ее параметры в резонансном режиме таковы, что 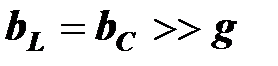, то ток в реактивных элементах во много раз больше тока в резисторе и равного ему тока источника. Можно говорить, что происходит усиление тока (при малом токе источника токи в катушке и конденсаторе велики).

Определение резонансной частоты двухполюсника

Сопротивления реактивных элементов зависят от частоты протекающих в них токов:

, ,

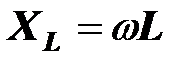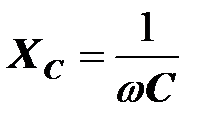поэтому реактивное сопротивление любого двухполюсника, содержащего реактивные элементы, является функцией частоты ( 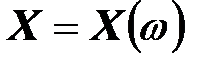). В резонансных режимах

.

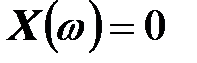Условие резонанса представляет собой уравнение, из которого можно найти резонансные частоты двухполюсника, считая известными параметры его элементов. В общем случае это уравнение является нелинейным, оно может иметь несколько решений или не иметь ни одного решения.

Эквивалентная реактивная проводимость двухполюсника, как и реактивное сопротивление, является функцией частоты источника. Условие резонанса

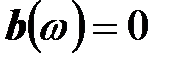
можно использовать для определения резонансных частот.

Резонансные частоты двухполюсника определяются как корни уравнений

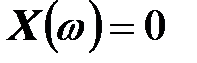или ,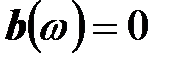

где 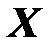- эквивалентное реактивное сопротивление; 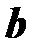- эквивалентная реактивная проводимость двухполюсника.

Пример. Определим резонансную частоту двухполюсника, состоящего из конденсатора и лабораторной катушки, включенных параллельно ). Лабораторная катушка обладает индуктивностью 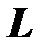, активное сопротивление провода, из которого она изготовлена, равно .

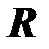Комплексная проводимость двухполюсника равна

.

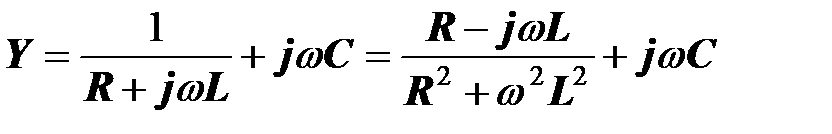Реактивная проводимость двухполюсника равна

.

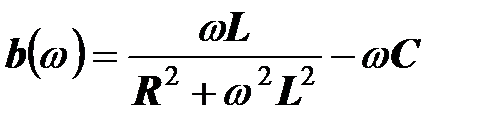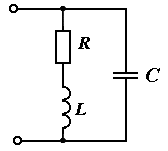
Параллельное соединение лабораторной катушки и конденсатора

Приравняв ее к нулю, получаем условие резонанса

.

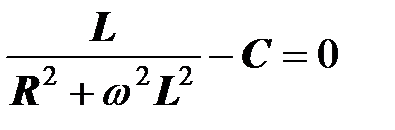Решение 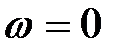невозможно, так как оно соответствует постоянному току, а в цепях постоянного тока резонанса не бывает. Последнее уравнение приводится к вырожденному квадратному уравнению

,

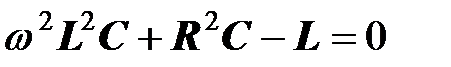его положительный корень равен

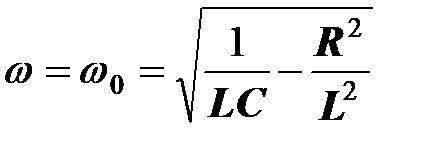(отрицательный корень 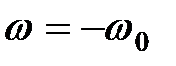не имеет физического смысла).

При параллельном включении идеальной катушки и конденсатора резонансная частота двухполюсника согласно формуле равна

.

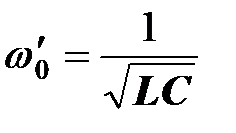В случае, когда используется лабораторная катушка с активным сопротивлением 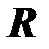, резонансная частота двухполюсника снижается:

.

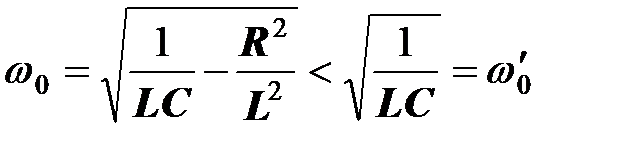При достаточно большом активном сопротивлении катушки под корнем в формуле получается отрицательная величина, и резонанс становится невозможным ни на какой частоте.

Условие передачи максимальной мощности от источника к приемнику

Для упрощения анализа активный двухполюсник представим эквивалентным генератором с комплексной ЭДС 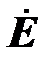и эквивалентным сопротивлением 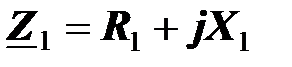, а пассивный двухполюсник эквивалентным комплексным сопротивлением 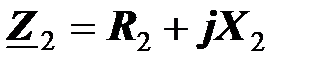. Будем считать, что параметры источника 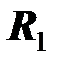и 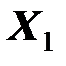фиксированы, а параметры приемника 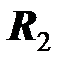и 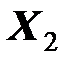можно регулировать.

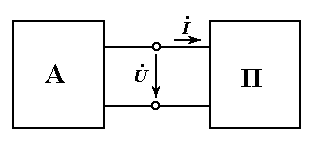
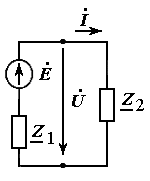
Электрические схемы источника и приемника

Полное сопротивление рассматриваемой цепи равно

.

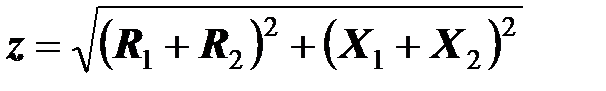Активная мощность приемника равна

.

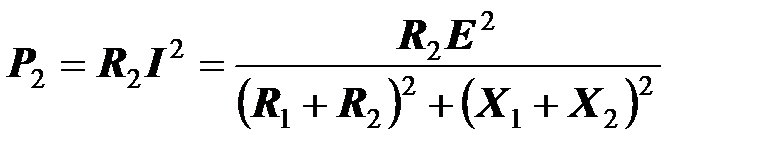При 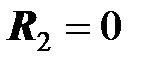, очевидно, 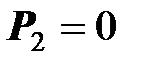. При увеличении активного сопротивления приемника его активная мощность будет увеличиваться и, возможно, достигает максимума. В точке максимума должно выполняться условие

.

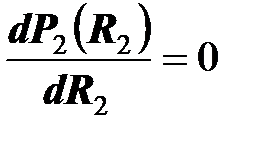Продифференцируем формулу по переменной 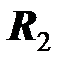и производную приравняем к нулю:

.

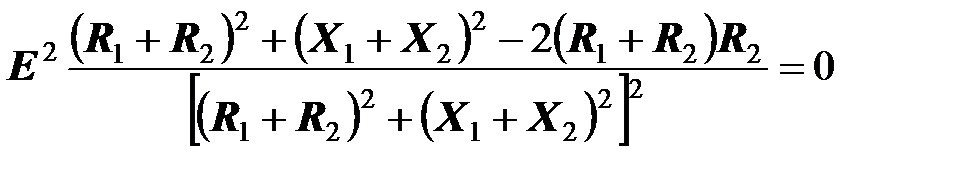После простых алгебраических преобразований получаем, что

.

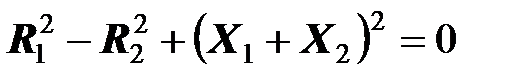Активная мощность приемника максимальна при выполнении двух условий:

1) активные сопротивления источника и приемника равны ( );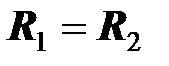

2) эквивалентное реактивное сопротивление цепи равно нулю ( 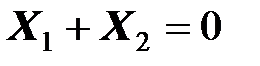), и в цепи установлен резонансный режим.

Оба эти условия можно записать в виде одного комплексного равенства

.

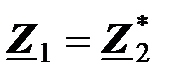Максимальная активная мощность поступает из источника в приемник, если комплексное сопротивление источника равно комплексному сопряженному сопротивлению приемника. Этот режим электрической цепи называется согласованным.

Проблемы коэффициента мощности

В электроэнергетических системах большой мощности повышение коэффициента мощности приемников ( 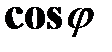) имеет большое экономическое значение.

Пример. Пусть к трансформатору, установленному в заводском цеху, полная мощность которого равна 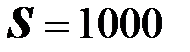кВА, подключаются станки, на каждом из которых смонтированы электродвигатели общей мощностью 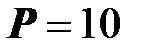кВт.

Если на станках установлены идеально хорошие двигатели с коэффициентом мощности 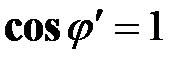, то в цеху можно установить 100 станков:

,

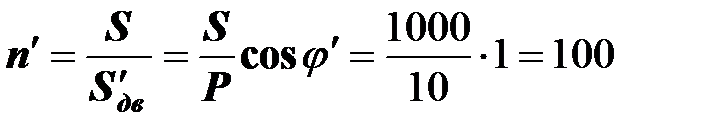где 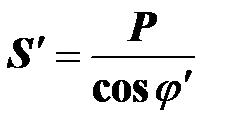- полная мощность хороших электродвигателей на одном станке.

Если на станках установлены необыкновенно плохие двигатели с коэффициентом мощности 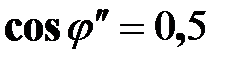, то в цеху можно установить только 50 станков:

,

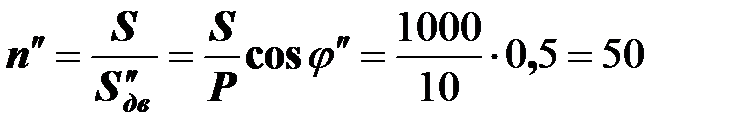где 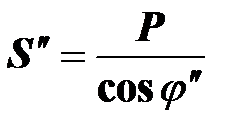- полная мощность плохих электродвигателей из расчета на один станок.

Количество электродвигателей (и станков) на предприятиях ограничивается полной мощностью источников электрической энергии, имеющихся в наличии, и уменьшается при ухудшении коэффициента мощности приемников. Повышение коэффициента мощности приемников электрической энергии позволяет увеличить количество оборудования на предприятиях и получить дополнительную продукцию; прибыль от реализации этой продукции (кроме прочих выгод) окупает расходы на повышение коэффициента мощности.

Повышение коэффициента мощности активно индуктивных приемников с помощью конденсаторов

Любой электродвигатель переменного тока является активно - индуктивным приемником. Он преобразует электрическую энергию в механическую работу, и относительно небольшое количество потребляемой электрической энергии расходуется на нагрев двигателя. Любой электродвигатель представляет собой систему катушек с магнитными сердечниками и не может работать без реактивной мощности, то есть без обмена энергией с источником тока. Простейшая схема замещения электродвигателя содержит резистор, с помощью которого учитывается потребление электрической энергии, и идеальную катушку, которая позволяет учесть требуемую реактивную мощность.

Если включить конденсатор параллельно электродвигателю, то при таком включении конденсатора напряжение на электродвигателе не изменяется (сохраняются условия нормальной работы двигателя) и цепь может быть настроена в резонанс, (то есть коэффициент мощности может быть доведен до единицы). Рассмотрим подробнее вопрос о повышении коэффициента мощности системы электродвигатель плюс конденсатор путем регулирования емкости конденсатора.

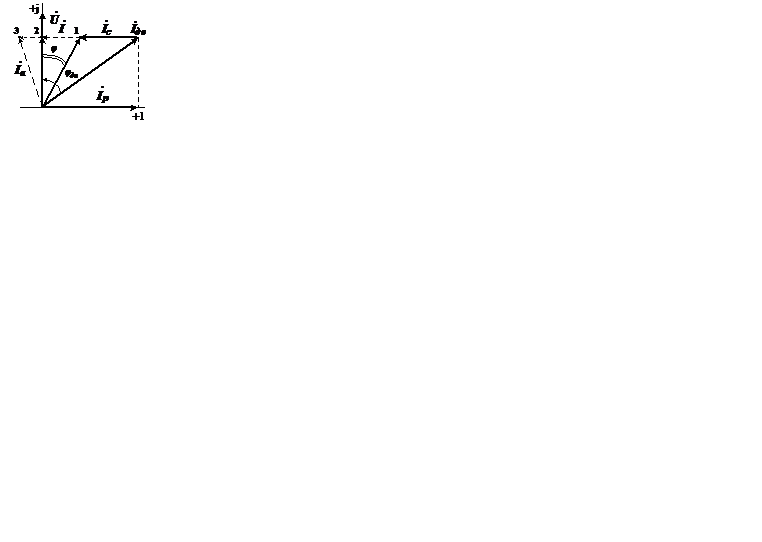
Построим векторную диаграмму токов и напряжений для цепи с параллельным включением катушки и конденсатора.Вектор напряжения, которое одинаково для двигателя и конденсатора, отложим вверх по оси мнимых (чтобы векторная диаграмма оказалась в первом квадранте комплексной плоскости). Ток электродвигателя 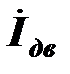имеет активную 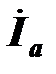и реактивную 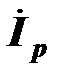составляющие, этот ток отстает от напряжения на угол 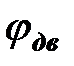. Ток конденсатора 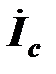опережает напряжение на 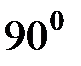. Складывая векторы токов 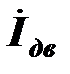и 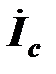по правилу многоугольника, получаем ток источника 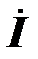(по первому закону Кирхгофа).

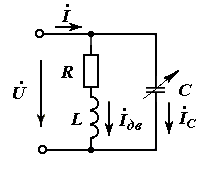
Повышение коэффициента мощности активно - индуктивного

двухполюсника с помощью конденсатора переменной емкости

В случае, если емкость конденсатора относительно невелика, векторы 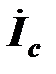и 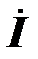заканчиваются в точке 1. Угол 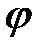между входным током и напряжением на двухполюснике заметно меньше угла 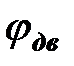для электродвигателя. Коэффициент мощности двухполюсника увеличился по сравнению с коэффициентом мощности двигателя ( , ).

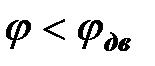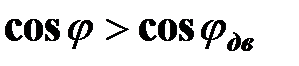Если увеличить емкость конденсатора, ток, протекающий через него, увеличится ( 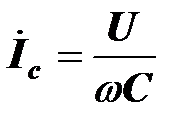). Можно добиться такого увеличения тока 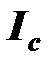, что вектор 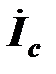и вектор 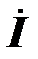будут заканчиваться в точке 2. Это резонансный режим, 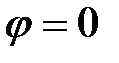. Ток конденсатора равен реактивной составляющей тока двигателя. Ток источника минимален и равен активной составляющей тока двигателя. Источник обеспечивает электродвигатель только той энергией, которая превращается в механическую работу и рассеивается в окружающем пространстве в виде тепла; двигатель обменивается реактивной мощностью с конденсатором. Ток источника уменьшился; к источнику можно подключить дополнительный приемник, не допуская перегрузки источника.

Если после достижения резонанса токов (когда 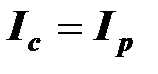) продолжать увеличение емкости конденсатора, то ток конденсатора превысит реактивную составляющую тока двигателя. Векторы 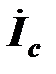и 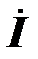на векторной диаграмме будут заканчиваться в точке 3. Легко заметить, что сдвиг фаз между входным током и напряжением на двухполюснике начинает увеличивается, ток источника увеличивается, коэффициент мощности уменьшается. Положительный эффект от включения конденсатора частично утерян.

Для повышения коэффициента мощности активно - индуктивного приемника параллельно ему включают конденсатор такой емкости, чтобы коэффициент мощности составного двухполюсника был близок к единице.