Тема 6. Линейные электрические цепи при несинусоидальных периодических воздействиях
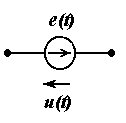
Если в линейной цепи содержатся источники синусоидальных ЭДС разных частот, то ток в любой ветви можно определить как сумму синусоидальных токов разных частот, созданных отдельными источниками. Если в цепи имеется источник периодической ЭДС, то эту ЭДС (разложив ее в тригонометрический ряд Фурье) можно рассматривать как совокупность постоянной и синусоидальных ЭДС кратных частот, включенных последовательно . Каждая из этих ЭДС создает в любой ветви соответствующий ток (постоянный или синусоидальный соответствующей частоты). Все вместе эти ЭДС создают во всех ветвях цепи периодические несинусоидальные токи.
| 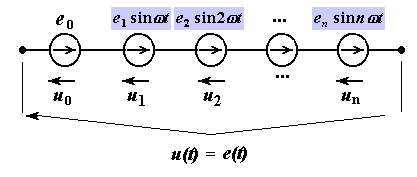
|
Эквивалентность периодической несинусоидальной ЭДС совокупности последовательно включенных постоянной и синусоидальных ЭДС кратных частот
Несинусоидальный ток любой ветви получается суммированием токов, созданных в этой ветви постоянной составляющей ЭДС и синусоидальными составляющими ЭДС кратных частот.
Разложение периодической функции в ряд Фурье
Функция, удовлетворяющая условию
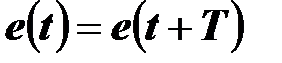 ,
,
где 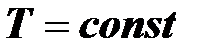 , называется периодической функцией.
, называется периодической функцией.
Наименьшее из всех возможных значений 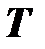 называется периодом функции
называется периодом функции 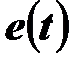
Периодическую функцию (ограниченную по величине), которая имеет конечное число экстремумов и разрывов первого рода на протяжении периода, можно разложить в тригонометрический ряд Фурье
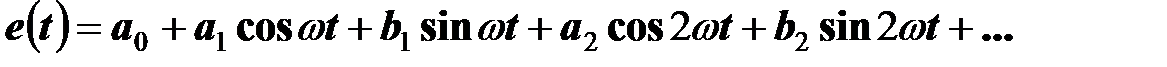 .
.
Коэффициенты этого ряда определяются по известным формулам
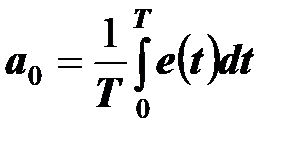 ,
,
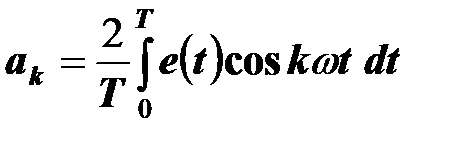 ,
,
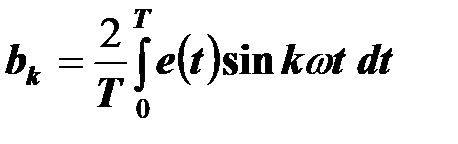 ,
, 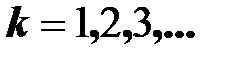 , где
, где 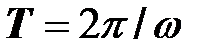 .
.
В технических дисциплинах ряд Фурье используется в следующей форме
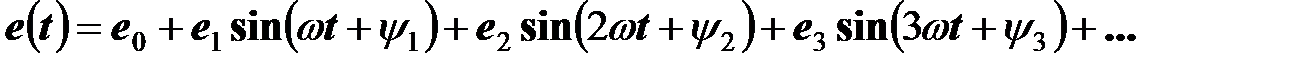 ,
,
где 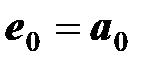 ,
, 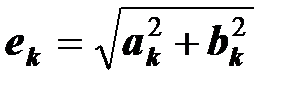 ,
, 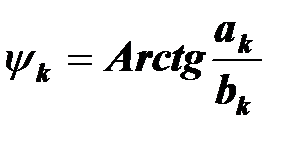 ,
, 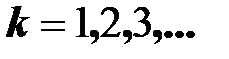 .
.
Здесь 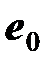 - постоянная составляющая ЭДС
- постоянная составляющая ЭДС 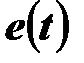 , равная среднему значению функции
, равная среднему значению функции 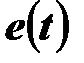 за период; составляющая
за период; составляющая 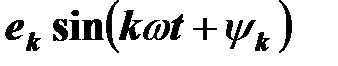 называется
называется 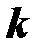 - й гармоникой ЭДС;
- й гармоникой ЭДС; 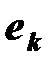 - амплитуда;
- амплитуда; 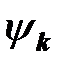 - начальная фаза
- начальная фаза 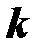 - й гармоники.
- й гармоники.
Первая гармоника ( 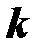 =1) называется также основной гармоникой, ее частота равна частоте периодической несинусоидальной ЭДС. Остальные гармоники называются высшими гармониками.
=1) называется также основной гармоникой, ее частота равна частоте периодической несинусоидальной ЭДС. Остальные гармоники называются высшими гармониками.
Примеры несинусоидальных периодических токов, напряжений, эдс
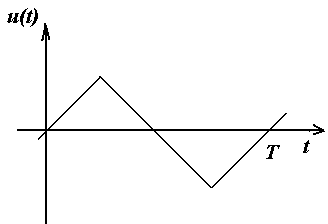
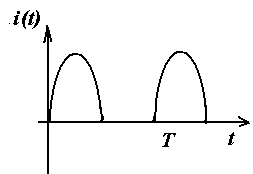
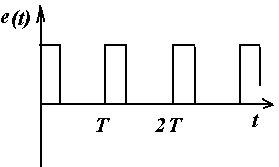
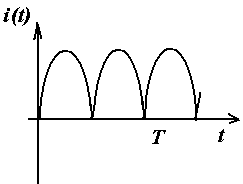
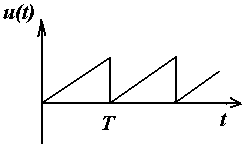

Влияние симметрии периодической функции на гармонический состав ряда Фурье
Симметрия относительно оси ординат (четная симметрия)
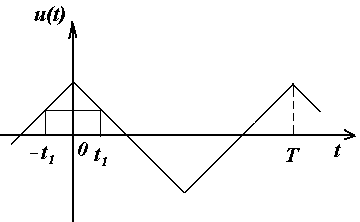
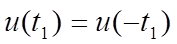
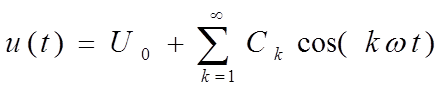
Симметрия относительно оси абсцисс (нечетная симметрия)
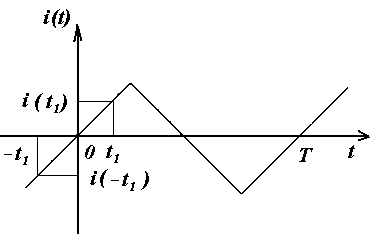
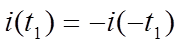
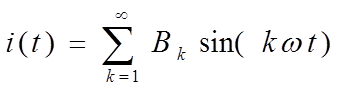
Интегральные величины периодических токов, напряжений, эдс
Среднее значение
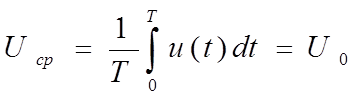
Действующее значение
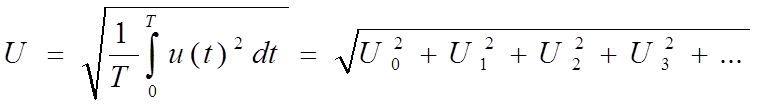
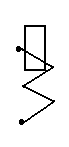
Действующие значения электрических величин измеряются приборами электромагнитной системы, которые имеют неравномерную шкалу; на лицевой панели этих приборов имеется значок, показанный ниже.
Постоянные электрические величины, а также постоянные составляющие переменных электрических величин измеряются приборами магнитоэлектрической системы, которые имеют равномерную шкалу. На лицевой панели этих приборов также имеется специальный значок .
 а)
а)
|
 б)
б)
|
Условные обозначения систем электроизмерительных приборов:
а) электромагнитной, б) магнитоэлектрической
Коэффициенты ,характеризующие несинусоидальность периодической функции
коэффициент амплитуды
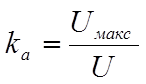
коэффициент формы
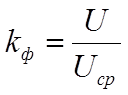
коэффициент искажений
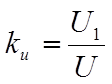
коэффициент гармоник
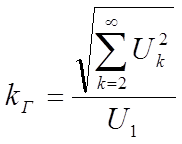
Расчет цепи при несинусоидалных ЭДС
Последовательность расчета
Считаем известными схему электрической цепи и параметры ее элементов (сопротивления резисторов, индуктивности и емкости), а также периодическую несинусоидальную ЭДС 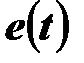 , в частности, ее период
, в частности, ее период 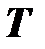
( 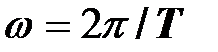 ). Требуется определить токи в ветвях этой цепи.
). Требуется определить токи в ветвях этой цепи.
Порядок расчета входного тока (тока источника ЭДС).
1. Разложить ЭДС в ряд Фурье, или на гармоники.
2. Определить постоянную составляющую входного тока, вызванную постоянной составляющей ЭДС.
3. Определить основную гармонику входного тока, вызванную основной гармоникой ЭДС.
4. Определить необходимое число высших гармоник входного тока, вызванных соответствующими гармониками ЭДС.
5. Определить входной ток как сумму постоянной составляющей, основной гармоники и найденных высших гармоник.
В такой же последовательности вычисляются токи в других ветвях цепи. В таком же порядке можно вычислять все токи электрической цепи совместно, то есть сначала постоянные составляющие всех токов, потом основные гармоники всех токов и т.д.
Расчет каждой гармоники можно выполнить символическим методом. По комплексному току, соответствующему 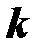 - й гармонике, определяется сама эта гармоника с учетом ее частоты
- й гармонике, определяется сама эта гармоника с учетом ее частоты 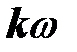 .
.
Предостережение. Нужно помнить, что индуктивные сопротивления катушек и емкостные сопротивления конденсаторов различны для разных гармоник тока (на разных частотах):
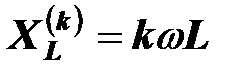 ,
, 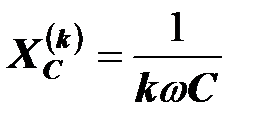 ,
,
где 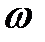 - круговая частота основной гармоники;
- круговая частота основной гармоники; 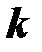 - номер гармоники.
- номер гармоники.
Пример расчета
Пусть к катушке с активным сопротивлением 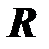 и индуктивностью
и индуктивностью 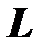 приложено напряжение
приложено напряжение 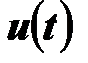 , график которого показан на рисунке. Требуется определить ток в катушке
, график которого показан на рисунке. Требуется определить ток в катушке 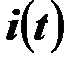 .
.
| 
|
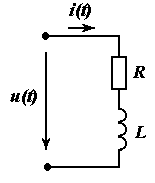
Схема электрической цепи и график приложенного к ней периодического несинусоидального напряжения
1. Ряд Фурье для напряжения 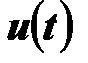 имеет вид (по справочнику).
имеет вид (по справочнику).
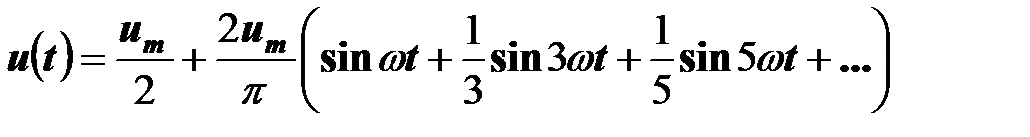 .
.
2. Постоянная составляющая тока создается постоянной составляющей напряжения:
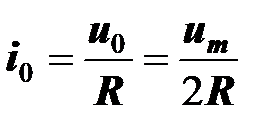 .
.
Индуктивность катушки не влияет на величину постоянного тока.
3. Полное сопротивление катушки основной гармонике тока
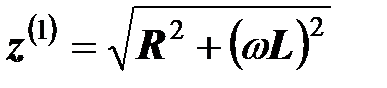 ,
,
основная гармоника тока отстает от основной гармоники напряжения на угол
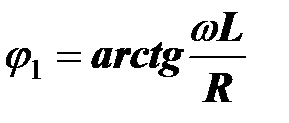 .
.
Основная гармоника тока равна
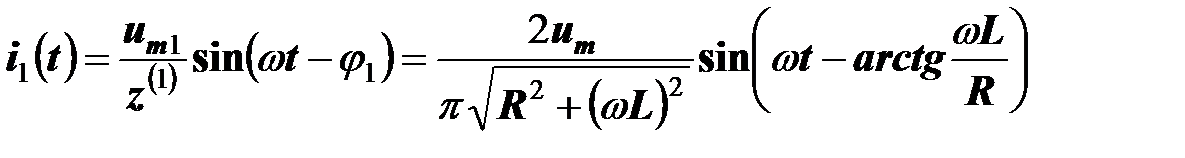 ,
,
где через 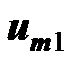 была обозначена амплитуда основной гармоники напряжения, равная
была обозначена амплитуда основной гармоники напряжения, равная 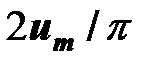 .
.
4. Вторая гармоника тока отсутствует, так как у приложенного напряжения нет второй гармоники.
Полное сопротивление катушки третьей гармонике тока
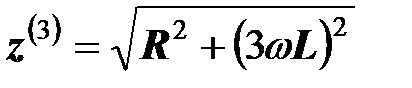 ,
,
разность начальных фаз третьих гармоник напряжения и тока
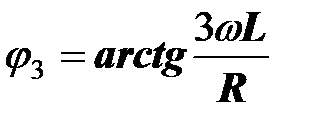 .
.
Третья гармоника тока равна
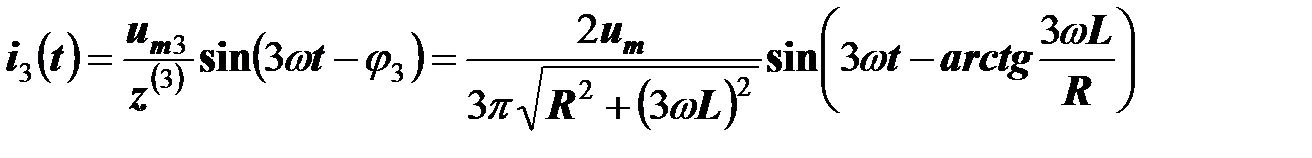 .
.
По аналогии можно записать выражения для пятой и последующих гармоник тока.
5. Если пренебречь пятой и последующими гармониками тока, то искомый ток катушки равен
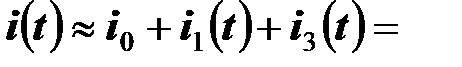
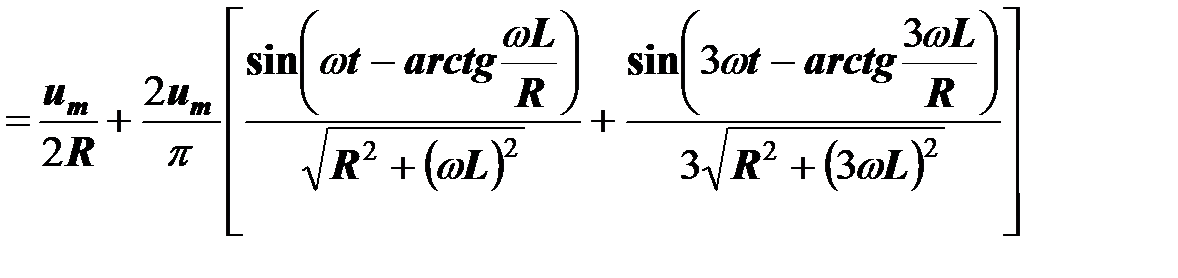 .
.
Гармоники тока суммируются после того, как все они определены как функции времени.
Мощности в цепях несинусоидального тока
Активная мощность двухполюсника по определению равна
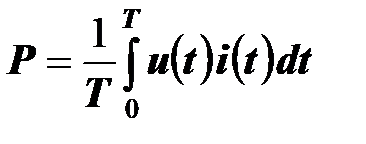 .
.
Если напряжение и ток являются периодическими функциями времени и разложены в ряды Фурье:
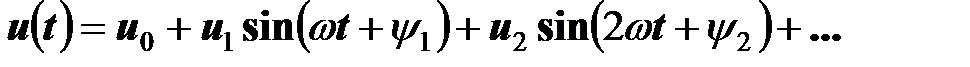 ,
,
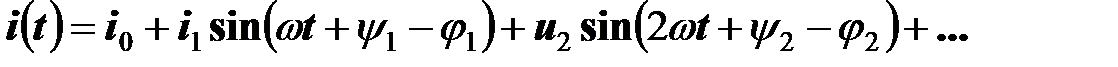 ,
,
где 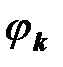 - разность начальных фаз
- разность начальных фаз 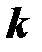 -х гармоник напряжения и тока,
-х гармоник напряжения и тока, 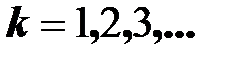 .
.
С учетом результатов интегрирования получаем, что
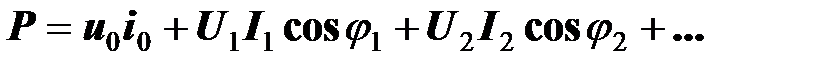 .
.
Активная мощность двухполюсника, по которому протекает периодический несинусоидальный ток, равна сумме активных мощностей, рассчитанных для отдельных гармоник, включая постоянную составляющую тока.
Полную мощность в цепях с несинусоидальными токами можно определять как произведение действующих значений напряжения и тока
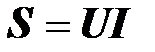 .
.
Реактивную мощность в цепях с несинусоидальными токами, как правило, не определяют, так как при любом ее определении
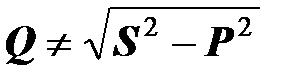 ,
,
т.е. треугольника мощностей не существует.
Коэффициент мощности при несинусоидальном режиме двухполюсника равен
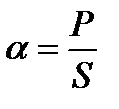
Частотные характеристики
Виды частотных характеристик
При наличии в цепи реактивных элементов ее полное сопротивление, угол сдвига фаз между входным напряжением и током, передаточные проводимости и другие параметры изменяются с изменением частоты приложенного синусоидального напряжения.
Зависимости параметров цепи от частоты называют частотными характеристиками, а зависимости действующих значений (или амплитуд) токов и напряжений от частоты называют резонансными кривыми.
Различают амплитудно-частотные характеристики (АЧХ) и фазо-частотные характеристики (ФЧХ).
Зависимости комплексных сопротивлений и проводимостей от частоты называют амплитудно-фазовыми частотными характеристиками (АФХ), так как они содержат как амплитудно-частотные, так и фазо-частотные характеристики. К амплитудно-фазовым характеристикам относятся передаточные функции четырехполюсников.
Частотные характеристики цепи с последовательным соединением резистора, катушки и конденсатора
Графики амплитудно-частотных характеристик идеальной катушки и конденсатора
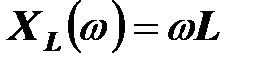 и
и 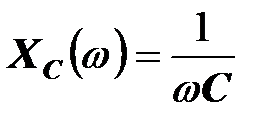
показаны на рис. штриховыми линиями. Сплошной линией нанесен график частотной зависимости реактивного сопротивления цепи, в которой катушка и конденсатор соединены последовательно,
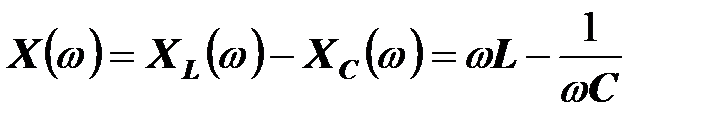 .
.
При частоте 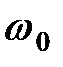 , при которой
, при которой 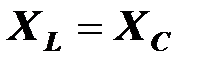 , наблюдается резонанс напряжений (
, наблюдается резонанс напряжений ( 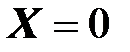 ).
).
При частотах, меньших резонансной, реактивное сопротивление двухполюсника  отрицательно, соответственно аргумент комплексного сопротивления
отрицательно, соответственно аргумент комплексного сопротивления 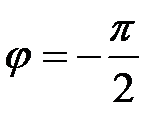 ; при частотах, больших резонансной,
; при частотах, больших резонансной, 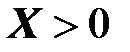 и
и 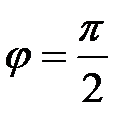 . Фазо-частотная характеристика двухполюсника
. Фазо-частотная характеристика двухполюсника 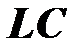 показана на следующем рисунке.
показана на следующем рисунке.

Амплитудно-частотные характеристики идеальной катушки, конденсатора и двухполюсника с их последовательным соединением

Фазо-частотная характеристика двухполюсника с последовательным соединением идеальной катушки и конденсатора
Если последовательно с реактивными элементами 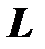 и
и 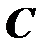 включить резистор, активное сопротивление которого в рассматриваемом диапозоне частот не зависит от частоты, зависимость полного сопротивления цепи от частоты принимает вид
включить резистор, активное сопротивление которого в рассматриваемом диапозоне частот не зависит от частоты, зависимость полного сопротивления цепи от частоты принимает вид

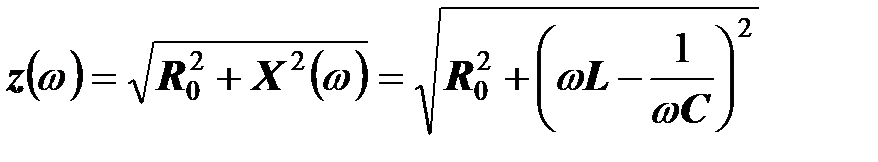 .
.
Ее график показан ниже. При резонансной частоте 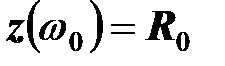 .
.

Амплитудно-частотная характеристика двухполюсника, в котором резистор, катушка и конденсатор соединены последовательно
Фазо-частотная характеристика двухполюсника 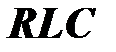 представляется функцией
представляется функцией
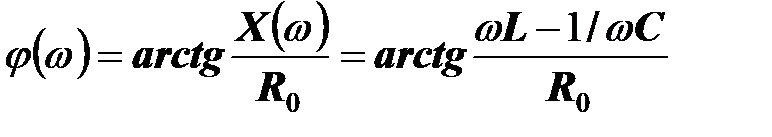 .
.
При резонансной частоте 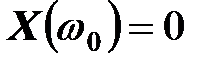 и
и 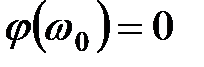 . Когда
. Когда 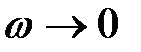 ,
, 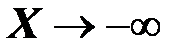 и
и 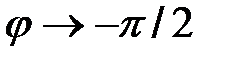 . Если
. Если 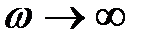 , то
, то 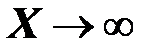 и
и 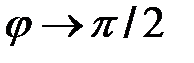 . График функции
. График функции 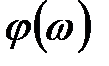 показан ниже.
показан ниже.
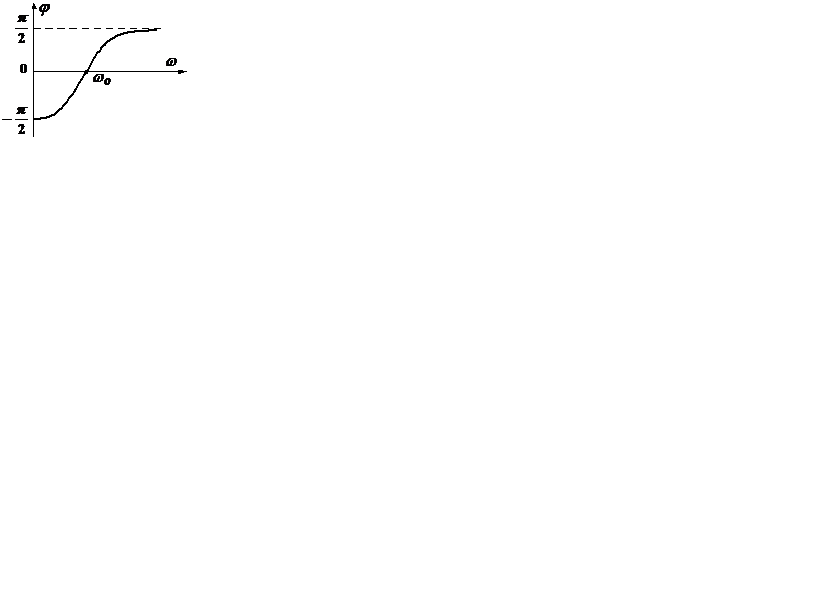
Фазо-частотная характеристика двухполюсника 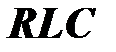
Зависимость действующего значения тока двухполюсника 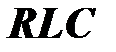 от частоты приложенного напряжения при условии, что действующее значение этого напряжения остается постоянным, имеет вид
от частоты приложенного напряжения при условии, что действующее значение этого напряжения остается постоянным, имеет вид

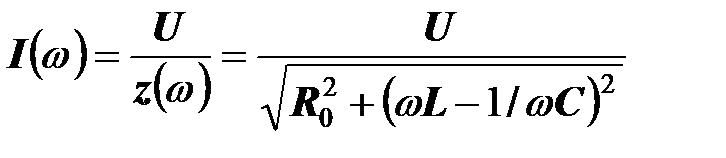 .
.
Величина тока обратно пропорциональна функции 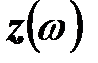 , график функции
, график функции 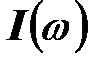 строится в соответствии с графиком
строится в соответствии с графиком 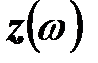 и показан на рисунке. При резонансной частоте
и показан на рисунке. При резонансной частоте 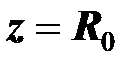 и, следовательно,
и, следовательно, 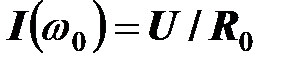 . Если
. Если 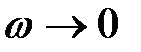 или
или 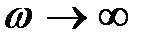 , то
, то 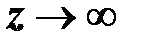 , а
, а 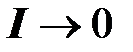 .
.

Резонансная кривая 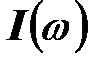 двухполюсника
двухполюсника 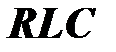
Комплексное сопротивление двухполюсника 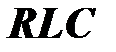 равно
равно
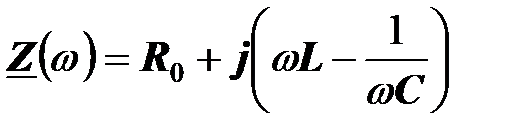 .
.
При изменении частоты изменяется только его мнимая часть. При резонансной частоте 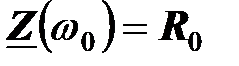 ,
, 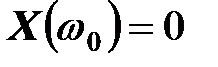 ; при больших частотах
; при больших частотах 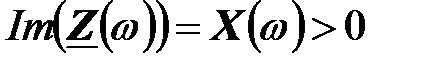 ; при меньших частотах
; при меньших частотах 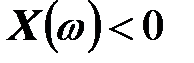 . Соответствующая амплитудно-фазовая характеристика показана на рисунке. Точка, соответствующая нулевому значению частоты, находится на прямой
. Соответствующая амплитудно-фазовая характеристика показана на рисунке. Точка, соответствующая нулевому значению частоты, находится на прямой 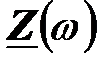 внизу на бесконечности. При увеличении частоты точка перемещается по этой прямой снизу вверх. Некоторому фиксированному значению частоты
внизу на бесконечности. При увеличении частоты точка перемещается по этой прямой снизу вверх. Некоторому фиксированному значению частоты 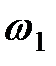 соответствует точка, расстояние которой от начала координат в выбранном масштабе сопротивлений равно полному сопротивлению рассматриваемой цепи при этой частоте. Угол
соответствует точка, расстояние которой от начала координат в выбранном масштабе сопротивлений равно полному сопротивлению рассматриваемой цепи при этой частоте. Угол 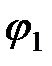 на рисунке равен аргументу комплексного сопротивления цепи при частоте
на рисунке равен аргументу комплексного сопротивления цепи при частоте 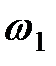 .
.

Амплитудно-фазовая характеристика двухполюсника 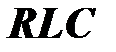
Дата добавления: 2020-03-21; просмотров: 1207;











