Критерии оптимальности для функции нескольких переменных

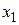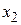Критерии оптимальности необходимы для распознавания решений, а также составляют основу методов поиска решений. Как и для одномерной системы рассмотрим разложение Тейлора для функции нескольких переменных. Для простоты, начнем с двух переменных и . Разложение производим в окрестности точки 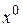. Имеем

.

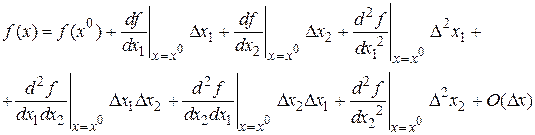Здесь 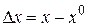- величина изменения 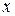, 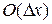- сумма всех членов ряда выше второго порядка по .

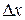То же самое разложение можно записать иначе

,

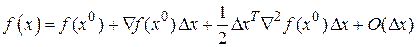где

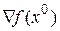- градиент функции 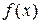, вычисленный в точке ,

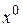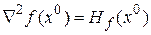симметрическая матрица порядка 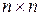вторых частных производных функции 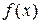, вычисленных в точке .

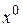Пренебрегая членами высших порядков, определим величину изменения целевой функции, соответствующего произвольному изменению :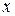

.

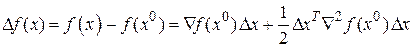Напомним, что по определению, во всех точках окрестности минимума выполняется условие

.

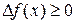Точка 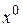будет точкой глобального минимума, если данное неравенство выполняется для всех .

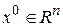Если формула справедлива лишь в некоторой 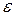-окрестности точки 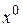, то минимум локальный.

Если 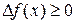, то точка 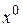есть точка минимума. В случае, если 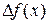принимает положительные, отрицательные и нулевые значения в зависимости от выбора точек из 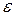-окрестности, точка 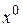представляет собой седловую точку.

Чтобы знак 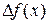не менялся при произвольном варьировании 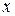, градиент 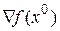должен быть равен нулю, т.е. 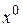должна быть стационарной точкой. Если выполняется условие стационарности, то выражение для приращения функции приобретает вид

.

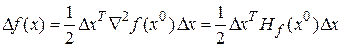Очевидно, что знак 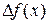определяется квадратичной формой .

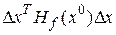Из линейной алгебры известно, что если задана квадратичная форма 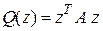, то матрица :

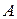· положительно определена, если ;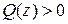

· положительно полуопределена, если ;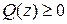

· отрицательно определена, если ;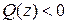

· отрицательно полуопределена, если ;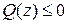

· является неопределенной матрицей, если 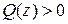для некоторых 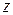и 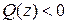для других.

Таким образом, стационарная точка 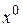есть точка минимума, если 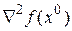- положительно полуопределенная матрица.

Стационарная точка 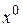есть точка максимума, если 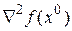- отрицательно полуопределенная матрица.