Метод Коши (Наискорейшего спуска)

Вычисление градиента на каждом шаге, позволяющее все время двигаться в направлении наиболее быстрого убывания целевой функции, может в то же время замедлить вычислительный процесс. Дело в том, что подсчет градиента - обычно гораздо более сложная операция, чем подсчет самой функции, особенно если аналитическое выражение градиента отсутствует. Поэтому часто пользуются модификацией градиентного метода, получившей название метода наискорейшего спуска или метода Коши.

Согласно этому методу после вычисления градиента функции в начальной точке делают в направлении антиградиента не маленький шаг, а движутся до тех пор, пока функция убывает. Достигнув точки минимума на выбранном направлении, снова вычисляют градиент функции и повторяют описанную процедуру. При этом градиент вычисляется гораздо реже, только при смене направлений движения.

Рис. 3.5. Иллюстрация к методу наискорейшего спуска

Хотя траектория ведет к цели не так быстро, как на рис. 3.4, экономия машинного времени за счет более редкого вычисления градиента может быть весьма существенной.

Метод может быть реализован в нескольких вариантах. Простейшим является использование формулы

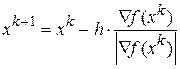
для последовательного движения к экстремуму, пока будет выполняться условие 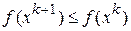. Нарушение данного условия означает прохождение точки минимума и говорит о том, что необходимо изменить направление движения. В достигнутой точке производится новый расчет вектора градиента и процесс повторяется.

Другой вариант состоит в том, что значение шага оптимизации 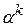вычисляется путем решения задачи минимизации 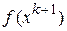вдоль направления с помощью того или иного метода одномерного поиска. Этот вариант реализации алгоритма более сложный, но обычно требует меньшего количества итераций.

Пусть функция 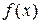дифференцируема по 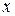и вектор градиента может быть записан аналитически. Тогда поиск минимума функции с использованием процедуры одномерной минимизации включает следующие этапы.

Этап 1. Определение аналитических соотношений для вычисления градиента функции 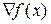, длины вектора градиента 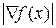и единичного вектора градиента .

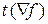Этап 2. Выбор исходной точк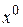и при 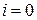(начальных значений аргументов функции).

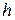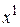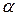Этап 3. Выбор шага изменения координат текущей точки . Осуществляется из условия достижения экстремума функции одного аргумента в соответствии с уравнением

.

Корень этого уравнения, соответствующий минимуму функции , обозначим .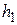

Этап 4. Следующее приближение 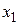вычисляется по формуле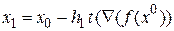

Этап 5. Производится возврат к этапу 3.

В результате формируется последовательность приближений . Вычислительный процесс заканчивается, когда будет достигнута точка 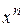, в которой оценка градиента будет равна нулю (коэффициенты функции отклика становятся незначимыми).

Пример. Выполнить шаг наискорейшего спуска для функции вида

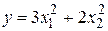
Решение.

Этап 1. Общий вид градиента функции :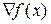

, ,

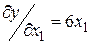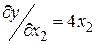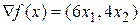
Длина вектора градиента:

Этап 2. Выбор начальной точки, например .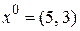

Этап 3. Вычисление координат единичного вектора градиента

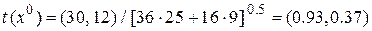
Координаты точки 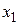при движении по направлению вектора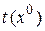

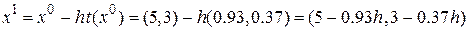
Запишем выражение для функции у в точке 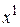как функцию от :

.

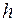Этап 4. Выбор шага 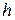изменения координат текущей точки. Найдя производную от 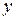по 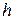в точке 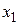и приравняв ее нулю получим 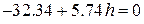. Следовательно, шаг .

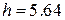Этап 5. Делаем шаг в направлении антиградиента. Координаты точки 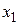после выполнения первого шага наискорейшего спуска по формуле

Аналогично выполняется следующий шаг наискорейшего спуска.

Рассмотренный алгоритм применяют только для нелинейныхфункций. Если функция отклика является линейной, то выбор оптимального значения параметра a невозможен. В этом случае шаг выбирается исходя из эвристических предположений исследователя о виде функции отклика.