Метод эволюционной оптимизации
Идея метода заключается в выборе базовой точки и оценивании значений целевой функции в точках, окружающих базовую точку. Например, при решении задачи с двумя переменными можно воспользоваться квадратным образцом, изображенным на рисунке 3.1.

Рис.3.1. Иллюстрация метода эволюционной оптимизации
Затем, наилучшая из пяти исследованных точек выбирается в качестве следующей базовой точки, вокруг которой строится аналогичный образец. Если ни одна из угловых точек не имеет преимущества перед базовой, размеры образца уменьшаются и поиск продолжается. Такой поиск называется эволюционной оптимизацией.
В задачах большой размерности расчеты проводятся в вершинах гиперкуба. Если число переменных равно 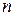 , то поиск по гиперкубическому образцу требует
, то поиск по гиперкубическому образцу требует 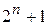 вычислений функции для одного образца. К сожалению, это число растет очень быстро с ростом числа переменных и, несмотря на логическую простоту, эффективность метода для больших
вычислений функции для одного образца. К сожалению, это число растет очень быстро с ростом числа переменных и, несмотря на логическую простоту, эффективность метода для больших 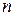 низка.
низка.
Метод поиска по симплексу ( 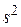 метод)
метод)
Одна из наиболее популярных стратегий прямого поиска экстремума функции нескольких переменных представляет собой поиск по симплесу или 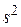 метод. Регулярный симплекс в
метод. Регулярный симплекс в 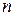 -мерном пространстве представляет собой многогранник, образованный
-мерном пространстве представляет собой многогранник, образованный 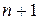 равноотстоящими друг от друга точками-вершинами. Например, в случае двумерного пространства это равнобедренный треугольник (рис. 3.2а), в случае трех переменных – тетраэдр (рис. 3.2б). В алгоритме симплексного метода используется важное свойство симплекса, согласно которому новый симплекс можно построить на любой грани первоначального симплекса путем переноса выбранной вершины на надлежащее расстояние вдоль прямой, проведенной через центр тяжести остальных вершин начального симплекса. Полученная таким образом точка является вершиной нового симплекса, а выбранная вершина начального симплекса исключается.
равноотстоящими друг от друга точками-вершинами. Например, в случае двумерного пространства это равнобедренный треугольник (рис. 3.2а), в случае трех переменных – тетраэдр (рис. 3.2б). В алгоритме симплексного метода используется важное свойство симплекса, согласно которому новый симплекс можно построить на любой грани первоначального симплекса путем переноса выбранной вершины на надлежащее расстояние вдоль прямой, проведенной через центр тяжести остальных вершин начального симплекса. Полученная таким образом точка является вершиной нового симплекса, а выбранная вершина начального симплекса исключается.
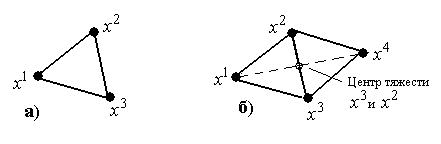
Рис. 3.2 Симплексы в двумерном пространстве
Работа алгоритма начинается с построения начального симплекса и оценивания целевой функции в каждой из его вершин. При этом определяется вершина, которой соответствует максимальное из значений 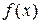 . Затем найденная вершина проецируется через центр тяжести остальных вершин нового симплекса в новую точку, которая используется в качестве вершины нового симплекса. Если функция убывает достаточно плавно, итерации продолжаются пока не будет накрыта точка минимума или не начнется циклическое движение по симплексам. Признаком циклического движения является то, что некоторая вершина не исключается на протяжении более
. Затем найденная вершина проецируется через центр тяжести остальных вершин нового симплекса в новую точку, которая используется в качестве вершины нового симплекса. Если функция убывает достаточно плавно, итерации продолжаются пока не будет накрыта точка минимума или не начнется циклическое движение по симплексам. Признаком циклического движения является то, что некоторая вершина не исключается на протяжении более 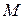 итераций.
итераций.
В таких ситуациях можно воспользоваться следующими правилами.
Правило 1. Если вершина, которой соответствует наибольшее значение целевой функции, построена на предыдущей ирерации, то вместо нее берется вершина, которой соответствует следующее по величине значение целевой функции.
Правило 2.Если некоторая вершина не исключается на протяжении более 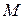 итераций, то размеры симплекса следует уменьшить с помощью коэффициента редукции и построить новый симплекс относительно базовой точки, за которую берется точка достигнутого минимума целевой функции.
итераций, то размеры симплекса следует уменьшить с помощью коэффициента редукции и построить новый симплекс относительно базовой точки, за которую берется точка достигнутого минимума целевой функции.
Поиск завершается, когда или размеры симплекса или разности между значениями функции в вершинах становятся достаточно малыми.
Реализация данного алгоритма основана на вычислениях двух типов:
· построении исходного регулярного симплекса при заданной базовой точке и масштабном множителе;
· расчете координат отраженной точки.
Обе процедуры являются достаточно простыми. При заданных координатах начальной точки и масштабном множителе 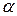 координаты остальных
координаты остальных 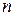 вершин симплекса в
вершин симплекса в 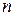 -мерном пространстве вычисляются по формуле
-мерном пространстве вычисляются по формуле
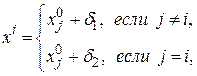
для 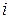 и
и 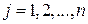 .
.
Приращения 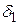 и
и 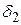 , зависящие только от масштабного множителя
, зависящие только от масштабного множителя 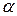 и размерности пространства
и размерности пространства 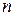 , определяются по формулам
, определяются по формулам
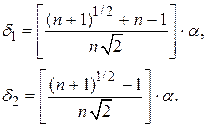
Величина 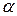 выбирается исследователем исходя из характера решаемой задачи. При
выбирается исследователем исходя из характера решаемой задачи. При 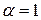 ребра симплекса имеют единичную длину.
ребра симплекса имеют единичную длину.
Вычисления второго типа, связанные с отражение относительно центра тяжести, также не сложны. Пусть 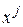 - точка подлежащая отражению. Центр тяжести остальных
- точка подлежащая отражению. Центр тяжести остальных 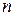 точек расположен в точке
точек расположен в точке
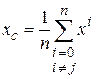 .
.
Все точки прямой, проходящей через 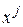 и
и 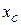 , задаются формулой
, задаются формулой
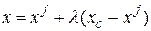 .
.
При 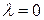 получаем исходную точку, при
получаем исходную точку, при 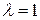 получаем центр тяжести. Симметричное отражение будет при
получаем центр тяжести. Симметричное отражение будет при 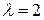 . Таким образом, новая точка может быть получена по формуле
. Таким образом, новая точка может быть получена по формуле
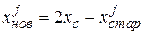 . (3.1)
. (3.1)
Пример. Минимизировать функцию 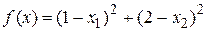 .
.
Прежде всего, требуется задать начальную точку и масштабный множитель. Примем 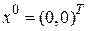 и
и 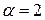 .
.
Вычислим 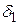 и
и 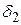 . Имеем
. Имеем
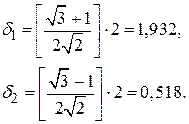
Используя эти два параметра вычислим координаты остальных вершин симплекса:
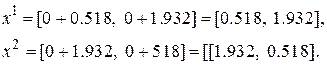
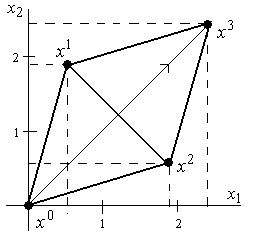
Рис.3.3. Иллюстрация поиска по симплексу
Этим точкам соответствуют значения целевой функции 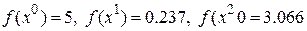 .
.
Так как точкой максимума целевой функции является точка 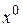 , именно эту точку следует отразить относительно центра тяжести остальных вершин симплекса. Используя формулу (3.1) получаем
, именно эту точку следует отразить относительно центра тяжести остальных вершин симплекса. Используя формулу (3.1) получаем
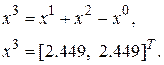
В полученной точке 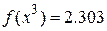 , т.е. наблюдается уменьшение целевой функции. В новом симплексе, образованном точками
, т.е. наблюдается уменьшение целевой функции. В новом симплексе, образованном точками 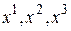 наибольшее значение целевой функции дает точка
наибольшее значение целевой функции дает точка 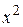 , поэтому именно ее следует отобразить относительно центра тяжести точек
, поэтому именно ее следует отобразить относительно центра тяжести точек 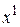 и
и 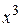 .
.
Преимущества 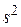 метода:
метода:
· расчеты и логическая структура отличаются относительной простотой. Соответственно программу будет короткой;
· уровень требований к объему памяти ЭВМ невелик, массив имеет размерность 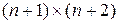 ;
;
· используется сравнительно небольшое число заранее установленных параметров;
· алгоритм эффективен даже при большой ошибке вычисления целевой функции, поскольку используются наибольшие значения в вершинах, а не наименьшие.
Недостатки 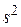 метода:
метода:
· алгоритм работает слишком медленно, т.к. полученная на предыдущих итерациях информация не используется для ускорения счета;
· необходимо масштабировать переменные, чтобы они были сравнимы по величине.
Некоторое улучшение характеристик метода может быть получено, если отказаться от регулярности симплекса, допустив при отражении возможность его растяжения и сжатия.
Градиентные методы
Важность прямых методов несомненна, поскольку в ряде практических инженерных задач информация о значениях целевой функции является единственной надежной информацией, которой располагает исследователь. Однако, применение даже самых эффективных прямых методов часто требует очень большого числа вычислений функции. Это приводит к необходимости изучения методов, основанных на использовании градиента целевой функции. Указанные методы носят итеративный характер, так как компоненты градиента являются, как правило, нелинейными функциями управляемых переменных.
Основная идея всех градиентных методов состоит в том, чтобы двигаться к минимуму в направлении наиболее быстрого убывания функции, которое определяется антиградиентом. Эта идея может реализоваться, например, следующим образом.
Выберем каким-либо способом начальную точку, вычислим в ней градиент рассматриваемой функции и сделаем небольшой шаг в обратном, антиградиентном направлении. В результате мы придем в точку, в которой значение функции будет меньше первоначального. В новой точке повторим процедуру: снова вычислим градиент функции и сделаем шаг в обратном направлении. Продолжая этот процесс, мы будем двигаться в сторону убывания функции.
Наглядной интерпретацией задачи градиентного спуска можно считать положение человека, который хочет максимально быстро спуститься на дно котловины, заросшей лесом, но видит перед собой лишь ограниченный участок местности. В такой ситуации логичным алгоритмом действия является движение в ту сторону, где местность наиболее круто идет вниз, т.е. в сторону антиградиента функции высоты.
Далее везде будем предполагать, что 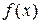 ,
, 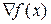 существуют и непрерывны. Предполагается, что компоненты градиента могут быть записаны в аналитическом виде или с достаточно высокой точностью вычислены при помощи численных методов.
существуют и непрерывны. Предполагается, что компоненты градиента могут быть записаны в аналитическом виде или с достаточно высокой точностью вычислены при помощи численных методов.
Замечание. В практических задачах найти значения производных целевых функций вида 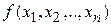 аналитически, как правило, не удается и их вычисляют приближенно:
аналитически, как правило, не удается и их вычисляют приближенно:
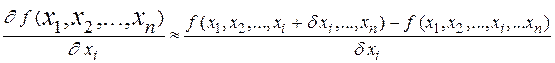 .
.
Выбор величин приращений по координатам 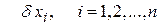 зависит от возможностей используемой ЭВМ и необходимой точности вычислений.
зависит от возможностей используемой ЭВМ и необходимой точности вычислений.
Все градиентные методы поиска минимума основаны на итерационной процедуре, реализуемой в соответствии с формулой
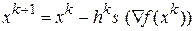 ,
,
где 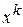 – текущее приближение к решению
– текущее приближение к решению 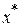 ;
;
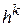 – параметр, регулирующий длину
– параметр, регулирующий длину 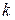 -го шага;
-го шага;
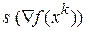 – направление поиска в
– направление поиска в 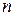 - мерном пространстве управляемых переменных
- мерном пространстве управляемых переменных 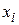 ,
, 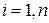 .
.
Способ определения 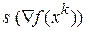 и
и 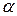 на каждой итерации связан с особенностями применяемого метода.
на каждой итерации связан с особенностями применяемого метода.
Ранее уже отмечалось, что градиент функции 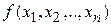 в точке
в точке 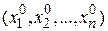 - это вектор
- это вектор
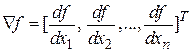 ,
,
проекции которого являются производными по координатам и вычислены для 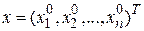 . Длина вектора градиента
. Длина вектора градиента
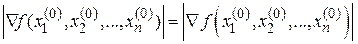 (3.2)
(3.2)
характеризует скорость возрастания функции в этой точке, а направление соответствует направлению быстрейшего возрастания функции. Антиградиент - это вектор такой же длины, направленный в противоположную сторону (рис. 3.3). В точке минимума градиент функции равен нулю.
Единичный вектор градиента определяется как
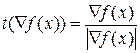 .
.
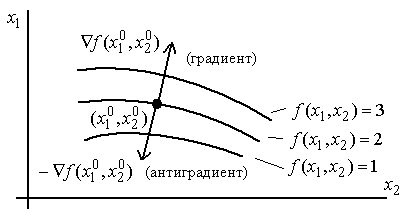
Рис. 3.3. Градиент и антиградиент функции
При поиске минимума каждая следующая точка поиска 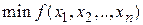 (каждый новый член минимизирующей последовательности) получается в результате перемещения из предыдущей точки по направлению антиградиента целевой функции по формуле
(каждый новый член минимизирующей последовательности) получается в результате перемещения из предыдущей точки по направлению антиградиента целевой функции по формуле
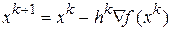 .
.
Если в результате этого перемещения наблюдается увеличение значения целевой функции, то значение рабочего шага поиска уменьшается. Поиск прекращается, когда выполняется необходимое условие 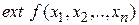 , например, длина вектора градиента становится меньше требуемой точности:
, например, длина вектора градиента становится меньше требуемой точности:
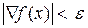 . (3.4)
. (3.4)
Различают методы градиента с переменным шагом и с постоянным шагом (рис. 3.4). При использовании метода градиента с переменным шагом изменение значений 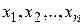 производится согласно выражению
производится согласно выражению
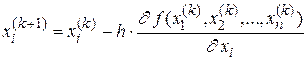 , i=1,2,...,n , k=0,1,2…, (3.5)
, i=1,2,...,n , k=0,1,2…, (3.5)
а останов поиска - при выполнении неравенства (3.4). При возникновении ситуации 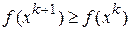 значение параметра h уменьшается, например, делится на число
значение параметра h уменьшается, например, делится на число 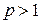 . Характер изменения значений
. Характер изменения значений 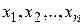 , согласно (3.5), зависит от величины и знака соответствующих частных производных целевой функции.
, согласно (3.5), зависит от величины и знака соответствующих частных производных целевой функции.
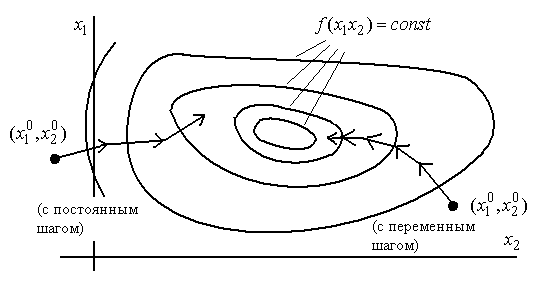
Рис. 3.4. Методы с постоянным и переменным шагом
К недостаткам метода можно отнести то, что, во-первых, на каждом шаге необходимо определять значение градиента. Это может быть не просто, если градиент определяется экспериментально. Во-вторых, по мере приближения к точке 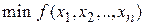 абсолютные величины частных производных уменьшаются, следовательно, и шаг поиска является переменным – уменьшается по мере приближения к искомой точке. Такой характер поиска
абсолютные величины частных производных уменьшаются, следовательно, и шаг поиска является переменным – уменьшается по мере приближения к искомой точке. Такой характер поиска 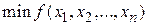 требует иногда весьма значительных затрат времени.
требует иногда весьма значительных затрат времени.
Второй из отмеченных недостатков может быть устранен применением метода градиента с постоянным шагом. Метод позволяет сократить затраты времени, но требует несколько большего объема вычислений при изменении значений аргументов целевой функции. Его основное соотношение:
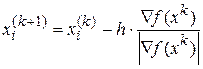 , i=1,2,...,n; k=0,1,2,... . (3.6)
, i=1,2,...,n; k=0,1,2,... . (3.6)
Метод использует вектор градиента единичной длины, который определяет лишь направление градиента, поэтому движение по 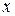 осуществляется с постоянной скоростью, зависящей от величины шага
осуществляется с постоянной скоростью, зависящей от величины шага 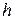 . Если изменение аргументов целевой функции в соответствии с (3.6) приводит к увеличению ее значения, параметр поиска
. Если изменение аргументов целевой функции в соответствии с (3.6) приводит к увеличению ее значения, параметр поиска 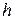 уменьшается. Останов поиска
уменьшается. Останов поиска 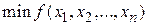 по методу градиента с постоянным шагом осуществляется при выполнении неравенства
по методу градиента с постоянным шагом осуществляется при выполнении неравенства 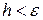 .
.
Дата добавления: 2020-03-17; просмотров: 1509;











