Метод покоординатного спуска.

Желание уменьшить объем вычислительной работы, требуемой для осуществления одной итерации метода наискорейшего спуска, привело к созданию методов покоординатного спуска.

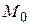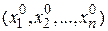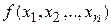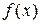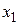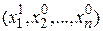Пусть точка с координатами - начальное приближение для функции . Рассмотрим эту функцию при фиксированных значениях всех переменных, кроме первой: . Тогда она превратится в функцию одной переменной . Изменяя эту переменную, будем двигаться от начальной точки x₁=x₁⁰ в сторону убывания функции, пока не дойдем до ее минимума при , после которого она начинает возрастать. Точку с координатами обозначим через , при этом .

Зафиксируем теперь переменные: 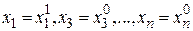и рассмотрим функцию 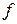как функцию одной переменной 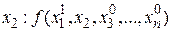. Изменяя 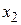, будем опять двигаться от начального значения 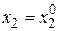в сторону убывания функции, пока не дойдем до минимума при 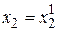. Точку с координатами обозначим через 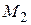, при этом .

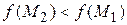Проведем такую же минимизацию целевой функции по переменным 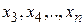. Дойдя до переменной 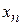, снова вернемся к 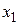и продолжим процесс. Из этой процедуры ясно следует название метода. С ее помощью мы строим последовательность точек 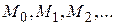, которой соответствует монотонная последовательность значений функции 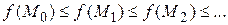Обрывая ее на некотором шаге 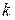, можно приближенно принять значение функции за ее наименьшее значение в рассматриваемой области.

Из изложенного видно, что данный метод сводит задачу поиска наименьшего значения функции нескольких переменных к многократному решению одномерных задач оптимизации. Если целевая функция 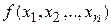задана явной формулой и является дифференцируемой, то мы можем вычислить ее частные производные и использовать их для определения направления убывания функциипо каждой переменной и поиска соответствующих одномерных минимумов. В противном случае, когда явной формулы для целевой функции нет, одномерные задачи следует решать с помощью одномерных методов.

Вычислим частную производную по первой координате и примем:

.

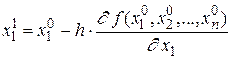Следующая итерация состоит в вычислении точки по формуле:

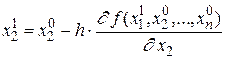
и т. д.

Таким образом, в методах координатного спуска мы спускаемся по ломанной линии, состоящей из отрезков прямых, параллельных координатным осям. Спуск по всем координатам составляет одну «внешнюю» итерацию.

Величина шага выбирается на каждой итерации аналогично тому, как это делается в градиентных методах.

Рис. 3.6. Иллюстрация к методу покоординатного спуска