Структура оптимизационных задач математического программирования

Хотя прикладные оптимизационные задачи математического программирования могут относиться к совершенно разным областям инженерной практики, они имеют общую форму. Все задачи можно классифицировать как задачи минимизации вещественной функции 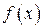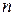-мерного векторного аргумента 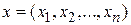, компоненты которого удовлетворяют системе уравнений 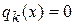, набору неравенств 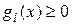, а также ограничены сверху и снизу 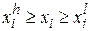. 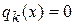В последующем изложении функцию будем называть целевой функцией, уравнения – ограничениями вида равенств, а неравенства 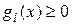– ограничениями вида неравенств. Иногда условия вида 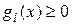называют ограничениями, а условия вида 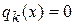– связями.

При этом предполагается, что все функции являются вещественнозначными, а число ограничений конечно.

Система ограничений оптимизационной задачи задает допустимую область 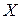переменных 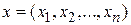, т.е. ту область, в которой может находиться решение задачи.

Задача общего вида:минимизировать при ограничениях

, ,

, ,

, ,

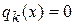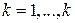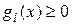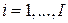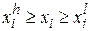называется задачей оптимизации с ограничениями или задачей условной оптимизации.

Задача, в которой нет ограничений, называется задачей без ограничений или задачей безусловной оптимизации.

Следует отметить, что с практической точки зрения задача безусловной оптимизации бессмысленна, так как приводит к нереализуемым результатам. Однако как математическая идеализация она вполне может иметь место. Тем более, что к этой задаче часто искусственно сводятся реальные задачи условной оптимизации.