АРИФМЕТИЧЕСКИЕ ОCНОВЫ ЦИФРОВЫХ УСТРОЙСТВ

2.1 Позиционная система счисления

Под системой счисления понимают способ выражения и обозначения чисел. Общепринятым сейчас является позиционное счисление, в котором значение любой цифры определяется не только принятой конфигурацией ее символа, но и местоположением (позицией), которое она занимает в числе. Изображение чисел в любой позиционной системе счисления с натуральным основанием p(p № 1) базируется на представлении их в виде произведения целочисленной степени основания p на полином от этого основания:

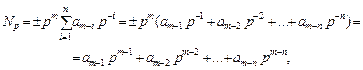
где N_p – натуральное число в системе счисления с основанием p; a_i О {0, 1, 2, …, p – 1} − цифры p − ичной системы счисления; n – количество разрядов, используемых для представления чисел; p^m – характеристика числа, m – показатель, m О{.., – 2, – 1, 0, 1, 2, …}; p^m p^-i = p^m-i – позиционный вес i-го разряда числа, определяемый местом соответствующего символа в изображении числа.

Количество цифр в позиционной системе счисления равно ее основанию. Основанием системы счисления p_i называется количество знаков или символов, используемых для изображения числа в данной позиционной системе счисления. В настоящее время наиболее распространенными являются основания 10, 2, 16, которые иногда обозначаются индексами: D – Decimal, B – Binary, O – Octanary, H – Hexadecimal, соответственно.

Для представления чисел в десятичной системе используются цифры a_i = (0, 1, …, 9), в двоичной – цифры a_i = (0, 1), в шестнадцатеричной – цифры и буквы a_i = (0, 1, …, 8, 9, A, B, C, D, E, F), где прописными латинскими буквами A,…, F обозначены цифры 10, 11, …, 15 десятичной системы. Цифры p_i, необходимые для построения системы счисления, должны удовлетворять неравенству:

0 Ј a_i Ј p – 1.

Если m = const, то это запись числа с фиксированной точкой (запятой). Позиция, в которой запятая фиксируется между разрядами числа, отделяет целую часть от дробной и определяет вес соответствующих разрядов. При m і n числа целые, при m Ј 0 числа дробные и при 0 Ј m Ј n смешанные числа.

В качестве примера запишем десятичное число 8274 в виде целого, смешанного и дробного числа. При m = n = 4 полином этого числа запишется в следующем виде:

10⁴ (8Ч10^–1 + 2Ч10^–2 +7Ч10^–3 + 4Ч10^{– 4}) = 8Ч10³ + 2Ч10² + 7Ч10¹ +4Ч10⁰.

Смешанное число запишем при m = 2 и n = 4:

10² ( 8Ч10^–1 + 2Ч10^–2 +7Ч10^–3 + 4Ч10^{– 4} ) = 8Ч10¹ + 2Ч10⁰ + 7Ч10 ^–1 +

+4Ч10^–2= 82,74.

При m = 0, n = 4 получим дробное число

10⁰ ( 8Ч10^–1 + 2Ч10^–2 +7Ч10^–3 + 4Ч10^{– 4} ) = 8Ч10 ^–1 + 2Ч10^–2 + 7Ч10^–3 +

+4Ч10^{– 4} = 0,8274.

Позиционная система счисления весьма удобна для выполнения различных арифметических операций (сложение, вычитание, умножение, деление), поэтому она является основной в цифровой и вычислительной технике.

Поскольку в цифровой технике основными логическими элементами являются устройства с двумя устойчивыми состояниями, то основной системой счисления является двоичная. В двоичной системе счисления любое число может быть представлено последовательностью двоичных цифр:

где a_i принимает значения 0 или 1.

Эта запись соответствует сумме степеней числа 2, взятых с указанными в них коэффициентами:

Например, двоичное число 10110, 101₂ можно записать как

1Ч2⁴ + 0Ч2³ +1Ч2² +1Ч2¹ + 0Ч2⁰ + 1Ч2^–1 +0Ч2^–2 + 1Ч2^–3,

что соответствует десятичному числу 22,625₁₀.

Для представления служебной информации при подготовке к решению задач на ЭВМ (например, номеров команд, адресов ячеек) применяют вспомогательные системы счисления – восьмеричную и шестнадцатеричную.

Шестнадцатеричная система счисления имеет основание

P = 16 и цифры a_i = 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F. Буквами A, B, C, D, E, F обозначены соответственно десятичные цифры 10, 11, 12, 13, 14, 15. С помощью формул разложения любое шестнадцатеричное число может быть представлено десятичным эквивалентом.

Пример 2.1.1(1E, C)₁₆ = 1Ч16¹ + 14Ч16 ⁰ + 12Ч16^{– 1} = 30,75₁₀.

Запись команд и адресов ячеек памяти в шестнадцатеричной системе счисления еще более короткая, чем в восьмеричной.

2.2 Перевод чисел из одной системы счисления в другую