Сложение и вычитание двоично-десятичных чисел

Операция сложения производится только над модулями двоично-десятичных чисел; знак результата определяется отдельно в результате анализа знаков слагаемых. Сложение модулей десятичных чисел, имеющих одинаковые знаки, производится по следующим правилам:

1. Одно из слагаемых представляется в коде с избытком 6 (таблица 2.3), другое – в коде 8-4-2-1.

2. Сложение двоично-десятичных модулей выполняется по правилам двоичной арифметики.

3. Если при сложении тетрад получается результат больше 10, то автоматически вырабатывается перенос в следующую тетраду. В этом случае результат в данной тетраде получается в естественном двоично-десятичном коде 8-4-2-1 и коррекция для этой тетрады не требуется.

4. Если при сложении в каких-либо тетрадах переносы отсутствуют, то для получения истинного результата из кодов этих тетрад необходимо вычесть избытки 6 (сложить дополнение до 16, т.е. 1010).

Пример 2.4.3

Сложить А = 36₁₀ и B = 58₁₀.

Представим модули чисел А в прямом коде, B – в коде с избытком 6.

Отмеченные « * » тетрады имеют перенос по тетрадам

А = 0011*0110

B_изб = +1011 1110 Код с избытком 6

1111 0100

1010 Коррекция результата

1 1001 0100 Сумма 94₁₀

Перенос теряется

Сложение модулей десятичных чисел, имеющих разные знаки, производится по следующим правилам:

1. Модуль положительного числа представляется в прямом коде 8-4-2-1; модуль отрицательного числа – в дополнительном коде с избытком 6. Для получения дополнения отрицательного числа от модуля надо инвертировать значения разрядов всех его тетрад и к младшему разряду последней (младшей) тетрады прибавить единицу. Дополнительный код от модуля двоично-десятичного числа берется не десятичный, а двоичный, представляющий собой дополнительный код с избытком 6 (тетрады дополняются до 16, а не до 10).

2. Сложение двоично-десятичных модулей выполняется по правилам двоичной арифметики.

3. Если при сложении тетрад получается результат больше 10, то автоматически вырабатывается перенос в следующую тетраду. Если возникает перенос из старшей тетрады, то он теряется, а результату присваивается знак плюс, т.е. результат получается в прямом избыточном коде. Для получения истинного результата необходимо вычесть избытки 6 (сложить дополнение до 16, т.е. 1010₂) в тех тетрадах, где перенос отсутствовал.

4. Если при сложении тетрад (п.2.) перенос из старшей тетрады отсутствует, то результату присваивается знак минус, т.е. результат получается в дополнительном избыточном коде. Для получения истинного результата необходимо инвертировать каждый разряд и к младшему разряду прибавить единицу. После чего провести коррекцию (прибавить дополнение 1010₂) полученного кода в тех тетрадах, у которых был перенос.

Пример 2.4.4 Даны два числа: А = 357₁₀ и B = 196₁₀. Запишем данные числа в прямом, обратном и дополнительном двоично-десятичном кодах:

А_пр = 0011 0101 0111 В_пр = 0001 1001 0110

А_обр = 1100 1010 1000 В_обр = 1110 0110 1001

А_доп = 1100 1010 1001 В_доп = 1110 0110 1010

Пример 2.4.5 Вычтем из числа А = 357₁₀ число B = 196_10, для чего сложим +А_доп и В_доп :

А_пр = 0011 0101 0111

В_доп = 1110 0110 1010

(А+В)_доп = *0001 1100 *0001( «*» имеют перенос)

1010 (проведем коррекцию результата)

(А + В)_пр = 0001 0110 0001

(А – В) = + 1₁₀ 6₁₀ 1₁₀

Пример 2.4.6 Вычтем из числа B = 196₁₀ число А = 357_{10 ,} для чего сложим +В_доп и – А_доп :

В_доп = 0001 1001 0110

А_доп = 1100 1010 1001

(В + А)_доп = 1110 *0011 1111( « * » тетрады имеют перенос)

(А + В)_пр = 0001 1100 0001 (инвертируем каждый разряд и добавим 1₂)

1010 (проведем коррекцию результата)

(В – А) = 0001 0110 0001

(В – А) = – 1₁₀ 6₁₀ 1₁₀

Переполнение разрядной сетки возможно при сложении операндов с одинаковыми знаками. Оно может быть определено по наличию переноса из старшей тетрады.

2.5 Кодирование отрицательных чисел

Для выполнения арифметических операций двоичные числа кодируются специальными машинными кодами: прямыми, дополнительными и обратными, позволяющими заменить операции вычитания операциями суммирования, что упрощает построение арифметическо-логических устройств.

Прямой код. Представление двоичных чисел в прямом коде основано на подаче их в абсолютном виде с соответствующим знаком: плюс – 0 или минус – 1.

Формула для образования прямого двоичного числа имеет вид:

.

Пример 2.5.1

а) N = +0.0101; N_пр = 0.0101

б) N = – 0.0101; N_пр = 1 – (– 0.0101) = 1.0101.

Ноль в прямом коде может выглядеть двояко, т.е. может быть и положительным и отрицательным

а) N = +0.00...00; N_пр = 0.00...00;

б) N = – 0.00...00; N_пр = 1.00...00.

Прямой код используется для хранения чисел в устройствах ввода и вывода информации, а также при выполнении операции умножения.

Обратный код. Формула для образования обратного кода имеет вид:

.

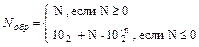Пример 2.5.2

N = – 0.101011₂ ,

N_обр =10₂ – 0.101011 – 0.000001 = 1.010100.

Обратный код положительного числа полностью совпадает с изображением числа в прямом коде. Для получения обратного кода отрицательного числа, нужно в знаковом разряде этого числа поставить единицу, а в числовых разрядах нули заменить единицами, а единицы – нулями.

В обратном коде нуль изображается неоднозначно:

N = + 0.00...00; N_обр = 0.00...00;

N = – 0.00...00; N_обр = 1.11...11.

Дополнительный код. Формула для образования дополнительного кода двоичного числа имеет вид:

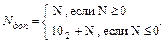
Пример 2.5.3N = 0.1010 = 10₂ + (– 0.1010) = – 1.0101.

Дополнительный код положительного числа полностью совпадает с изображением числа в прямом коде.

Чтобы записать отрицательное число в дополнительном коде, нужно в знаковом разряде этого числа поставить единицу, а во всех числовых разрядах нули заменить единицами, а единицы – нулями и к полученному результату прибавить единицу младшего разряда.

Пример 2.5.4N = – 0.1010, N_обр= 1.0101, N_доп = 1.0110.

В дополнительном коде отрицательный нуль отсутствует.

Модифицированные коды

В отличие от обычных машинных кодов в модифицированных кодах под знак числа отводится два разряда: плюс изображается двумя нулями, а минус – двумя единицами. Это весьма удобно для выявления переполнения разрядной сетки, которое может получиться при сложении чисел с одинаковыми знаками.

Пример 2.5.6

Числа А = + 0.10101 и В = – 0.1010 представить в обратном и дополнительном кодах.

А^M_пр = 00.10101, А^M_обр = 00.10101 , А ^M_доп = 00.10101;

В^M_пр = 11.10101, В^M_обр = 11.01010 , В^M_доп = 11.01011.

Сложение чисел в модифицированном обратном коде. Сложение осуществляется по правилам двоичной арифметики. Отличие состоит лишь в том, что единицу переноса из старшего знакового разряда (если она появляется) необходимо прибавить к младшему разряду суммы (циклический перенос).

Пример 2.5.6Сложить в модифицированном обратном коде двоичные числа А и В при условии: А > 0, В > 0, (А + В) > 0.

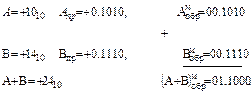
Знак 01 говорит о том, что получен положительный результат, а перенос из старшего разряда в знаковый указывает на то, что произошло переполнение разрядной сетки. Следовательно, истинный результат получен в прямом коде и равен: 0.11000₂ = 24₁₀.

Пример2.5.7 Сложить в модифицированном обратном коде двоичные числа А и В при условии: А > 0,В< 0, (А + В)< 0. Переведем А и В в обратные модифицированные коды и произведем их сложение.

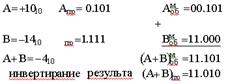
Сочетание двух единиц в знаковых разрядах показывает, что знак суммы отрицательный: (А+В)_пр = 11.0100₂ = – 4₁₀.

Пример 2.5.8Сложить в модифицированном обратном коде двоичные числа А и В при условии: А < 0,В< 0, (А + В)< 0. Переведем А и В в обратные модифицированные коды и произведем их сложение.

Сочетание 10 в знаковых разрядах указывает на то, что результат получен отрицательный (старшая единица), а ноль указывает на то, что произошло переполнение разрядной сетки. Для получения прямого кода проинвертируем биты результата и получим: 1.11000₂ = – 24₁₀.

Сложение чисел в модифицированном дополнительном коде осуществляется по правилам двоичной арифметики. Единица переноса, возникающая в старшем знаковом разряде суммы, отбрасываетсязряд, первый разряд служит для анализа переполнения разрядной сетки.

Пример 2.5.9 Сложить в модифицированном дополнительном коде двоичные числа А и В при условии: А > 0,В< 0, (А + В)< 0. Переведем. Знаковым разрядом числа является второй слева от запятой ра А и В в дополнительные модифицированные коды и произведем их сложение.

Получилось число в дополнительном коде. Переведем его в прямой код, для чего инвертируем каждый разряд числа и к младшему разряду прибавим единицу. Сочетание двух единиц в знаковых разрядах показывает, что знак суммы отрицательный: (А + В)_пр = 11.0100₂ = – 4₁₀.

2.6 Умножение и деление двоичных чисел

Умножение двоичных многоразрядных чисел включает в себя операции определения знака произведения и определение его абсолютной величины. Знаковый разряд произведения может быть получен суммированием цифр знаковых разрядов сомножителей без формирования переноса:

0 + 0 = 0, 1 + 0 = 1,

0 + 1 = 1, 1 + 1 = 0 без формирования переноса.

При несовпадении цифр получается 1, что соответствует знаку произведения двух сомножителей с разными знаками.

Абсолютная величина значения произведения определяется путем перемножения без учета их знаков. Перемножение многоразрядных двоичных чисел производится на основе таблицы двоичного умножения (таблица 3.4). При умножении двух двоичных чисел множимое последовательно умножается на каждую цифру множителя, начиная либо с младшей, либо со старшей. Для учета веса соответствующей цифры множителя он сдвигается либо влево, либо вправо (если умножение производится начиная со старшего разряда множителя), на такое число разрядов, на которое соответствующий разряд множителя сдвинут относительно младшего или старшего разряда. Получающиеся в результате умножения и сдвига частичные произведения после суммирования дают полное произведение. Особенность умножения двоичных чисел состоит в том, что частичное произведение может быть либо сдвинутым на соответствующее число разрядов множимым, если соответствующая цифра множителя равна 1, либо нулем, если соответствующая цифра множителя равна 0.

Пример 2.6.1

Деление двоичных многоразрядных чисел. Деление двоичных многоразрядных чисел включает в себя две операции – определение знака частного и определение его абсолютной величины. Знаковый разряд частного может быть получен, как и знаковый разряд произведения, суммированием цифр знаковых разрядов делимого и делителя без формирования переноса. Абсолютная величина частного определяется делением чисел без учета их знаков. Деление начинается с того, что от делимого слева отделяется группа разрядов, причем количество разрядов в этой группе должно либо равняться количеству разрядов в делителе, либо быть на один разряд больше. Если отделение такой группы возможно, в старшей разряд часто записывается 1, в противном случае в разряд единиц частного записывается нуль. Если выявилось, что частное содержит целую часть, то образуется новая группа разрядов путем вычитания из выделенной группы делителя и приписывания к разности очередной цифры делимого. Если в результате получилось число, превышающее делитель, то в частное записывается 1, в противном случае следующая цифра будет равна 0. В дальнейшем выполняется ряд одинаковых циклов. Если последняя цифра частного была равна 1, то новая группа образуется вычитанием делителя из предыдущей группы и приписыванием очередной цифры делимого. Если последняя цифра частного 0, то для образования новой группы достаточно приписать к предыдущей группе очередную цифру делимого. Последняя цифра целой части частного получается тогда, когда после определения очередной цифры частного 1 или 0 в делимом не останется больше цифр для того, чтобы организовать новую группу. После этого начинается выделение дробных членов частного. Оно отличается от вычисления целых членов только тем, что вместо очередных цифр делимого к предыдущим группам приписываются нули. Рассмотрим пример, в котором делимое больше делителя.

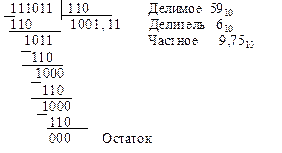
Умножение и деление двоичных чисел, как правило, осуществляют на специализированных арифметических процессорах (сопроцессорах) или программным способом на микропроцессорах.