Метод деления / умножения
Правило перевода целых чисел. Для перевода целого числа Np, представленного в системе счисления с основанием P, в систему счисления с основанием q необходимо данное число делить на основание q (по правилам системы с основанием P) до получения целого остатка, меньшего q. Полученное частное снова необходимо разделить на основание q и т.д., пока последнее частное не станет меньше q. Число Nq в новой системе счисления представится в виде упорядоченной последовательности остатков в порядке, обратном их получению. Причем цифру старшего разряда дает последнее частное.
Пример 2.2.1 Перевести десятичное число 15710 в двоичный код, результат проверить.
| число | делитель остаток |
| 2_____________1 (младший разряд) 2_____________0 2_____________1 2_____________1 2_____________1 2_____________0 15710 = 100111012 2_____________0 2_____________1 (старший разряд) |
Проверка: 100111012 = 1×27 + 0×26 + 0×25 +1×24 + 1×23 + 1×22 + 0×21 + 1×20 = 128 + 16 + 8 + 4 +1 =15710.
Пример 2.2.2 Перевести десятичное число 15710 в восьмеричный код, результаты проверить.
| число | делитель остаток |
| 8_____________5 (младший разряд) 8_____________3 15710 = 2358 8_____________2 (старший разряд) |
Проверка: 2358 = 2×82 + 3×81 + 5×80 = 128 + 24 + 5 = 15710.
Пример 2.2.3 Перевести десятичное число 15710 в шестнадцатеричный код, результат проверить.
| число | делитель остаток | ||
| 16_____13 (младший разряд) 16_____9 (старший разряд) 15710=9D16 | |||
Проверка: 9D16 = 9×161 + 13×160 = 144 + 13 = 15710.
Для облегчения работы с двоичными кодами желательно знать наизусть десятичные значения чисел 2n от n = 0 до n = 14. (Таблица 2.1)
Таблица 2.1
| n | |||||||||||||||
| 2 n | |||||||||||||||
Правило перевода правильной дроби. Перевод правильной дроби Np, представленной в системе счисления с основанием р, в систему с основанием q заключается в последовательном умножении этой дроби на основание q (по правилам системы счисления с основанием р), причем перемножению подвергаются только дробные части. Дробь Nq в системе счисления с основанием q представится в виде упорядоченной последовательности целых частей произведений в порядке их получения, где цифра старшего разряда является первой цифрой первого произведения. Если требуемая точность перевода есть q–k, то число последовательных произведений равно k.
Пример 2.2.4 Перевести десятичную дробь 0,369710 в двоичную систему счисления с точностью до 2–7.
0,3697 0,7394 0,4788 0,9576 0,9152 0,8304 0,6608
´ 2´ 2´ 2 ´ 2´ 2´ 2´ 2 
1,3216 0,7394 1,4788 0,9576 1,9152 1,8304 1,6608
направление чтения
Искомое число в двоичном коде будет равно 0,369710 =
= 0,01011112
Произведем проверку перевода:
0,01011112 = 0×2–1 + 1×2–2 + 0×2–3 + 1×2–4 + 1×2–5 + 1×2–6 + 1×2 –7 =
= 0,3671875.
Пример 2.2.5 Перевести 0,369710 = в восьмеричный код с точностью q–3.
0,3697 0,9576 0,6608
´ 8´ 8´ 8
2,9576 7,6608 5,2864
 направление чтения
направление чтения
Восьмеричный код числа 0,369710 = 0,2758
Проверка перевода:
0,2758 = 2×8-1 + 7×8-2 + 5×8-3 = 0,36914062510.
Пример 2.2.6 Перевести число 0,369710 в шестнадцатеричный код с точностью q–2.
0,3697 0,9152
´ 16´ _ 16
5,9152 14,6432
 направление чтения
направление чтения
Шестнадцатеричный код числа 0,369710 = 0,5E16
Проверка перевода дает:
0,5E16 = 5×16–1 + 14×16–2 = 0,367187510.
При переводе смешанных чисел необходимо отдельно перевести целую и дробную части, а полученные результаты объединить.
Метод вычитания
На первом шаге определяется старший разряд двоичного числа n для переводимого десятичного числа N0 из условия
2 n+1 > N0 ³ 2 n
и в этот разряд вписывается единица. Затем из исходного числа N0 вычитается 2n и находится первая разность:
DN1 = N0 – 2n.
Для этой разности находится следующая максимальная степень числа 2 (в порядке убывания), и производится вычитание, а в соответствующий разряд вписывается единица. Эта процедура продолжается до тех пор, пока десятичное число не станет равным нулю. Разряды, в которых отсутствуют единицы, заполняются нулями.
Пример 2.2.7 Перевести десятичное число 83 в двоичный код.

В итоге имеем 8310 = 10100112.
Перевод дробного десятичного числа выполняется аналогично. Процедура продолжается до получения заданной степени точности.
Пример 2.2.8 Перевести дробное десятичное число 0,5725 в двоичный код методом вычитания (с точностью до семи разрядов).
Подобным образом переводятся десятичные числа в восьмеричный и шестнадцатеричный коды.

Перевод чисел из восьмеричной, шестнадцатеричной системы счисления и обратно. Для перевода числа из восьмеричной системы счисления в двоичную каждую цифру этого числа необходимо записать трехразрядным двоичным числом (триадой). При этом восьмерично-двоичный код совпадает с двоичным.
Пример 2.2.9
(235,275)8 = 010 011 101, 010 111 1018– 2 =10011101, 0101111012
28 38 58, 28 78 58.
Для перевода числа из двоичной системы счисления в восьмеричную необходимо разбить это число вправо и влево от запятой на триады и записать каждую группу цифрой в восьмеричной системе. Крайние неполные триады дополняются нулями.
Пример 2.2.10
10101,01112 = 010 101, 011 1008–2 = 25,348
28 58, 38 48.
Для перевода числа из шестнадцатеричной системы счисления в двоичную необходимо каждую цифру этого числа записать тетрадой, при этом шестнадцатерично-двоичный код совпадает с двоичным, поскольку 16 = 24 .
Пример 2.2.11
9D,5E16 = 1001 1101, 0101 111016–2 = 10011101,01011112
910 1310 , 510 1410.
Для перевода числа из двоичной системы счисления в шестнадцатеричную необходимо разбить это число вправо и влево от запятой на тетрады и каждую тетраду представить шестнадцатеричной цифрой.
Пример 2.2.12
111100,101012 = 0111 1100, 1010 100016–2 = 7C,A816 ,
716 С16 , А16 816.
Основными недостатками двоичной системы счисления являются большая длина разрядной сетки по сравнению с другими системами счисления, необходимость перевода исходных числовых данных из десятичной системы счисления в двоичную, а результатов решения − из двоичной в десятичную.
Двоично-десятичная система счисленияимеет основание d = 10, и каждая цифра (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) изображается в этой системе счисления четырехразрядным двоичным числом, называемым тетрадой. Она используется в ЭВМ не только в качестве вспомогательной системы счисления при вводе и выводе данных, но и в качестве основной при решении задач, когда в ЭВМ вводится и выводится большое количество чисел, а вычислений над ними производится мало. Десятичные числа в двоично-десятичной системе счисления кодируются в прямом нормально-взвешенном коде 8-4-2-1, т.е. каждую цифру десятичного числа необходимо заменить соответствующей тетрадой двоичных чисел.
Для перевода десятичного числа в двоично-десятичный код, десятичный символ следует заменить его двоичным изображением в виде тетрады.
Пример 2.2.13
91,3710 = 1001 0001, 0011 01112–10
910 110, 310 710
Для перевода двоично-десятичного числа в десятичное необходимо исходный код разбить на тетрады вправо и влево от запятой (неполные тетрады дополнить нулями) и заменить полученные тетрады соответствующими десятичными символами.
Пример 2.2.14
11001,001112–10 = 0001 1001, 0101 1000 = 19.5810
110 910 , 510 810
В таблице 2.2 приведены изображения десятичных чисел 0...20 в двоичном, восьмеричном и шестнадцатеричном кодах.
Таблица 2.2
| Десятичное число | Двоичный код | Восьмеричный код | Шестнадца- теричный код |
| A | |||
| B | |||
| C | |||
| D |
Продолжение таблицы 2.2
| E | |||
| F | |||
Код 7421 отличается тем, что любая кодовая комбинация содержит не более двух единиц. В коде 2 из 5 все кодовые комбинации содержат только две единицы из пяти. Это свойство используется для выявления ошибок в кодовых комбинациях (любое отклонение от этого указывает на ошибку). При выполнении арифметических операций широко используются самодополняющиеся коды, инверсия двоичных цифр в которых дает дополнение до 9. Таким свойством обладают код 2-4-2-1, код с избытком 3, код с избытком 6. Например, в коде с избытком 6 цифре 0 соответствует кодовая комбинация 0110, ее инверсия 1001 соответствует цифре 9 (в коде 8-4-2-1), сумма этих чисел 0 и 9 дает 9 (1111) и т.д.(Таблица 2.3).
Таблица 2.3
| Десятичная | Двоичное кодирование десятичной цифры | |||||
| код | код | Код | код 2 из 5 | код с избыт. 6 | код с избыт. 3 | |
2.3 Формы представления чисел в цифровых устройствах
В цифровой технике применяют две формы представления чисел: с фиксированной и плавающей точкой. Эти формы называют соответственно естественной и полулогарифмической.
Представление чисел с фиксированной точкой.
В случае фиксированной точки (запятой) для всех чисел, над которыми выполняются операции в машине, положение точки строго фиксировано – порядок числа P в машине постоянен. Выбор величины P при использовании чисел с фиксированной точкой (запятой), в принципе, может быть произвольным. Положение точки закрепляется в определенном месте относительно разрядов числа и сохраняется неизменным для всех чисел, при этом точка никак не выделяется в коде числа, а только подразумевается. Множество чисел, которые могут быть изображены с помощью n разрядов, представляют собой на числовой оси ряд из 2n равностоящих точек с дискретностью, равной весу младшего разряда, которые заполняют некоторую область между Nmin и Nmax. Любое число между Nmin и Nmax может быть изображено с абсолютной погрешностью, не превышающей половины младшего разряда. Для хранения целых чисел в ячейках памяти предусматривается распределение разрядов (разрядная сетка), показанное в таблице 2.4.
Таблица 2.4
| N – 1 | N – 2 | номера разрядов | |||
| значения разрядов |
 |
знаковый разряды модуля числа
Для всех представляемых чисел их знаки плюс или минус, как правило, обозначают цифрами 0 и 1 соответственно и располагают перед старшим разрядом кода числа (таблица 2.5).
Каждый разряд двоичного числа называют битом. Восьмибитовая единица получила название байт.
Таблица 2.5
| номера разрядов | ||||||||
| значения разрядов |
 |
знаковый разряды модуля числа
Если точка фиксирована после младшего разряда, то могут быть представлены только целые числа. Диапазон представления целых без знаковых чисел:
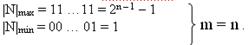
Если количество значащих разрядов модуля числа превышает n–1, происходит потеря старших разрядов модуля. Это явление называется переполнением разрядной сетки и приводит к ошибке в представлении числа. Учет знака приводит к уменьшению диапазона представляемых чисел.
При представлении дробных чисел запятая фиксируется перед старшим разрядом. Диапазон представления дробных чисел:
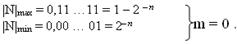
Если представляемое число меньше Nmin, происходит обнуление разрядной сетки.
При представлении смешанных чисел запятая фиксируется (подразумевается) между целой и дробной частью:

 целая часть дробная часть
целая часть дробная часть
| 2 n – 1 | 2n – 2 | 20 | 2–1 | 2–n | веса разрядов | |||||
| значения разрядов | ||||||||||
знаковый разряд
Работа вычислительных устройств с фиксированной точкой используется в основном для управления технологическими процессами и обработки информации в реальном масштабе времени. При выполнении операций с фиксированной точкой основным операндом в ЭВМ является 32-разрядное, в микро- и мини-ЭВМ – 16-разрядное, а в микропроцессорах – 8-разрядное слово (байт). В упакованном формате в одном байте размещаются две десятичные цифры.
Основное достоинство представления чисел с фиксированной запятой (точкой) заключается в том, что имеется возможность построить несложные арифметические устройства с высоким быстродействием.
Дата добавления: 2020-03-17; просмотров: 984;











