Основные положения алгебры логики
Математический аппарат, описывающий действия дискретных устройств, базируется на алгебре логики, автором которой считается английский математик Дж. Буль (1815–1864 г.). В практических целях первым применил его американский ученый К. Шеннон в 1938 г. при исследовании электрических цепей с контактными выключателями.Булева алгебра оперирует двоичными переменными, которые условно обозначают, как 0 и 1. В ее основе лежит понятие переключательной или булевой функции вида f (x1, x2 … xn) относительно аргументов x1, x2 … xn , которая также может принимать лишь два значения – 0 и 1. Логическая функция может быть задана словесно, алгебраическим выражением, и таблицей, которая называется таблицей истинности. Аналитический способ предусматривает запись функции в форме логического выражения, показывающего, какие логические операции над аргументами функции должны выполняться, и в какой последовательности. Сложные функции от многих аргументов могут быть представлены в форме функций от функций, последние из которых выражаются через меньшее число аргументов. При табличном задании функции, в строках таблицы записываются возможные двоичные значения аргументов x1, x2 … xn и указываются значения функции f (x1, x2 … xn), которые она принимает (0 или 1) на данном наборе. При числе аргументов n максимальное число строк в таблице 2 n. В алгебре логики имеются три простейшие логические операции: отрицание (инверсия, операция НЕ), логическое сложение (дизъюнкция, операция ИЛИ), логическое умножение (конъюнкция, операция И).Операция отрицания выполняется над одним аргументом или функцией и обозначается чертой над обозначением аргумента или функции: 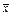 (не
(не  ). Таким образом, инверсия единицы равна нулю, инверсия нуля – единице, а двойная инверсия не изменяет значения переменной:
). Таким образом, инверсия единицы равна нулю, инверсия нуля – единице, а двойная инверсия не изменяет значения переменной:
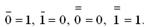
Функциональное обозначение инвертора приведено на рисунке 3.1, а. Дизъюнкция переменных x1 и x2 равна логической 1, если x1 или x2 равны логической единице (таблица 3.1), откуда и возникло название логической операции логическое ИЛИ. Обозначают дизъюнкцию + или V (от латинского Vel – или): y = x1 + x2 либо y = x1  x2. Второй способ предпочтителен, так как позволяет отличить логическое сложение от арифметического. Для двух переменных 0 Ú 0 = 0; 0 Ú 1 = 1; 1 Ú 0 = 1; 1 Ú 1 = 1, т.е. равенство хотя бы одного аргумента логической единице определяет единичное значение всей функции. На функциональных схемах дизъюнктор обозначается цифрой 1 в правом верхнем углу (рисунок 3.1, б).
x2. Второй способ предпочтителен, так как позволяет отличить логическое сложение от арифметического. Для двух переменных 0 Ú 0 = 0; 0 Ú 1 = 1; 1 Ú 0 = 1; 1 Ú 1 = 1, т.е. равенство хотя бы одного аргумента логической единице определяет единичное значение всей функции. На функциональных схемах дизъюнктор обозначается цифрой 1 в правом верхнем углу (рисунок 3.1, б).
Конъюнкция (таблица 3.2) переменных x1 и x2 равна логической 1 в том случае, когда и x1, и x2 равны логической 1 (отсюда название логическое И).
| Таблица 3.1 | Таблица 3.2 | |||||
| x1 | x2 | y | x1 | x2 | y | |

а − инвертор; б − дизьюнктор; в − коньюнктор
Рисунок 3.1 − Функциональное обозначение
Операция логического умножения обозначается точкой или, в буквенных выражениях, никак не обозначается:
y = x1 × x2 = x1 x2.
Графическое обозначение конъюнктора приведено на рисунке 3.1, в. Дизъюнкция, как и конъюнкция, может осуществляться с многими переменными.
3.2 Основные законы алгебры логики
В алгебре логики имеется четыре основных закона:
1. Переместительный, или закон коммутативности для операций сложения и умножения соответственно:
A Ú B = B Ú A;
A B = B A.
2. Сочетательный, или закон ассоциативности для сложения и умножения соответственно:
(A Ú B) Ú C = A Ú (B Ú C);
(A B) C = A (B C).
3. Распределительный, или закон дистрибутивности для сложения и умножения соответственно:
(A Ú B) C = A C Ú B C;
(A B) Ú C = (A Ú C) (B Ú C).
4. Закон двойственности или инверсии (правило де Моргана) сложения и умножения соответственно:

Справедливость этих законов можно доказать с помощью таблиц истинности сложных логических связей, описываемых законом, или с помощью логических преобразований.
Для преобразований логических выражений пользуются легко доказываемыми тождествами:

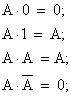

С помощью законов алгебры логики и тождеств могут быть доказаны соотношения, получившие названия правил:
поглощения A Ú A×B = A,
A∙ (A Ú B) = A
и склеивания 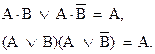
Эти правила широко используют для преобразования переключательных функций с целью их упрощения.
Из правила де Моргана вытекают следствия:

с помощью которых появляется возможность выражать дизъюнкцию через конъюнкцию и отрицание, а конъюнкцию – через дизъюнкцию и отрицание. Законы двойственности справедливы для любого числа переменных.
Формы переключательной функции являются двойственными, если одна получается из другой путем замены всех символов операции И на символы операции ИЛИ и, наоборот, всех нулей на единицы и наоборот. Например, для функции

двойственной функцией будет:
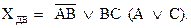
В булевой алгебре при отсутствии в выражении скобок вводится следующий порядок действий: первыми выполняются операции отрицания, далее – конъюнкции, затем – дизъюнкции. Наличие в выражении скобок изменяет обычный порядок действий: в первую очередь должны выполняться операции внутри скобок.
3.3 Элементарные логические функции
Совокупность различных значений переменных называют набором. Булева функция n аргументов может иметь до N = 2n наборов. Поскольку функция принимает только два значения, общее число булевых функций n аргументов равно 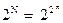 .Таким образом, функция одного аргумента может иметь четыре значения: y = x;
.Таким образом, функция одного аргумента может иметь четыре значения: y = x; 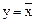 ; y = 1 (константа 1); y = 0 (константа 0). Два аргумента дают 16 значений функции (таблица 3.3).
; y = 1 (константа 1); y = 0 (константа 0). Два аргумента дают 16 значений функции (таблица 3.3).
Любая из этих функций обращается в единицу только на своем наборе, во всех остальных случаях (2n – 1) она равна нулю. Такие функции получили название функций конституенты единицы. Аналогично функция конституента нуля обращается в нуль только на данном наборе, а в остальных случаях она равна единице, т.е. функции взаимно инверсны.
В число шестнадцати функций входят и вырожденные функции:
f0 (x1, x2) = 0 – константа 0; f3 (x1, x2) = x1 – переменная x1;
f 5 (x1, x2) = x2 – переменная x2; f10 (x1, x2) = 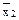 – инверсия x
– инверсия x
f12 (x1, x2) = 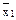 – инверсия x1; f15 (x1, x2) = 1 – константа 1.
– инверсия x1; f15 (x1, x2) = 1 – константа 1.
Таблица 3.3
| x1 | x2 | f0 | f1 | f2 | f3 | f4 | f5 | f6 | |
| f7 | f8 | f9 | f10 | f11 | f12 | f13 | f14 | f15 | |
Остальные десять булевых функций сведены в таблицу 3.4.
Таблица 3.4 − Булевы функци
| Функция | Логическое выражение | Обозначение | Наименование |
| f1(x1, x2) | x1 x2 | x1 L x2 | Конъюнкция, логическое И |
| f7(x1, x2) | x1 + x2 | x1 V x2 | Дизъюнкция, логическое ИЛИ |
| f2(x1, x2) | 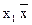 2 2
| x1 D x2 | Запрет по x2 |
| f4(x1, x2) |  x2 x2
| x1 Ñ x2 | Запрет по x1 |
| f11(x1, x2) | 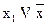 2 2
| x1 ® x2 | Импликация от x2 к x1 |
| f13(x1, x2) | 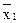 V x2 V x2
| x1 ® x2 | Импликация от x1 к x2 |
| f6(x1, x2) | 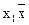 2V 2V  x2 x2
| x1 Å x2 | Сложение по модулю 2 (исключительное ИЛИ) |
| f9(x1, x2) | x1x2 V 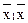 2 2
| x1 º x2 | Равнозначность (эквивалентность) |
Продолжение таблицы 3.4
| f8(x1, x2) | 
| x1 ¯ x2 | Стрелка Пирса (операция ИЛИ-НЕ) |
| f14(x1, x2) | 
| x1 ½ x2 | Штрих Шеффера (операция И-НЕ) |
Дадим краткую характеристику функциям, приведенным в таблице 3.4.
Функция Пирса реализует логическое сложение аргументов с отрицанием:
f8 (x1, x2) = x1 ¯ x2 = 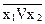 =
= 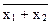 .
.
Следовательно, данная функция инверсна функции дизъюнкции f7 (x1,x2):
f8 (x1, x2) = 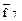 (x1, x2).
(x1, x2).
Функция Шеффера осуществляет логическое умножение с отрицанием
f14(x1,x2) = x1 ½ x2 = 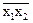 .
.
Эта функция является инверсной по отношению к функции конъюнкции f1 (x1, x2) = x1 x2 :
f14 (x1, x2) = 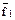 (x1,x2).
(x1,x2).
Функции Пирса и Шеффера связаны между собой соотношениями, аналогичными формулам де Моргана для функций дизъюнкции и конъюнкции:
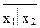 =
= 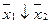 или x1x2 =
или x1x2 = 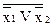 ,
,
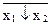 =
=  или x1 V x2 =
или x1 V x2 =  ,
,
поскольку они инверсны по отношению друг к другу:
f8 (x1, x2) =  14 (x1, x2).
14 (x1, x2).
Для функций Пирса и Шеффера справедливы следующие тождества:
x ¯ x = 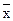 , x ¯ 0 =
, x ¯ 0 = 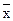 , x ¯ 1 = 0,
, x ¯ 1 = 0,
x ½ x = 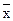 , x ½ 0 = 1,
, x ½ 0 = 1, 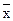 ½ 1 = x.
½ 1 = x.
Графическое изображение функций Пирса и Шеффера показано на рисунке 3.2 а, б соответственно.
Функции запрета и импликации также инверсны по отношению друг к другу. Запрет по x2 f2 (x1, x2) = 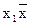 2 является инверсией функции импликации от
2 является инверсией функции импликации от
x1 к x2 f13 (x1, x2) = 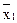 V x2, т.е. x1 D x2 =
V x2, т.е. x1 D x2 = 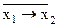
или 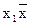 2 =
2 = 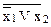 , f2 (x1, x2) =
, f2 (x1, x2) = 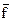 13 (x1, x2).
13 (x1, x2).
Аналогично запрет по x1 функции f4 (x1, x2) = 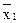 x2 является отрицанием функции импликации от
x2 является отрицанием функции импликации от
x2 к x1 f11 (x1, x2) =  2.
2.
При этом справедливы следующие соотношения: x2 D x1 = x2 ® x1, 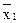 x2 =
x2 = 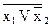 ,
,
f4 (x1, x2) = 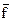 11 (x1, x2).
11 (x1, x2).
Графическое изображение функции запрета приведено на рисунке 3.2.

а) − ИЛИ-НЕ; б) − И-НЕ; в) − импликации; г) − сумма по
модулю два
Рисунок 3.2 − Графическое изображение логических схем
Для импликации не выполняются переместительный и сочетательный законы, поскольку для нее справедливы следующие соотношения:
x1 ® x2 = 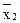 ®
®  ; x1 ® x2 ® x1 = x1.
; x1 ® x2 ® x1 = x1.
Для импликации выполняются следующие тождества:
x ® x = 1, x ® 1 = 1, 0 ® x = 1,
x ® 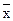 =
= 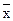 , x ® 0 =
, x ® 0 = 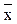 , 1 ® x = 1.
, 1 ® x = 1.
Для функции сложения по модулю два справедливы следующие тождества:
x Å x = 0, x Å 0 = x, x Å 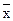 = 1, x Å 1 =
= 1, x Å 1 = 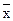 .
.
На рисунке 3.4 г приведено графическое изображение функции неравнозначности (сумма по модулю два).
Запрет по x2
f2 (x1, x2) = 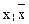 2
2
является инверсией функции импликации от x 2 к x1
f13 (x1, x2) = 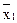 V x2,
V x2,
f2 (x1, x2) = 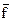 13 (x1, x2).
13 (x1, x2).
Это легко доказывается с помощью правила де Моргана:
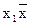 2 =
2 = 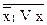 2.
2.
Аналогично, запрет по x1 f4 (x1, x2) =  2, является взаимноинверсным с импликацией от x1 к x2 функции
2, является взаимноинверсным с импликацией от x1 к x2 функции
f11 (x1, x2) = 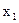 V
V  :
:
f4 (x1, x2) = 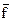 11 (x1, x2),
11 (x1, x2),  x2 =
x2 = 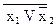 .
.
Функция неравнозначности f6 (x1, x2) является инверсной по отношению к функции эквивалентности f9 (x1, x2):
f6 (x1, x2) = 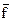 9 (x1, x2),
9 (x1, x2),
 2V
2V 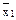 x2 =
x2 = 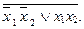
Докажем это равенство, используя правило де Моргана:
(  2V
2V  x2 ) =
x2 ) = 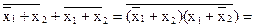
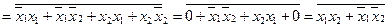 .
.
С помощью функций одной и двух переменных, называемых элементарными логическими функциями, используя принцип суперпозиции (принцип подстановки булевых функций вместо аргументов в другую функцию), можно построить любую сложную булеву функцию.
3.4 Представление переключательных функций
Логические функции, представляющие собой дизъюнкции отдельных членов, каждый из которых есть некоторая функция, содержащая только конъюнкции, называют логическими функциями дизъюнктивной нормальной формы (ДНФ), например:
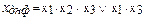 .
.
Если же каждый член дизъюнкции нормальной формы от n аргументов содержит все эти аргументы, часть которых входит в него с инверсией, а часть − без нее, то такая форма представления функции называется совершенной дизъюнктивной нормальной формой (СДНФ):
хСДНФ = х1× х2× х 3 Ú х1×  × х3 Ú х1× х2×
× х3 Ú х1× х2× 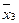 .
.
Каждая конъюнкция этой дизъюнкции включает каждую переменную только один раз в прямом или инверсном виде, обращаясь в единицу при определенном наборе значений переменных, и носит название констинтуента единицы или минтерм.
Логические функции, представляющие собой конъюнкцию отдельных членов, каждый из которых есть функция содержащая только дизъюнкции прямых или инверсных значений аргументов, называются логическими функциями конъюнктивной нормальной формы (КНФ), например:
хКНФ = (х1 Ú  Ú х3)×( х2 Ú
Ú х3)×( х2 Ú 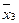 ).
).
Если каждый член конъюнктивной нормальной формы от n аргументов содержит все эти аргументы, часть которых входит в него с инверсией, а часть – в прямом виде, то такая форма представления функции называется совершенной конъюнктивной нормальной формой (СКНФ), например:
хКНФ = (х1 Ú  Ú х3)×( х1 Ú х2 Ú
Ú х3)×( х1 Ú х2 Ú 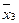 ).
).
Каждая дизъюнкция этой конъюнкции включает каждую переменную только один раз, обращаясь в ноль при определенном наборе переменных, и носит название констинтуента нуля или макстерм.
Правило перехода от табличного задания переключательной функции к ее записи в СДНФ заключается в следующем:
1. Составить минтермы для строк таблицы истинности, на которых функция Х равна 1. Если значение переменной в этой строке равно 0, то в минтерме записывается отрицание этой переменной.
2. Записать дизъюнкцию составленных минтермов, которая будет представлять переключательную функцию в СДНФ.
Это правило называют правилом записи переключательной функции по единицам.
Пусть переключательная функция f (x 1, x 2, x 3) задана таблицей истинности (таблица 3.5).
Таблица 3.5 Таблица истинности f(x 1, x 2, x 3)
| Номер набора | ||||||||
| х 1 | ||||||||
| х 2 | ||||||||
| х 3 | ||||||||
| У (х 1,х 2,х 3) |
Запись этой переключательной функции в СДНФ будет иметь следующий вид:
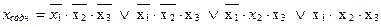 .
.
Алгоритм перехода от табличного значения переключательной функции к ее записи в СКНФ заключается в следующем:
1. Составить макстермы для строк таблицы истинности, на которых функция у равна 0. Если значение переменной (х 1, х 2, х 3) в этой строке равно 1, то в макстерм записывается отрицание этой переменной.
2. Записать конъюнкцию составленных макстермов.
Для таблицы истинности (таблица 3.5) переключательная функция в СКНФ будет иметь вид:
 .Количество переменных, содержащихся в логическом выражении (минтерме или макстерме) – называется рангом. В приведенных примерах макстермы и минтермы имеют третий ранг.
.Количество переменных, содержащихся в логическом выражении (минтерме или макстерме) – называется рангом. В приведенных примерах макстермы и минтермы имеют третий ранг.
Если минтермам (макстермам) присвоить индекс i (порядковый номер в таблице 3.5), то переключательная функция может быть записана:
у СДНФ = М 0 V М 1 V М 3 V М 7,
у СКНФ = m 2 m 4 m 5 m 6 .
Не полностью определенные переключательные функции – функции, для которых не определено их значение хотя бы на одном наборе переменных. Пусть в таблице 3.5 функция не определена на третьем наборе, тогда функция на этом наборе должна быть обозначена знаком Х или буквой Ф (функционал – или комбинация 1 и 0):
х 1 = 0, х 2 = 1, х 3 = 1 y = Ф.
В этом случае при записи функции в СДНФ или СКНФ данному набору можно присвоить значение 0 или 1. Доопределение такой функции производится на разных этапах обработки функции в зависимости от конкретной задачи, например, при минимизации. На практике, как правило, используется запись функций в СДНФ, поскольку она более компактна и наглядна по сравнению с записью в СКНФ. В связи с этим рассмотрим способ перехода от записи функции в ДНФ к СДНФ. Для перехода от ДНФ к СДНФ необходимо в каждый из членов, в которых представлены не все аргументы, ввести сомножители вида 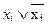 , где x i – отсутствующий в члене аргумент. Так как
, где x i – отсутствующий в члене аргумент. Так как 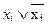 = 1, то такая операция не может изменить значения функции. Покажем переход от ДНФ к СДНФ на примере следующего выражения:
= 1, то такая операция не может изменить значения функции. Покажем переход от ДНФ к СДНФ на примере следующего выражения:
F (x 1, x 2, x 3) = х 1 х 2 Ú х 2 х 3. 
Добавление в члены выражений недостающих аргументов приведет к виду:
F (x 1, x 2, x 3) = х 1 х 2 (х 3 V 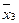 ) V х 2 х 3 (х 1 V
) V х 2 х 3 (х 1 V 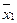 ) =
) =
= х 1 х 2 x3 V x 1 x 2 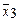 V x 1 x 2 x 3 V
V x 1 x 2 x 3 V 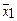 x 2 x 3.
x 2 x 3.
Полученная форма является СДНФ.
3.5 Функционально полные системы переключательных
функций
Система элементарных булевых функций φ 1, φ 2,…., φ m называется функционально полной, или базисом, если любую функцию алгебры логики можно представить в виде их суперпозиции функций. Имея логические элементы, осуществляющие операции f 0 – f 15 , можно выполнить любую сложную функцию. Однако условие наличия 16 различных типов логических элементов, каждый из которых реализует одну из 16 элементарных операций, является условием, достаточным для синтеза логического устройства любой сложности, но не необходимым, т.е. при синтезе можно ограничиваться меньшим набором элементарных функций, взятых из f 0 – f 15. Последовательно исключая из базиса избыточные функции, можно получить минимальный базис. Под минимальным базисом понимают такой набор функций, исключение из которого любой функций превращает этот набор в неполную систему функций.
Возможны различные базисы и минимальные базисы, различающиеся числом входящих в них функций и видом этих функций. Выбор того или иного базиса для синтеза логического устройства связан с тем, насколько просто, удобно и экономично технически выполнять узлы, реализующие элементарные функции, которые входят в выбранный базис, и в целом все логическое устройство.
Функционально полными системами являются базисы:
И, ИЛИ, НЕ – базис 1, И-НЕ – базис 4, ИЛИ, НЕ – базис 3,
И, НЕ – базис 2, ИЛИ-НЕ – базис 5, И-ИЛИ, НЕ – базис 6.
Базис И, ИЛИ, НЕ принято называть основным, так как любая сложная переключательная функция может быть записана в СДНФ или СКНФ. Базис И, ИЛИ, НЕ является избыточной системой, так как возможно исключение из него некоторых функций. Например, используя правило Де Моргана, можно исключить либо функцию И (получим базис 3), заменяя ее ИЛИ и НЕ, либо ИЛИ (получим базис 2), заменяя ее на И и НЕ.
Базисы И, НЕ и ИЛИ, НЕ называют универсальными. Эти базисы приобрели важное значение в связи с широким использованием интегральных логических элементов при построении логических устройств.
Структуры логических элементов НЕ, И, ИЛИ, состоящие из элементов Шеффера, приведены на рисунке 3.3.
Схема отрицания НЕ реализована на использовании следующего соотношения: 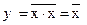 .
.
Схема логического умножения использует принцип двойной инверсии:
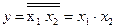 .
.
Схема логического сложения двух двух сигналов базируется на использовании закона отрицания:
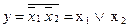 .
.
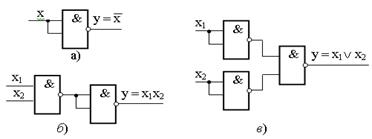
а − элемент НЕ ; б − элемент И; в − элемент ИЛИ
Рисунок 3.3 − Реализация схем
Cтруктуры логических элементов НЕ, ИЛИ, И, выполненные на логических элементах ИЛИ – НЕ приведены на рисунке 3.4. Схема логической инверсии (рисунок 3.4, а) −  ,
,
логического сложения (рисунок 3.4, б) – 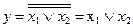 ,
,
логического умножения (рисунок 3.4, в) – 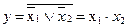 .
.
Связующим звеном между реальным элементом и его переключательной функцией служит полярность логики. Различают положительную и отрицательную логику. При положительной логике в качестве логической единицы принят высокий уровень сигнала, при отрицательной логике – низкий уровень сигнала.
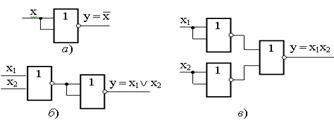
а − элемент НЕ; б − элемент ИЛИ; в − элемент И
Рисунок 3.4 − Реализация схем
Из принципа дуальности следует, что одно и то же логическое выражение может быть представлено двояко, например,
y = x 1 x 2 и 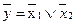 .
.
Это значит, что один и тот же элемент будет реализовывать с точки зрения положительной логики функцию конъюнкции, а с точки зрения отрицательой логики – дизъюнкцию.
В дальнейшем в качестве единицы будет принят высокий уровень напряжения (положительная логика).
3.6 Минимизация переключательных функций
Минимизация– процесс приведения булевых функций к такому виду, который допускает наиболее простую, с наименьшим числом элементов, физическую реализацию функции. Частная задача минимизации булевой функции сводится к такому представлению заданной функции, которое содержит наименьшее возможное число букв и наименьшее возможное число операций над ними, так как каждой элементарной логической функции соответствует определенный физический элемент.
Оценить различные представления одной и той же булевой функции, например ДНФ, можно по количеству входов логических элементов, реализующих заданную функцию. Такую оценку реализации булевой функции называют ценой реализации функции по Квайну (Мак-Класки) или ценой покрытия булевой функции системой логических элементов. Для минимизации переключательных функций применяют различные методы: последовательного исключения переменных с помощью законов алгебры логики, методом Квайна, карт Карно (Вейча) и др.
Метод последовательного исключения переменных с помощью законов и тождеств алгебры логики является наиболее простым методом минимизации. Любое упрощение переключательной функции происходит при вынесении за скобки общих множителей из минтермов, суммирование которых приводит к исключению отдельных переменных. Процесс подбора пары минтермов, сопровождающийся понижением ранга переменной, называется склеиванием минтермов.
В качестве примера рассмотрим минимизацию переключательной функции yСДНФ =  методом последовательного исключения переменных. Сгруппируем первый и второй минтерм, второй и третий:
методом последовательного исключения переменных. Сгруппируем первый и второй минтерм, второй и третий:
Y= 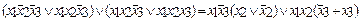 .
.
Учитывая, что 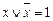 , получим сокращенную нормальную форму:
, получим сокращенную нормальную форму: 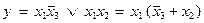 .
.
Конъюнкции 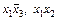 , входящие в такую сокращенную нормальную форму, называются импликантами.
, входящие в такую сокращенную нормальную форму, называются импликантами.
Под простой импликантой булевой функции f (x1, x2…xn) понимается всякое элементарное произведение P = x1·x2…xn, где k < n, которое является импликантой функции f и никакая собственная часть этого произведения в функцию f не входит, т.е. простые импликанты – элементарные конъюнкции наименьшего ранга, входящие в данную булеву функцию.
Сокращенной дизъюнктивной нормальной формой булевой функции называется такая функция, которая равна дизъюнкции всех своих простых импликант. Несмотря на то, что сокращенная ДНФ булевой функции содержит меньшее число букв, чем СДНФ этой функции, она в большинстве случаев допускает упрощение за счет поглощения некоторых простых импликант дизъюнкцией других простых импликант. В случае, если в дизъюнкции простых импликант, представляющих заданную функцию, ни одну из импликант исключить нельзя, то такую дизъюнкцию называют тупиковой дизъюнктивной нормальной формой. Выявление групп минтермов, отличающихся между собой комбинациями одних и тех же переменных, при большом числе переменных является задачей довольно сложной. Кроме того, некоторые минтермы могут входить одновременно в несколько групп и, следовательно, задача образования групп не может быть решена однозначно. Группируя минтермы различными способами, можно получить различные упрощенные формы заданной функции. Возможно, что получена одна из тупиковых форм, но нельзя быть уверенным, что она является минимальной.
3.6.1 Минимизация логических функций методом Квайна
Метод Квайнаприменяется для переключательных функций невысокого ранга при условии, что исходные функции заданы в СДНФ. Метод Квайна выполняется в два этапа: на первом этапе осуществляется переход от канонической формы СДНФ к сокращенной, на втором этапе – переход от сокращенной формы логического выражения к минимальной.
Пусть задана функция:
yСДНФ = 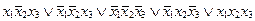 .
.
На первом этапе ведется нахождение сокращенной нормальной формы функции. Для этого составляется таблица 3.6, с помощью которой подбираются пары минтермов, отличающихся друг от друга значением лишь одной переменной.
Таблица 3.6
| Минтермы | 
| 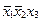
| 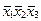
| 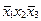
| 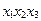
|

| 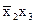
| 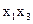
| |||
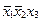
| 
| 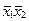
| |||
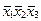
| 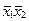
| 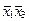
| |||
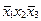
| 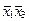
| ||||
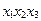
| 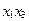
|
Сумма двух минтермов дает импликанту второго ранга и эта импликанта записывается в таблицу 3.7 на пересечении склеиваемых минтермов.
Таблица 3.7
| Минтермы Импликанты | 
| 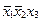
| 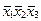
| 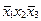
| 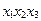
|

| + | + | |||
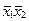
| + | + | |||
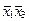
| + | + | |||
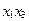
| + | + |
Сумма найденных импликант представляет сокращенную ДНФ исходной функции:
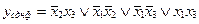 .
.
На втором этапе ведется поиск лишних членов в полученной сокращенной форме, исключение которых из выражения функции не повлияет на ее значение. Для этого составляется таблица 3.6, число строк которой равно числу полученных импликант, а в столбцах расположены все минтермы исходной функции. На пересечении строк и столбцов проставляются метки, если простая импликанта входит в данный минтерм.
Каждой переключательной функции соответствует только одна нормальная форма, тогда как минимальных форм может быть несколько. Минимальные формы из таблицы 3.6 могут быть получены следующим образом. Минимальная форма переключательной функции должна содержать все импликанты, перекрывающие все минтермы заданной функции. Для рассматриваемой функции можно получить две минимальные формы:
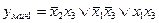
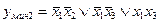 ,
,
которые не совпадают с полученной ранее тупиковой формой. Достоинством метода Квайна является четкость сформулированных правил проведения отдельных операций, благодаря чему возможно использование ЭВМ для минимизации достаточно сложных функций.
3.6.2 Минимизация логических функций с помощью карт Карно
Метод минимизации карт Карно (Вейча) находит широкое применение для минимизации переключательных функций 3 – 6 аргументов, поскольку обеспечивает простоту получения результата. На рисунке 3.5, а, б, в приведены карты Карно для трех f (x3 x2 x1), четырех f(x4 x3 x2 x1) и пяти аргументов f(x5 x4 x3 x2 x1) с нанесенными на них номерами минтермов функции f(x4 x3 x2 x1), где x5 – старший разряд, x1 – младший. Аргументы функции делятся на две группы, комбинации значений аргументов одной группы приписываются столбцам таблицы, комбинации значений аргументов другой группы – строкам таблицы. Столбцы и строки обозначаются комбинациями, соответствующим последовательности чисел в коде Грея, поскольку в этом случае склеивающиеся клетки находятся рядом.
Карта Карно определяет значение функции на всех возможных наборах аргументов и, следовательно, является таблицей истинности. Карты Карно компактны и удобны для поиска склеиваемых членов переключательной функции СДНФ. Объясняется это тем, что два любых минтерма, находящихся в клетках, расположенных рядом друг с другом, являются соседними. Они могут быть заменены одной конъюнкцией, содержащей на одну переменную меньше.
Группа из четырех минтермов, расположенных в соседних клетках, может быть заменена конъюнкцией, содержащей на две переменные меньше. В общем случае группа из 2k соседних клеток будет заменена одной конъюнкцией с n – k аргументами, при общем числе переменных равным n.
Минимизацию переключательных функций будем вести на основании следующих правил:
– все клетки, содержащие 1, объединяются в замкнутые области;
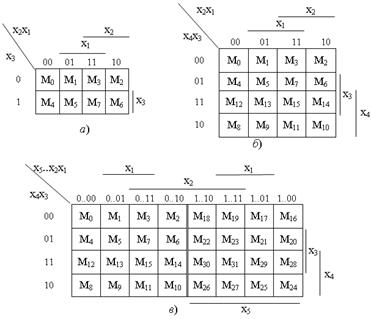
Рисунок 3.5 − Карты Карно для: а −3-х аргументов; б − 4-
Дата добавления: 2020-03-17; просмотров: 1002;











