Второй критерий оптимальности распределения поставок.
Реализация распределительного метода связана с некоторыми техническими трудностями. Они состоят в том, что зачастую приходится строить много различных циклов, пока не будет обнаружен
план с отрицательной оценкой. Поэтому распределительный метод был
модифицирован так, что изменился алгоритм выполнения наиболее трудоемкой части — определения оценки свободной клетки — и получил название метода потенциалов.
Рассмотрим m + n произвольных чисел, поставив в соответствие каждому из пунктов отправления А1 некоторое число а1 (i=1,2...m)
и каждому из пунктов назначения Bj, некоторое число Bj,(j = 1,2...n).
Числа а1,а2...аm называются потенциалами пунктов отправления, а числа B1,B2...BN — потенциалами пунктов назначения.
Потенциалы выбираем из следующего условия: для всех базисных клеток таблицы перевозок сумма соответствующих потенциалов должна
быть равна стоимости перевозки единицы груза, то есть:
a1+bj=cij (27)
система линейных алгебраических уравнений (27) состоит из n+m-1 уравнения с m+n неизвестными. Доказано, что эта система совместна и неопределенна. Ее ранг r = m+n-1. Для определенности считаем а1 свободной переменной и берем базисное решение системы (27) при а1 =0.
Установим новый критерий оптимальности решения ТЗ. Рассмотрим свободную клетку с простейшим циклом пересчета (рис. 19).
Алгебраическая сумма стоимостей свободной клетки 
Все вершины цикла пересчета свободней клетки (i,j), кроме
самой клетки (i,j), базисные. Согласно (27) для базисных клеток имеем
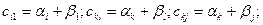
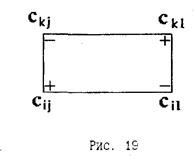
тогда:
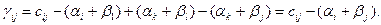
Из первого критерия оптимальности следует, что, если 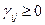 для всех свободных клеток, то решение оптимально.
для всех свободных клеток, то решение оптимально.
Согласно (28) и первому критерию оптимальности:
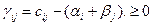 .
.
откуда следует второй критерий оптимальности:
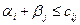
Второй критерии оптимальности решения ТЗ: если для всех свбодных клеток таблицы перевозок сумма соответствующих потенциалов не превосходит стоимости перевозки единицы груза, то данное распределение поставок оптимально по критерию стоимости.
4.4. 5. Решение ТЗ методом потенциалов.
1. Проверяем, является ли ТЗ задачей с правильным балансом.
2. Находим исходное допустимое базисное решение ТЗ методом СЗУ или МНС.
3. Находим потенциалы  , решая систему (27). Записываем их в таблицу перевозок.
, решая систему (27). Записываем их в таблицу перевозок.
4. Находим суммы соответствующих потенциалов для свободных клеток и помещаем их в правый нижний угол свободных клеток таблицы перевозок, обводя в кружок.
5. Проверяем выполнение второго критерия оптимальности: сравниваем значение стоимости с числом в кружке для всех свободных клеток.
6. Если  для всех свободных клеток, то данное распределение поставок оптимально. Если для одной или нескольких клеток
для всех свободных клеток, то данное распределение поставок оптимально. Если для одной или нескольких клеток 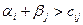 , то переходим к пункту (7).
, то переходим к пункту (7).
7. Определяем ту свободную клетку, для которой 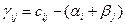 имеет наибольшее по модулю отрицательное значение. Определяем для этой свободной клетки цикл пересчёта и производим по нему сдвиг на число ε. Строим новую таблицу перевозок.
имеет наибольшее по модулю отрицательное значение. Определяем для этой свободной клетки цикл пересчёта и производим по нему сдвиг на число ε. Строим новую таблицу перевозок.
8. Переходим к пунктам 3-7 и повторяем процесс до тех пор, пока не будет выполнен второй критерий оптимальности решения ТЗ для всех свободных клеток.
Пример. Определяем потенциалы  решая систему:
решая систему:
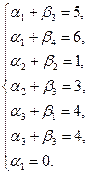
В результате получаем 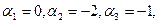
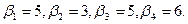
Заносим все значения потенциалов в таблицу, вычисляем сумму
потенциалов свободных клеток и помещаем ее в правый нижний угол свободной клетки, обводя в кружок (табл. 9).
Проверяем выполнение критерия оптимальности. Единственная
клетка, для которой критерий оптимальности не выполнен, - (1,2):

Определяем для клетки (1,2) цикл пересчета, находим число
e=min{20,50,80}=20 и производим сдвиг по циклу на число e=20. Строим новую таблицу перевозок (табл. 10).
Таблица 9
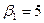
| 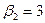
| 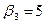
| 
| ||||
| Пункт отправления | Пункт назначения | B1 | B2 | B3 | B4 | запасы | |
| A1 |  5 5
 5 5
|   2+
3 2+
3
| 5- 20 | 6 40 | ||

| A2 | 3
 3 3
| 1 -80 | 3 +0 | 7
 4 4
| ||
| A3 | 4 40 | 5
 2 2
| 4 30 | 6
 5 5
| ||
| потребности |
Таблица 10
| 
| 
| 
| ||||
| Пункт отправления | Пункт назначения | B1 | B2 | B3 | B4 | запасы | |
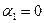
| A1 |  5 5
 4 4
| 2+ 20 | 5-
 4 4
| 6 40 | ||

| A2 | 3
 3 3
| 1 60 | 3 20 | 7
 5 5
| ||
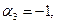
| A3 | 4 40 | 5
 2 2
| 4 30 | 6
 6 6
| ||
| потребности |
Следующая итерация начинается с определения потенциалов. Для этого имеем систему линейных алгебраических уравнений:

Решая систему получаем 
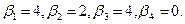
Заносим все значения потенциалов в таблицу, вычисляем сумму
потенциалов свободных клеток и помещаем ее в правый нижний угол свободной клетки, обводя в кружок.
Проверяем выполнение критерия оптимальности. Очевидно, что критерий оптимальности выполнен - для всех клеток  .
.
Данное распределение поставок оптимально по критерию стоимости.
Ответ:
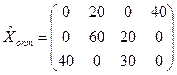 .
.
fmin=2*20+6*40+1*60+3*20+4*40+4*30=680.
Замечание. Распределение поставок, полученное методом потен-
циалов, отличается от распределения поставок, полученного распределительным методом. хотя значения функции цели на этих обоих решениях одинаковы. Это говорит о том, что решение задачи не единственное. Мы условились называть его альтернативным.
4.5. ТЗ по критерию стоимости с неправильным балансом
Задача с неправильным балансом сводится к задаче с правильным балансом путем введения так называемых фиктивныхпунктов отправления и фиктивныхпунктов назначения.
Случай 1. Пусть

то есть суммарная мощность поставщиков больше суммарной мощности потребителей.
Вводим фиктивный пункт назначения Bn+1. потребности в грузе
которого составляют

Стоимости перевозок из всех пунктов отправления в фиктивный пункт назначения Bn+1 полагаем равными нулю: c1n+1, c2n+1, … cmn+1=0.
Получим ТЗ с правильным балансом:
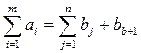
Пример. Найти оптимальное распределение поставок для Т3, заданной таблицей 11.
Таблица 11
| Пункт отправления | Пункт назначения | B1 | B2 | B3 | запасы |
| A1 | 1 | 3 | 2 | ||
| A2 | 2 | 1 | 3 | ||
| потребности |
Решить задачу самостоятельно.
Ответ.
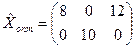 , fmin=42.
, fmin=42.
Из пункта А2 будет отправлено 5 единиц груза.
Случай 2. Пусть
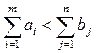
Вводим фиктивный пункт отправления Am+1, запас груза в котором:
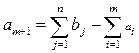 ,
,
Стоимости перевозок из фиктивного пунктa отправления Am+1 во все пункты назначения полагаем равными нулю: c1m+1, c2m+1, … cm+1n=0.
Получим ТЗ с правильным балансом:
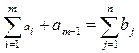
Пример. Найти оптимальное распределение поставок для ТЗ, заданной таблицей 12.
таблица 12.
| Пункт отправления | Пункт назначения | B1 | B2 | B3 | запасы | |
| A1 | 3 | 1 | 5 | 2 | ||
| A2 | 4 | 6 | 7 | 3 | ||
| A3 | 2 | 8 | 4 | 5 | ||
| потребности |
Задачу решить самостоятельно.
Ответ.
 , fmin=162.
, fmin=162.
Потребности пункта B3 будут не удовлетворены на 5 единиц.
Замечание. При нахождении исходного решения ТЗ с неправильным балансом МНС следует фиктивные пункты учитывать в самую последнюю очередь, то есть выбирать наименьшую стоимость в первую очередь среди стоимостей реальных пунктов.
Внимание к ТЗ обусловлено тем, что задачи подобного типа и многие другие ЗЛП, во-первых, часто встречаются в практических расчётах, и, во-вторых, к ним сводятся многие другие задачи линейного программирования: сетевая задача, задача о назначениях, задача календарного планирования.
Дата добавления: 2020-02-05; просмотров: 716;











