Постановка двойственных задач.
Рассмотрим две задачи линейного программирования.
I. II.
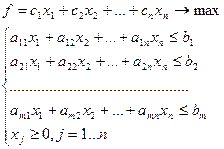
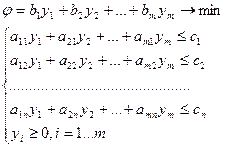
Эти задачи образуют пару симметричные двойственных задач. Особенности и общие правила составления двойственных задач:
1) В исходной задаче (I) во всех ограничениях члены, содержащие переменные, должны стоять в левой части неравенств, а свободные члены - в правой.
2) Все неравенства в ограничениях исходной задачи должны
иметь одинаковый знак, причем " 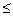 " в задачах максимизации и "
" в задачах максимизации и " 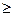 " в
" в
задачах минимизации.
3) Свободные члены ограничений исходной задачи являются коэффициентами при неизвестных в функции цели двойственной задачи.
4) Если исходная задача - задача максимизации, то двойственная к ней - минимизации.
5) Если в исходной задаче неравенство ограничений " 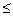 ", то в двойственной задаче - "
", то в двойственной задаче - " 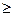 ".
".
6) Число переменных исходной задачи равно числу ограничений
двойственной задачи.
7) Матрицы из коэффициентов при неизвестных в ограничениях
прямой и двойственной задач транспонированы одна относительно
другой.
Пример. Составить задачу, двойственную данной:
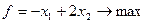
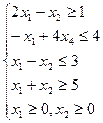
Решение. так как исходная задача - задача максимизации, то приведем все неравенства системы ограничений к виду " 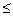 ", умножив неравенства вида "
", умножив неравенства вида " 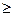 " на (-1) и поменяв знак неравенства на противоположный:
" на (-1) и поменяв знак неравенства на противоположный:
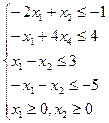
Составим таблицу из расширенной матрицы системы ограничений, добавив к ней последней строкой коэффициенты при неизвестных в целевой функции:
| -2 | -1 | |
| -1 | ||
| -1 | ||
| -1 | -1 | -5 |
| -1 | f |
Составим таблицу, поменяв, в предыдущей строки на столбцы, а f – на φ
| -2 | -1 | -1 | -1 | |
| -1 | -1 | |||
| -1 | -5 | φ |
Формулируем двойственную задачу:
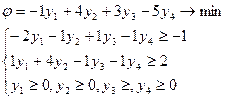
Дата добавления: 2020-02-05; просмотров: 636;











