Основные теоремы двойственности.

Связь между оптимальными решениями двойственных задач уста­навливается с помощью теоремы двойственности:

Теорема 1. Если одна из двойственных задач имеет единствен­ное оптимальное решение, то и другая задача также имеет единс­твенное оптимальное решение, причем экстремальные значения функ­ции цели этих задач совпадают:

f_max = φ_min

Если функция цели одной из задач неограниченна, и задача не имеет оптимального решения, то двойственная к ней задача не имеет ни одного допустимого решения.

Теорема 2. Если в оптимальном плане исходной задачи значение какой-либо j-й переменной строго положительно, то соответствующее j-e ограничение двойственной задачи на ее оптимальном плане обра­щается в строгое равенство.

Если оптимальное решение исходной задачи обращает какое-либо 1-е ограничение в строгое неравенство, то соответствующая 1-я пе­ременная в оптимальном решении двойственной задачи равна нулю.

Замечание. В теореме 2 исходной задачей считаем ту, которую решали.

Теорема 3. Значение целевой функции задачи максимизации для любого ее плана не превосходит по величине значения целевой функ­ции двойственной к ней задачи минимизации для любого ее плана:

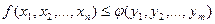
где 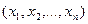- произвольный план задачи максимизации;
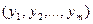- произвольный план задачи минимизации,

Теорема 4. (критерий оптимальности планов двойственных задач). Для того, чтобы планы двойственных задач 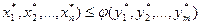были оптимальными, необходимо и дос­таточно, чтобы значения функции цели на этих планах были равны.

Пользуясь этими теоремами, можно, зная решение одной задачи, найти решение задачи, двойственной к ней, не решая последней.

Пример. Найти решение данной задачи:

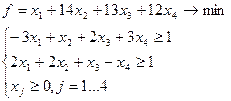
по решению двойственной, используя теоремы двойственности.

Решение. Составим задачу, двойственную данной:

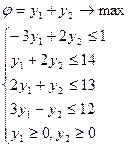
Из этих двух задач легче решить вторую. Решая ее графически, получаем:

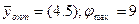
Построим решение данной задачи, используя теорему двойственности.

По теореме 1 данная задача имеет единственное оптимальное решение и f_min = φ_max= 9.

По теореме 2 (часть 1) :

так как y₁=4 > 0, то -3x₁+х₂+2х₃+3x₄ = 1;

так как у₂=5 > 0, то 2x₁+2х₂+х₃-x₄=1.

Таким образом, для определения компонент оптимального плана данной задачи имеем систему уравнений:

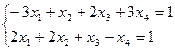
По теореме 2 (часть 2): подставим у_опт в систему ограничений

второй задачи.

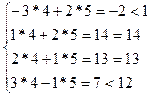
Так как первое и последнее ограничения обратились в строгие неравенства, то x₁ = х₄ = 0, и система для определения компонент оптимального плана данной задачи имеет вид:

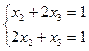
Решая ее, получаем: х₂ = х₃ = 1/3.

Таким образом, решение данной задачи имеет вид:

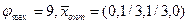
<h» = 9; ХоПТ = (0,1/3,1/3,0).

Замечание. К решению двойственных задач прибегают в том слу­чае, когда двойственная задача решается легче, чем исходная.

Теория двойственности оказалась полезной для проведения ка­чественных исследований задач линейного программирования.

4. ТРАНСПОРТНАЯ ЗАДАЧА ПО КРИТЕРИЮ СТОИМОСТИ И ЕЕ РЕШЕНИЕ.

Постановка ТЗ.

В главе 1 была дана постановка ТЗ по критерию стоимости, для
двух поставщиков и трех потребителей. Обобщая эту задачу на m
поставщиков и п потребителей, получим следующую математическую
постановку ТЗ:

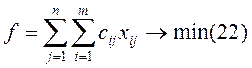
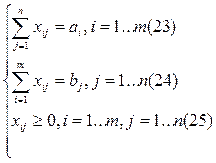
ТЗ представляет собой задачу линейного программирования с числом переменных m*n и числом ограничений равенств m + n. Усло­вие (23) гарантирует полный вывоз груза из всех пунктов отправле­ния, а условие (24) означает полное удовлетворение спроса.

Если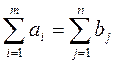

то ТЗ называется задачей с правильным балансом или закрытой задачей, в противном случае ТЗ называется задачей с неправильным ба­лансом или открытой задачей.

Равенство (26) является необходимым и достаточным условием совместности системы уравнений (24), (25) в области допустимых решений и, следовательно, разрешимости задачи.

Рассмотрим закрытую ТЗ. Эта задача может быть решена симп­лекс-методом, как любая ЗЛП. Однако, специфичная форма системы ограничений данной задачи позволяет существенно упростить обычный симплекс-метод и разработать более эффективные вычислительные методы. Модификация симплекс-метода применительно к ТЗ называется распределительным методом.

Некоторые определения и теоремы:

Определение. Набор переменных {x_ij}, удовлетворяющих условиям (23) - (25), записывается в виде матрицы:

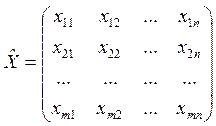
Матрица 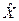называется планом перевозок, а переменные х_ij - перевозками.

Определение. Всякое неотрицательное базисное решение системы линейных уравнений (23), (24), определяемое матрицей 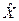, называет­ся опорным планом ТЗ.

Определение. Опорный план 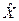, при котором функция (22) при­нимает свое минимальное значение, называется оптимальным опорным планом или просто оптимальным планом ТЗ.

Определение. Матрица, составленная из стоимостей на перевоз­ку единицы груза от i-го поставщика к j-му потребителю, называет­ся матрицей стоимостей (матрицей коэффициентов затрат, матрицей тарифов, матрицей транспортных издержек).

Определение. Таблица, составленная из мощностей поставщиков и потребителей, а также из коэффициентов затрат, называется таб­лицей поставок или таблицей перевозок (коэффициенты затрат ста­вятся в левом верхнем углу соответствующей клетки таблицы).

Подобно тому, как это было в симплекс-методе, в распредели­тельном методе решение ТЗ состоит из следующих основных этапов:

- определение исходного допустимого базисного решения задачи
(первоначального распределения поставок, первоначального опорного
плана);

- оценка этого плана по критерию стоимости:

- переход к следующему, "лучшему" плану путем замены одной
из базисных переменных на свободную.

-