Первый критерий оптимальности распределения поставок.

Пусть известно некоторое исходное допустимое базисное решение ТЗ, построенное методом МНС или СЗУ. Попытаемся «улучшить» это решение, если возможно, перераспределяя поставки, с использованием операции сдвига по циклу на число e.

Выберем любую свободную клетку таблицы перевозок, например (i₀,j₀), построим для этой свободной клетки цикл перерасчёта и произведём по выбранному циклу операцию сдвига по циклу на число e.

В результате этой операции исходное решение системы ограничений ТЗ переходит в другое решение этой системы.

Рассмотрим простейший пример пересчёта свободной клетки (рис. 17).

После сдвига по циклу на число e получаем следующее распределение поставок в клетках данного цикла (рис. 18).

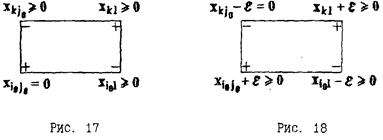
Чтобы после сдвига по циклу полученное решение было допустимым, число e нужно выбрать наименьшим из чисел, стоящих в отрицательных вершинах цикла. Пусть наименьшим будет x_{i j 0.}

e=min{ x_{i 0 1}, x_{k j 0}}= x_{k j 0}.

После сдвига по циклу на число e количество базисных клеток этого цикла должно быть также равно трём. Действительно, свободная клетка с поставкой x_{i0 j0}=0 станет базисной с поставкой x_{i0 j0}=ε, а в свою очередь, клетка с номером x_{k j0} станет свободной с поставкой x_{k j0}=0. Поставки в остальных клетках в соответствии с определением операции сдвига по циклу на число ε либо увеличатся на ε, либо уменьшатся на ε в зависимости от знака вершины означенного цикла.

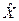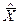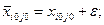
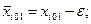
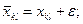
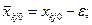
Пусть - исходное допустимое базисное решение транспортной задачи, а - допустимое базисное решение, полученное после сдвига по циклу пересчёта свободной клетки (i₀,j₀) на число ε. При этом 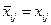для всех клеток (i,j), не входящих в цикл пересчёта свободной клетки (i₀,j₀).

Сравним значения функции цели на этих решениях:

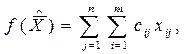
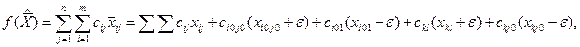
причём суммирование в первом слагаемом ведётся по тем номерам, которые не входят в цикл пересчёта свободной клетки (i₀,j₀).

Очевидно,

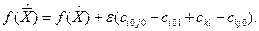
Определение.Число 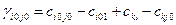называется алгебраической суммой стоимостей по циклу пересчёта свободной клетки (i₀,j₀) или оценкой свободной клетки (i₀,j₀).

Итак,

,

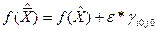где .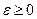

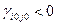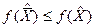Если , то . В этом случае значение функции цели при переходе к новому решению может уменьшиться.

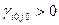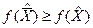Если , то . В этом случае значение функции цели при переходе к новому решению может увеличиваться или не изменится.

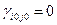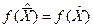Если , то . В этом случае значение функции цели при переходе к новому решению может не изменится.

Отсюда получаем первый критерий оптимальности решения ТЗ:
если для всех свободных клеток таблицы перевозок алгебраическая сумма стоимостей по циклу пересчета неотрицательна, то есть 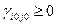, то данное решение транспортной задачи оптимально по критерию стоимости.