УРАВНЕНИЕ ГИББСА–ГЕЛЬМГОЛЬЦА.

В изолированных системах энтропия только увеличивается и при равновесии достигает максимума. Поэтому она может быть использована в качестве критерия протекания самопроизвольных процессов в таких системах. Однако на практике большинство процессов происходит в неизолированных системах, вследствие чего для них надо выбрать свои критерии направления самопроизвольных процессов и достижения равновесия в этих системах. Такими критериями являются другие термодинамические функции, отличные от энтропии и внутренней энергии. Они подобраны таким образом, что с их помощью можно определить в явной форме все термодинамические параметры изучаемой системы. Все они являются функциями состояния и при переходе системы из одного положения в другое меняются однозначно. При достижении системой равновесного состояния каждая из функций проходит через минимальное значение. Такие свойства обуславливают широкое применение этих функций при аналитическом методе решения различных задач термодинамических исследований.

Следует отметить, что такие функции часто называют характеристическими. Характеристической функцией называется такая функция состояния системы, посредством которой и её производных могут быть выражены в явной форме все термодинамические свойства системы.

Согласно первому закону термодинамики:

dA = dQ – dU.(2.15)

Подставив сюда извесное соотношение dQ ≤ TdS, получим

dA ≤ TdS – dU, (2.16)

где знак равенства относится к обратимым равновесным процессам, а знак неравенства — к необратимым. Проинтегрируем (2.16) при Т = const:

A_T ≤ T(S₂ – S₁) – (U₂ – U₁) = (U₁ – TS₁) – (U₂ – TS₂). (2.17)

Функция (U – TS) играет большую роль при изучении равновесия в изотермических процессах. Её называют изохорно-изотермическим потенциалом или энергией Гельмгольца и обозначают символом F. При этом для всякого изотермического процесса:

dF = dU – TdS, (2.18)

∆F = ∆U – T∆S, (2.19)

а максимальная работа в изотермическом процессе

(A_Т)_max = –∆F. (2.20)

Функция F определяет направление и предел течения самопроизвольных процессов, протекающих при постоянных температуре и объёме.

Близкой к изохорно-изотермическому потенциалу является функция, определяющая направление и предел самопроизвольного протекания процессов для систем, находящихся при постоянных температуре и давлении. Эта функция называется изобарно-изотер-мическим потенциалом или энергией Гиббса, обозначается символом G и определяется как

G = H – TS. (2.21)

или

G = U – TS + pV = F + pV. (2.22)

Пусть р = const, тогда

A_T ≤ –∆F = F₁ – F₂, (2.23)

A_T¢ + p(V₂ – V₁) ≤ F₁ – F₂,(2.24)

A_T¢ ≤ (F₁+pV₁) – (F₂ + pV₂) = G₁ – G₂, (2.25)

где A_T¢ – полезная работа (любая работа кроме работы расширения). Тогда

A_T¢ ≤ –∆G.(2.26)

При этом для изотермических процессов

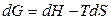, (2.27)

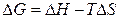, (2.28)

и максимальная работа в изотермическом процессе

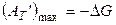, (2.29)

где

,

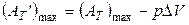т.е. максимальная полезная работа равна максимальной работе изотермического процесса за вычетом работы против сил внешнего давления. Функции G и F называются термодинамическими потенциалами, потому что в определённых условиях стремятся к минимуму при протекании самопроизвольных процессов.

Пусть 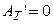, тогда

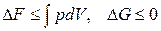. (2.30)

1). Система при T, V = const 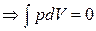, т. е. ΔF ≤ 0. Условие равновесия в изохорно-изотермической системе: dF = 0, ΔF = 0, F = F_min.

2). Система при р, T = const. Тогда 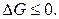Условие равновесия в изобарно-изотерми-ческой системе: dG = 0, ΔG = 0, G = G_min.

Вывод: в системах, находящихся при постоянных температуре и объёме, самопроизвольно могут протекать только те процессы, которые сопровождаются уменьшением энергии Гельмгольца F, причем пределом их протекания, т.е. условием равновесия, является достижение некоторого минимального для данных условий значения функции F; в системах же, находящихся при постоянных температуре и давлении, самопроизвольно могут протекать только те процессы, которые сопровождаются уменьшением энергии Гиббса G, причём пределом их протекания, т.е. условием равновесия, служит достижение некоторого минимального для данных условий значения функции G.

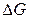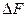Получим соотношения, которые описывают зависимость и от температуры. В общем случае (и для химических реакций):

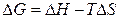, (2.31)

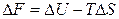. (2.32)

Функция состояния обладает свойствами полного дифференциала, т.е. если 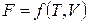, то

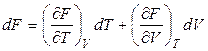. (2.33)

С другой стороны:

F = U – TS, (2.34)

dF = dU – TdS – SdT. (2.35)

С учетом того, что

dU = 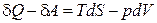,(2.36)

получаем

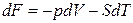. (2.37)

При сравнении уравнений (2.37) и (2.33) видно, что

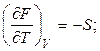
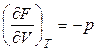, (2.38)

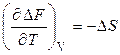. (2.39)

Аналогично для 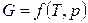, получаем:

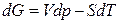, (2.40)

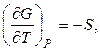
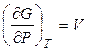, (2.41)

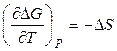. (2.42)

Подставляя соотношения (2.39) и (2.42) в уравнения (2.31) и (2.32), соответственно, получаем:

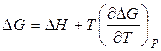, (2.43)

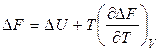. (2.44)

Последние два равенства и есть искомые зависимост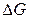и и 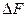от температуры и их называют уравнениями Гиббса-Гельмгольца.