РАСЧЕТ ХИМИЧЕСКОГО ПОТЕНЦИАЛА.

Для системы, состоящей из одного вещества, справедливо:

, .

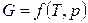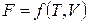Если система состоит из нескольких компонентов, то

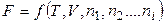, (2.46)

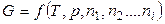, (2.47)

где n_i – число молей i-го компонента. Любая экстенсивная функция состояния является функцией количества вещества в системе.

Продифференцируем (2.46) и (2.47) по n_i:

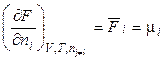, (2.48)

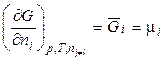, (2.49)

где μ_i – химический потенциал i-го компонента в системе. Его ещё называют парциальной мольной энергией Гиббса (парциальная термодинамическая функция Гиббса) или парциальной мольной энергией Гельмгольца (парциальная термодинамическая функция Гельмгольца), т.к. 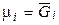и .

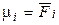Можно дать следующее определение химического потенциала:

химический потенциал равен приращению энергии Гиббса (или любой другой характеристической функции) при увеличении массы данного вещества на 1 моль, если массы всех остальных веществ, температура или давление (или другие естественные переменные для других функций) остаются постоянными.

Любая энергетическая характеристика есть произведение интенсивного фактора на экстенсивный. В нашем случае μ_i – интенсивный параметр, а n_i – экстенсивный.

Тогда

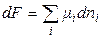при V, T = const,(2.50)

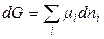при T, p = const. (2.51)

Введение некоторого количества dn_i молей i–го компонента при постоянном количестве других компонентов и постоянных Т и р будет увеличивать значение энергии Гиббса на величину 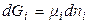. Аналогичные изменения будут вызваны прибавлением других компонентов. Общее изменение энергии Гиббса системы равно:

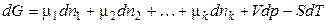, (2.52)

или, в общем случае,

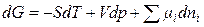, (2.53)

которое получило название фундаментального уравнения Гиббса.

Для любой химической реакции:

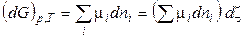, (2.54)

где 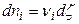( 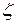– химическая переменная или степень протекания реакции).

При р, Т = const для химической реакции верно:

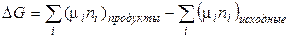. (2.55)

Расчёт химического потенциала:

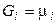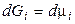1. Для 1 моля идеального газа.Для индивидуального вещества и , тогда при Т = const

dG = Vdp-SdT = Vdp, (2.56)

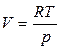и 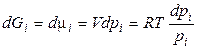, (2.57)

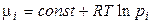, (2.58)

где р_i – давление индивидуального газа. Обычно const рассчитывают при Т = 298 К и р^o = 1,013·10⁵ Па, тогда

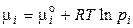. (2.59)

2. Для смеси идеальных газов:

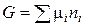
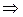
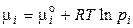, (2.60)

где р_i – парциальное давление i–го газа, и 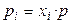, где 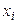– мольная доля i–го газа в смеси, p – общее давление в системе. Отсюда

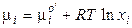. (2.61)

3. Для смеси реальных газов. С увеличением давления и понижением температуры газы всё больше становятся неидеальными, т. е. перестают подчиняться уравнению состояния идеального газа. Поэтому для реального газа в выражения химической термодинамики вместо парциального давления (р_i) подставляют летучесть (фугитивность f_i ). Численно летучесть выражается как 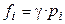, где γ – коэффициент летучести, характеризующий степень отклонения газа от идеальности. Тогда

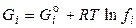, (2.62)

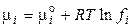. (2.63)

4. Для идеальных и реальных растворов. В неидеальных растворах концентрация перестаёт быть величиной, однозначно определяющей свойства раствора, поэтому концентрацию заменяют активностью. Введением активности формально учитывается взаимодействие между молекулами растворителя, эффект сольватации и т.п. Активность можно назвать эффективной концентрацией, при которой идеальный раствор приобретает термодинамические свойства данного реального раствора. Тогда: для идеальных растворов

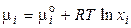; (2.64)

для реальных растворов

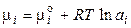, (2.65)

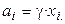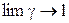где и при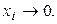

ЛЕКЦИЯ 3

Термодинамика химического равновесия. Константа химического равновесия. Закон действующих масс. Принцип Ле-Шателье. Изотерма химической реакции. Связь стандартного изменения энергии Гиббса реакции с константой равновесия. Равновесие в гетерогенных реакциях. Влияние температуры на химическое равновесие. Уравнения изобары и изохоры химической реакции.