ТЕПЛОЁМКОСТЬ. УРАВНЕНИЕ КИРХГОФА.

Теплоёмкость– то количество теплоты, которое необходимо сообщить или отнять телу или системе, чтобы их температура изменилась на 1 градус. Теплоёмкость — величина экстенсивная, так как зависит от размера системы. Теплоёмкость,рассчитанная на 1 моль вещества, называется мольной, а на единицу массы – удельной.

Различают:

— истинную теплоёмкость: 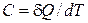[ 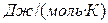]. (1.25)

— среднюю теплоёмкость: 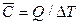. (1.26)

Наиболее часто используются следующие теплоемкости:

1. Изохорная теплоемкость. При нагреве или охлаждении вещества при постоянном объеме справедливо:

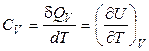. . (1.27)

2. Изобарная теплоемкость. При нагреве или охлаждении вещества при постоянном давлении справедливо:

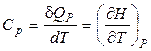. . (1.28)

Следует знать, что теплоёмкость при постоянном давлении С_р больше, чем теплоёмкость при постоянном объёме С_V, так как нагревание вещества при постоянном давлении сопровождается работой расширения, т.е.

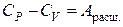. (1.29)

Для идеальных газов справедливо уравнение Майера:

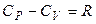. (1.30)

Величина R (универсальная газовая постоянная) равна работе расширения 1 моля идеального газа (при р = const) при увеличении его температуры на 1 градус.

Отношение 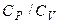обозначается символом 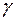(адиабатический коэффициент), который всегда больше нуля ( 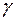> 0).

Зависимость теплоёмкости веществ в области не очень низких температур (Т ≥ 298 К) обычно выражается в виде следующих полиномов:

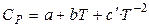. (1.31)

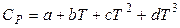. (1.32)

Значения a, b, c, c´, d приведены в справочниках физико-химических и термодинамических величин.

Рассмотрим уравнение Кирхгоффа, описывающее зависимость энтальпии реакции от температуры:

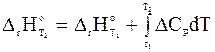, (1.33)

где

,

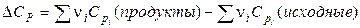т. е. разность между суммой теплоёмкостей продуктов реакции и исходных веществ с учётом стехиометрических коэффициентов.

Для вычисления интеграла необходимо знать зависимость теплоёмкости от температуры для всех веществ, что не всегда возможно. Поэтому уравнение Кирхгоффа применяют в трёх приближениях.

1. При наиболее грубом приближении полагают, что DС_p = 0, т.е. считают равными суммарные теплоёмкости продуктов и исходных веществ. Тогда ,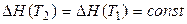

т.е. тепловой эффект считается не зависящим от температуры. Этим приближением пользуются, если теплоемкости некоторых участников реакции неизвестны.

2. Во втором приближении считают разность теплоёмкостей постоянной величиной DС_Р = const. Тогда

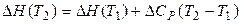. (1.34)

Это уравнение применяют только для небольшого интервала температур Т₂ – Т₁, в котором известны величины теплоёмкостей.

3. В наиболее точном приближении используют зависимость всех С_Рi от температуры. Если теплоемкости веществ даны в виде полиномов, например (1.34), то уравнение Кирхгоффа можно проинтегрировать, после чего оно будет иметь следующий вид:

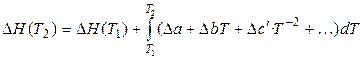. (1.35)

Последнее уравнение можно использовать только в том интервале температур Т₂ – Т₁, для которого определены коэффициенты a_i, b_i, c_i температурной зависимости теплоёмкостей веществ.

ЛЕКЦИЯ 2

Второй закон термодинамики. Энтропия. Вычисление изменения энтропии для различных процессов. Постулат Планка. Энергия Гиббса и энергия Гельмгольца. Уравнение Гиббса-Гельмгольца. Самопроизвольное протекание химических реакций. Расчет изменения энергии Гиббса в химических реакциях. Химический потенциал. Активность и летучесть.