Пример 1 проверки устойчивости инверсного фильтра.

Оператор фильтра h_n = {0.131, 0.229, 0.268, 0.211, 0.111, 0.039, 0.009, 0.001}, N = 7. Оценить возможность инверсии оператора.

1. Переводим значения оператора в полином по zⁿ: H(z) = S_n h_n zⁿ.

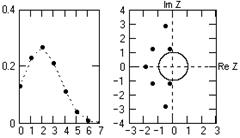Рис. 7.1.3.

2. Находим модули корней полинома: z_n = {1.896, 1.896, 1.896, 2.87, 2.87, 1.253, 1.253}.

Модули всех корней больше 1, следовательно, полюсы инверсного полинома будут находиться за пределами единичной окружности на z-плоскости, и инверсный оператор устойчив. Форма исходного оператора и положение полюсов инверсного оператора на z-плоскости приведены на рис. 7.1.3. Попутно отметим, что чем дальше от единичной окружности ближайшие к ней полюса, тем быстрее затухает инверсный оператор фильтра.

Пример 2 проверки устойчивости инверсного фильтра.

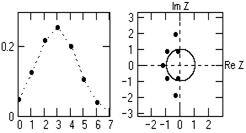Рис. 7.1.4.

Оператор фильтра h_n практически тот же самый, но сдвинут вправо на один отсчет и, соответственно, дополнен новым нулевым отсчетом h₀ = 0.048.

Находим новые модули корней полинома: z_n = {1.271, 1.271, 1.271, 1.924, 1.924, 0.84, 0.84}.

Форма исходного оператора и положение полюсов приведены на рис. 7.1.4. Два полюса находятся внутри единичного круга, а, следовательно, инверсный оператор не будет устойчивым (будет незатухающим расходящимся рядом).

Обращение недиракоидных функций. Если H(z) - реверсоид, т.е. корни составляющих его диполей находятся внутри и на единичном круге в z-плоскости, то устойчивое обращение H(z) является антиимпульсом (с отрицательными степенями z) и для его использования необходимо располагать "будущими" значениями входного сигнала.

Пример.

Передаточная функция фильтра: H(z) = 1-2z. Инверсная функция H^-1(z) = 1/(1-2z). Частотные спектры функций приведены на рис. 7.1.5.

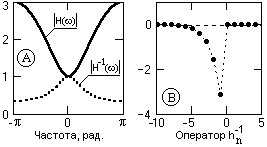Рис. 7.1.5.

Полюс функции z_p = 1/2 и находится внутри единичного круга на z-плоскости.

Перепишем выражение для инверсного фильтра в следующем виде:

H^-1(z) = -(1/2z) [1+1/2z+1/(2z)²+...].

Это выражение является разложением в ряд по степеням 1/z и сходится к кругу радиусом 1/2 при z → ¥. Коэффициенты при степенях 1/z являются, соответственно, коэффициентами инверсного фильтра с координатами (-n), т.е. фильтр оперирует с "будущими" отсчетами входного сигнала (см. рис. 7.1.5).

Если диполи функции (7.1.4) представляют собой и диракоиды, и реверсоиды, то обращение будет центроидом и определяется полным рядом Лорана:

H^-1(z) = ...+h_-2z^-2+h_-1z^-1+h₀+ h₁z¹+h₂z²+ ...,

т.е. оператор инверсного фильтра является двусторонним и не обязательно симметричным, как мы обычно рассматривали ранее двусторонние операторы.

7.2. Инверсия импульсного отклика фильтра.

Вычисление коэффициентов инверсного фильтра по значениям каузального (одностороннего) оператора h(n) может быть проведено на основе выражения (7.1.2):

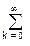h^-1(k)h(n-k) = d_o(n), (7.2.1)

для чего достаточно развернуть его в систему n-уравнений при n = 0,1,2…, k ≤ n

n = 0: h^-1(0)h(0) = 1, h^-1(0) = 1/h(0).

n = 1: h^-1(0)h(1)+h^-1(1)h(0) = 0, h^-1(1) = h^-1(0)h(1) / h(0).

n = 2: h^-1(0)h(2)+h^-1(1)h(1)+h^-1(2)h(0) = 0, h^-1(2) = (h^-1(0)h(2)+h^-1(1)h(1))/h(0), и т.д.

Продолжая последовательно, можно вычислить любое количество значений коэффициентов инверсного фильтра. Рекуррентная формула вычислений:

h^-1(n) = -[ 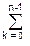h^-1(k)h(n-k)] / h(0). (7.2.2)

Если фильтр деконволюции устойчив и ряд h^-1(n) сходится, то появляется возможность разумного ограничения количества членов ряда с определенной ошибкой восстановления исходного сигнала. Метрика приближения Е (квадратичная норма разности) определяется выражением:

Е² = 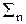[d_o(n) - h(n) _* h^-1(n)]². (7.2.3)

Ошибка восстановления исходного сигнала проявляется со сдвигом на длину прямого оператора фильтра.