Пример расчета полосового фильтра Баттеруорта.

Техническое задание:

- Шаг дискретизации данных Dt = 0.0005 сек.

Частота Найквиста f_N = 1/2Dt = 1000 Гц, ω_N = 6.283·10³ рад.

- Нижняя граничная частота полосы пропускания: f_н = 340 Гц, w_н = 2.136·10³ рад.

- Верхняя граничная частота полосы пропускания: f_в = 470 Гц, w_в = 2.953·10³ рад.

- Крутизна срезов в децибелах на октаву: К_р = 45.

Расчет параметров:

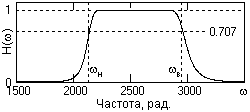Рис. 6.3.2.

1. Порядок фильтра по формуле (6.1.6'):

N = К_р/6 = 45/6 = 7.5.

Для расчетов принимаем N=8.

2. Строим график функции H(w) = 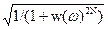с использованием выражения (6.3.7). Передаточная характеристика фильтра приведена на рис. 6.3.2.

3. Деформированные частоты по формуле (6.1.4):

w_dн = 2.366·10³ рад. w_dв = 3.64·10³ рад. w_do = 2.934·10³.

Полосовой фильтр на s-плоскости. С учетом деформации частот, принимаем p = jw = j(w²-w_dнw_dв)/[w(w_dв-w_dн)], s= jω и заменяем ω = s/j в выражении р:

р = (s²+w_dнw_dв)/[s(w_dв-w_dн)],

s²-p(w_dв-w_dн)s+w_dнw_dв = 0. (6.3.8)

Koрни уравнения (6.3.8) определяют местоположение полюсов ПФ:

s = s* = p(w_dв-w_dн)/2 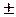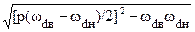. (6.3.9)

Уравнение (6.3.9) показывает расщепление каждого p-полюса, определяемых выражением (6.1.14), на два комплексно сопряженных полюса s-плоскости, произведение которых будет давать вещественные биквадратные блоки в s-плоскости. При этом следует учесть то обстоятельство, что устойчивому рекурсивному фильтру на z-плоскости должны соответствовать полюса только одной (левой) половины p,s - плоскостей.

Передаточная функция. При применении преобразования (6.3.1) к передаточной функции в полиномиальной форме (6.1.11), получаем:

H(p) = G 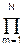1/(p-p_m) ó G 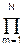s/(s²-p_m s+1) = H(s), (6.3.10)

Выражение (6.3.10) не требует нахождения полюсов, т.к. они уже известны и определяются выражением (6.3.9). С учетом этого функция H(s) может быть записана с объединением в биквадратные блоки комплексно сопряженных полюсов с вещественными коэффициентами:

H(s) = G 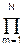s/[(s-s_m)(s-s*_m)] = G 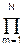s/(s²+a_m s+g_m), (6.3.11)

где значения а_m и g_m могут быть определены непосредственно по полюсам (6.3.9):

a_m = -2 Re s_m, g_m = (Re s_m)² + (Im s_m)² = |s_m|². (6.3.12)

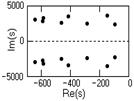Рис. 6.3.3. Рис. 6.3.4.