Пример инверсии оператора фильтра.
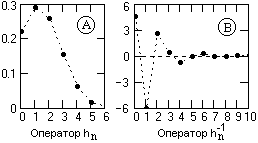 Рис. 7.2.1.
Рис. 7.2.1.
|
Оператор фильтра
hn = {0.219, 0.29, 0.257, 0.153, 0.061, 0.016, 0.003}.
1. Полином по zn: H(z) = Sn hn zn.
2. Модули корней полинома:
zn = {2.054, 2.054, 2.485, 2.485, 1.699, 1.699}.
Модули корней больше 1, инверсный фильтр должен быть устойчивым и, судя по значениям корней (достаточно существенно отличающимся от 1), быстро затухающим.
3. Двенадцать первых значений инверсного оператора при вычислении по (7.2.2):
h-1(n) = {4.56, -6.033, 2.632, 0.417, -0.698, -0.062, 0.267, -0.024, -0.11, 0.051, 0.018, -0.019, 0.004}.
Значения прямого и инверсного оператора фильтра приведены на рис. 7.2.1.
4. Значения свертки прямого оператора с инверсным при разной длине N инверсного фильтра и метрика приближения:
N=4, sn={1, 0, 0, 0, 0, 0.014, -0.04, -0.056, -0.028, -0.01, -0.002, 0, 0, …}. E=0.077.
N=6, sn={1, 0, 0, 0, 0, 0, 0, 0.005, 0.031, 0.027, 0.013, 0.004, 0.001, 0, 0, …}. E=0.044.
N=8, sn={1, 0, 0, 0, 0, 0, 0, 0, 0, -0.011, -0.019, -0.014, -0.006, 0.002, <0.001, 0, 0, …}. E=0.027.
N=10, sn={1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0.004, 0.006, 0.004, 0.002, <0.001, 0, 0, …}. E=0.0086.
На рис. 7.2.2 приведены абсолютные значения ошибки деконволюции при разной длине N.

Рис. 7.2.2.
7.3. Оптимальные фильтры деконволюции /л12,л22/.
Можно рассчитать оптимальные фильтры деконволюции, метрика приближения которых много меньше, чем у усеченных фильтров деконволюции. Для получения общего уравнения оптимальной деконволюции будем считать, что число коэффициентов оператора hn равно M+1, a число коэффициентов инверсного оператора hn-1 равно N+1.
Принцип оптимизации. Выходная функция приближения при использовании уравнения свертки (7.1.2) с ограничением числа членов оператора фильтра:
F = Е2 = 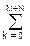 [do(k)-xk]2. xk =
[do(k)-xk]2. xk = 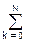 hn-1 hk-n. (7.3.1)
hn-1 hk-n. (7.3.1)
Чтобы определить минимум функции, приравняем нулю частные производные от Е по неизвестным коэффициентам фильтра:
dF/dhj-1 = 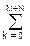 -2hk-j [do(k) -
-2hk-j [do(k) - 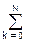 hn-1 hk-n] = 0. (7.3.2)
hn-1 hk-n] = 0. (7.3.2)
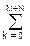 hk-j
hk-j 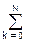 hn-1 hk-n =
hn-1 hk-n = 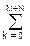 hk-j do(k) = h-j. (7.3.3)
hk-j do(k) = h-j. (7.3.3)
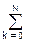 hn-1
hn-1 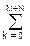 hk-n hk-j =
hk-n hk-j = 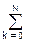 hn-1 aj-n = h-j, j = 0,1,2, ..., N, (7.3.4)
hn-1 aj-n = h-j, j = 0,1,2, ..., N, (7.3.4)
где aj-n - функция автоковариации импульсной реакции h(n). Учитывая также, что hn = 0 при n<0 и аj = a-j (функция автоковариации является четной функцией), окончательное решение определяется следующей системой линейных уравнений:
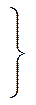 (7.3.5) (7.3.5)
|
a0 h0-1 + a1 h1-1 + a2 h2-1 + a3 h3-1 + ... + aN hN-1 = h0
a1 h0-1 + a0 h1-1 + a1 h2-1 + a2 h3-1 + ... + aN-1 hN-1 = 0
a2 h0-1 + a1 h1-1 + a0 h2-1 + a1 h3-1 + ... + aN-2 hN-1 = 0
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
aN h0-1 + aN-1 h1-1 + aN-2 h2-1 + aN-3 h3-1 +... +a0 hN-1 = 0
Дата добавления: 2020-02-05; просмотров: 707;











