Тема 7: ДЕКОНВОЛЮЦИЯ СИГНАЛОВ

Если дом красив, то мы понимаем, что он был выстроен для хозяев, а не для мышей.

Хрисипп (греческий философ).

Деконволюция сходна с археологией. Задача – восстановить дом из развалин. Обнадеживает, если все обломки на месте. Но если остался только песок, и для мышей дома не получится.

Григорий Старцев (Геофизик).

Содержание: 7.1. Понятие деконволюции. Определение деконволюции. Особенности деконволюции. Устойчивость фильтров деконволюции. 7.2. Инверсия импульсного отклика фильтра. 7.3. Оптимальные фильтры деконволюции. Принцип оптимизации. Уравнение оптимальной инверсии. Уравнение Левинсона. 7.4. Рекурсивная деконволюция. 7.5. Фильтры неполной деконволюции. Литература.

7.1. Понятие деконволюции.

Деконволюция или обратная свертка в геофизике используется очень широко. Она применяется для сжатия сигналов с целью повышения временного или пространственного разрешения результатов измерений. В грави- и магниторазведке с использованием деконволюции производятся перерасчеты аномальных полей вниз. В ядерной геофизике методы деконволюции являются основными при количественной интерпретации результатов измерений, чему способствует принцип суперпозиции ядерно-физических полей.

Определение деконволюции. Если для прямой свертки сигнала x(k) c импульсным откликом h(n) линейной системы (фильтра) мы имеем уравнение:

y(k) = h(n) _* x(k) ó H(z)X(z) = Y(z),

то, в принципе, возможна постановка и обратной задачи, задачи деконволюции - определение сигнала на входе линейной системы по значениям выходного сигнала:

X(z) = Y(z)/H(z) = Y(z)H^-1(z) ó y(k) _* h^-1(n) = x(k), (7.1.1)

где индексом "-1" символически обозначен оператор обратного фильтра, инверсный прямому. Очевидно:

H(z)H^-1(z) = 1 ó h(n) _* h^-1(n) = d_o(n), (7.1.2)

H^-1(z) = 1/H(z) ó h^-1(n). (7.1.3)

где d_o(n) - импульс Кронекера (d_o(n) = 1 при n = 0, d_o(n) = 0 при n ≠ 0).

Пример инверсии оператора через спектральное представление приведен на рис. 7.1.1 (исходный оператор h_n ® спектральная плотность H(ω) ® инверсная спектральная плотность H^-1(ω) ® инверсный оператор h^-1_n на начальном интервале отсчетов).

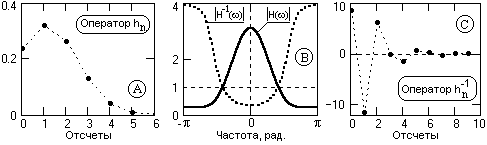Рис. 7.1.1.

Особенности деконволюции. Выражение (7.1.3) позволяет сделать некоторые выводы об особенностях выполнения деконволюции.

При ограниченной импульсной реакции h(n) инверсный оператор h^-1(n) в общем случае не ограничен. Так, например, если импульсная реакция представлена нормированным диполем h(n) = {1,a} ó (1+az) = h(z), то имеем:

H^-1(z) = 1/(1+az) = 1-az+a²z²-a³z³+ ....

h^-1(n) = {1, -a, a², -a³,....}.

Это действительно практически для любых операторов фильтров, энергия которых на каких-либо ограниченных участках главного частотного диапазона близка к нулевой. При инверсии спектральной функции таких операторов на этих участках возникают резкие энергетические пики, которые при обратном преобразовании Фурье дает медленно затухающие функции операторов. Пример такого явления приведен на рис. 7.1.2.

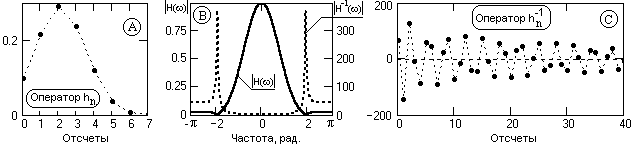Рис. 7.1.2.

Отсюда следует, что для точного выполнения деконволюции необходимо располагать бесконечно длинным инверсным оператором фильтра. Заметим также, что инверсия операторов обычно всегда связана с усилением высоких частот, что приводит к резкому повышению коэффициента усиления дисперсии помех инверсных фильтром. Практически, деконволюция выполняется, если инверсный оператор достаточно быстро затухает и может быть ограничен. Но использование усеченных операторов приводит к появлению определенной погрешности деконволюции, величину которой следует контролировать.

Устойчивость фильтров деконволюции. Функция H(z) в выражении (7.1.3) имеет особые точки - нули функции, которые становятся полюсами функции H^-1(z) = 1/H(z) и определяют устойчивость инверсного фильтра. Для того чтобы фильтр деконволюции был устойчивым, ряд 1/H(z) должен сходиться, т.е. полюса функции должны находиться вне единичного круга на z-плоскости.

Многочлен H(z) порядка N может быть разложен на N простых сомножителей - двучленов (диполей):

H(z) = (а-z)(b-z)(c-z)...., (7.1.4)

где а, b, с,.. - корни полинома. Обращение передаточной функции:

H^-1(z) = (7.1.5)

Если каждый из диполей функции (7.1.4) является минимально-фазовым диракоидом, т.е. корни диполей находится вне единичного круга на z-плоскости и модули нулевых членов диполей всегда больше следующих за ними первых членов (в данном случае: |а|>1, |b|>1, |с|>1), то и функция H(z) в целом также является минимально-фазовым диракоидом. При этом максимум энергии импульсного отклика сосредоточен в его начальной части и последовательность отсчетов представляет собой затухающий ряд. Соответственно, и функция 1/H(z) также будет представлять собой сходящийся ряд, и инверсный фильтр будет устойчив. Так, например, фильтр, реализующий передаточную функцию (7.1.5), в самой общей форме может быть выполнен в виде включенных последовательно фильтров, каждый из которых имеет передаточную функцию следующего типа (для первого фильтра):

H₁^-1(z) = 1/(a-z) = (1+z/a+z²/a²+...)/a.